Bayesian multivariate linear regression
Encyclopedia
In statistics
, Bayesian multivariate linear regression is a Bayesian
approach to multiple linear regression
.
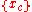, and a jointly normal errors 
:
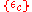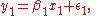
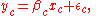
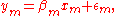
where the subscript c denotes a column vector of k observations for each measurement
(
).
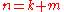The noise terms are jointly normal over each collection of k observations. That is, each row vector
represents an m length vector of correlated observations on each of the dependent variables:
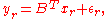
where the noise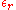
is i.i.d. and normally distributed for all rows 
.
where B is an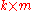
matrix
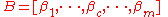
We can write the entire regression problem in matrix form as:
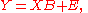
where Y and E are
matrices.
The classical, frequentists linear least squares
solution is to simply estimate the matrix of regression coefficients
using the Moore-Penrose pseudoinverse
:
.
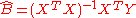To obtain the Bayesian solution, we need to specify the conditional likelihood and then find the appropriate conjugate prior. As with the univariate case of linear Bayesian regression
, we will find that we can specify a natural conditional conjugate prior (which is scale dependent).
Let us write our conditional likelihood as
writing the error E in terms Y,X, and B yields
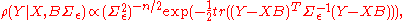
We seek a natural conjugate prior—a joint density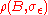
which is of the same functional form as the likelihood. Since the likelihood is quadratic in 
, we re-write the likelihood so it is normal in 
(the deviation from classical sample estimate)
Using the same technique as with Bayesian linear regression
, we decompose the exponential term using a matrix-form of the sum-of-squares technique. Here, however, we will also need to use the Matrix Differential Calculus (Kronecker product
and vectorization
transformations).
First, let us apply sum-of-squares to obtain new expression for the likelihood:
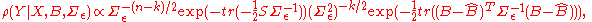
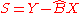
We would like to develop a conditional form for the priors:
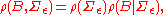
where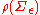
is an inverse-Wishart distribution
and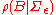
is some form of normal distribution in the matrix 
. This is accomplished using the vectorization
transformation, which converts the likelihood from a function of the matrices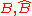
to a function of the vectors 
.
Write
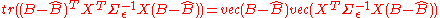
Let
Then
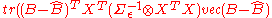
which will lead to a likelihood which is normal in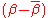
.
With the likelihood in a more tractable form, we can now find a natural (conditional) conjugate prior.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, Bayesian multivariate linear regression is a Bayesian
Bayesian
Bayesian refers to methods in probability and statistics named after the Reverend Thomas Bayes , in particular methods related to statistical inference:...
approach to multiple linear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
.
Details
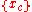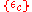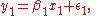
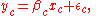
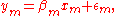
Consider a collection of m linear regression problems for n observations, related through a set of common predictor variables, and a jointly normal errors :where the subscript c denotes a column vector of k observations for each measurement
(
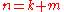).The noise terms are jointly normal over each collection of k observations. That is, each row vector
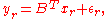
represents an m length vector of correlated observations on each of the dependent variables:where the noise
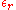is i.i.d. and normally distributed for all rows .where B is an
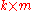matrix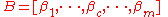We can write the entire regression problem in matrix form as:
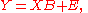
where Y and E are
matrices.The classical, frequentists linear least squares
Linear least squares
In statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model...
solution is to simply estimate the matrix of regression coefficients
using the Moore-Penrose pseudoinversePseudoinverse
In mathematics, and in particular linear algebra, a pseudoinverse of a matrix is a generalization of the inverse matrix. The most widely known type of matrix pseudoinverse is the Moore–Penrose pseudoinverse, which was independently described by E. H. Moore in 1920, Arne Bjerhammar in 1951 and...
:
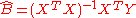.To obtain the Bayesian solution, we need to specify the conditional likelihood and then find the appropriate conjugate prior. As with the univariate case of linear Bayesian regression
Bayesian linear regression
In statistics, Bayesian linear regression is an approach to linear regression in which the statistical analysis is undertaken within the context of Bayesian inference...
, we will find that we can specify a natural conditional conjugate prior (which is scale dependent).
Let us write our conditional likelihood as
writing the error E in terms Y,X, and B yields
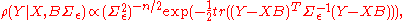
We seek a natural conjugate prior—a joint density
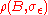which is of the same functional form as the likelihood. Since the likelihood is quadratic in , we re-write the likelihood so it is normal in (the deviation from classical sample estimate)Using the same technique as with Bayesian linear regression
Bayesian linear regression
In statistics, Bayesian linear regression is an approach to linear regression in which the statistical analysis is undertaken within the context of Bayesian inference...
, we decompose the exponential term using a matrix-form of the sum-of-squares technique. Here, however, we will also need to use the Matrix Differential Calculus (Kronecker product
Kronecker product
In mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix...
and vectorization
Vectorization
Vectorization, in parallel computing, is a special case of parallelization, in which software programs that by default perform one operation at a time on a single thread are modified to perform multiple operations simultaneously....
transformations).
First, let us apply sum-of-squares to obtain new expression for the likelihood:
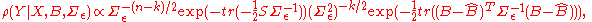
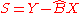
We would like to develop a conditional form for the priors:
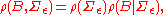
where
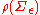is an inverse-Wishart distributionand
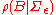is some form of normal distribution in the matrix . This is accomplished using the vectorizationVectorization
Vectorization, in parallel computing, is a special case of parallelization, in which software programs that by default perform one operation at a time on a single thread are modified to perform multiple operations simultaneously....
transformation, which converts the likelihood from a function of the matrices
to a function of the vectors .Write
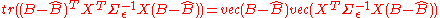
Let
Then
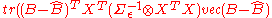
which will lead to a likelihood which is normal in
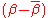.With the likelihood in a more tractable form, we can now find a natural (conditional) conjugate prior.