
Marginal likelihood
Encyclopedia
In statistics
, a marginal likelihood function, or integrated likelihood, is a likelihood function
in which some parameter variables have been marginalised. It may also be referred to as evidence, but this usage is somewhat idiosyncratic.
Given a parameter θ=(ψ,λ), where ψ is the parameter of interest, it is often desirable to consider the likelihood function only in terms of ψ. If there exists a probability distribution for λ, sometimes referred to as the nuisance parameter, in terms of ψ, then it may be possible to marginalise or integrate out λ: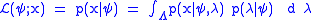
Unfortunately, marginal likelihoods are generally difficult to compute. Exact solutions are known for a small class of distributions. In general, some kind of numerical integration
method is needed, either a general method such as Gaussian integration or a Monte Carlo method
, or a method specialized to statistical problems such as the Laplace approximation, Gibbs sampling
or the EM algorithm.
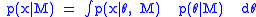
This quantity is important because the posterior odds ratio for a model M1 against another model M2 involves a ratio of marginal likelihoods, the so-called Bayes factor
:

which can be stated schematically as
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a marginal likelihood function, or integrated likelihood, is a likelihood function
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
in which some parameter variables have been marginalised. It may also be referred to as evidence, but this usage is somewhat idiosyncratic.
Given a parameter θ=(ψ,λ), where ψ is the parameter of interest, it is often desirable to consider the likelihood function only in terms of ψ. If there exists a probability distribution for λ, sometimes referred to as the nuisance parameter, in terms of ψ, then it may be possible to marginalise or integrate out λ:
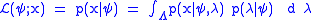
Unfortunately, marginal likelihoods are generally difficult to compute. Exact solutions are known for a small class of distributions. In general, some kind of numerical integration
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
method is needed, either a general method such as Gaussian integration or a Monte Carlo method
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
, or a method specialized to statistical problems such as the Laplace approximation, Gibbs sampling
Gibbs sampling
In statistics and in statistical physics, Gibbs sampling or a Gibbs sampler is an algorithm to generate a sequence of samples from the joint probability distribution of two or more random variables...
or the EM algorithm.
Bayesian model comparison
In Bayesian model comparison, the marginalized variables are parameters for a particular type of model, and the remaining variable is the identity of the model itself. In this case, the marginalized likelihood is the probability of the data given the model type, not assuming any particular model parameters. Writing θ for the model parameters, the marginal likelihood for the model M is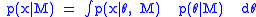
This quantity is important because the posterior odds ratio for a model M1 against another model M2 involves a ratio of marginal likelihoods, the so-called Bayes factor
Bayes factor
In statistics, the use of Bayes factors is a Bayesian alternative to classical hypothesis testing. Bayesian model comparison is a method of model selection based on Bayes factors.-Definition:...
:

which can be stated schematically as
- posterior oddsOdds ratioThe odds ratio is a measure of effect size, describing the strength of association or non-independence between two binary data values. It is used as a descriptive statistic, and plays an important role in logistic regression...
= prior odds × Bayes factorBayes factorIn statistics, the use of Bayes factors is a Bayesian alternative to classical hypothesis testing. Bayesian model comparison is a method of model selection based on Bayes factors.-Definition:...
See also
- Empirical Bayes methods
- Marginal probability

