Ballistic conduction
Encyclopedia
Ballistic conduction is the unimpeded flow of charge or energy carrying particles over relatively long distances in a material. Normally, transport of electrons (or holes) is dominated by scattering events, which relax the carrier momentum in an effort to bring the conducting material to equilibrium. Thus, ballistic transport in a material is determined by how ballistically conductive that material is. Ballistic conduction differs from superconductivity
due to the absence of the Meissner effect
in the material. A ballistic conductor would stop conducting if the driving force is turned off, whereas in a superconductor current would continue to flow after the driving supply is disconnected.
Ballistic conduction is typically observed in quasi-1D structures, such as carbon nanotubes or silicon nanowire
s, because of extreme size quantization effects in these materials. Ballistic conduction is not limited to electrons (or holes) but can also apply to phonons. It is theoretically possible for ballistic conduction to be extended to other quasi-particles, but this has not been experimentally verified.
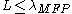where 
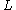is the length of the active part of the device (i.e., a channel in a MOSFET
).
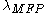is the mean scattering length for the carrier which can be given by Matthiessen's Rule
, written here for electrons:
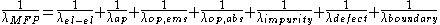
where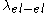
is the electron-electron scattering length, 
is the acoustic phonon (emission and absorption) scattering length, 
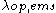is the optical phonon emission scattering length, 
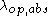is the optical phonon absorption scattering length, 
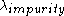is the electron-impurity scattering length, 
is the electron-defect scattering length,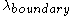 
is the electron scattering length with the boundary, and 
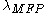is the total electron mean free path (electron scattering length). In terms of scattering mechanisms, optical phonon emission normally dominates, depending on the material and transport conditions. There are also other scattering mechanisms which apply to different carriers that are not considered here (e.g. remote interface phonon scattering, umklapp scattering
). To get these characteristic scattering rates, one would need to derive a Hamiltonian
and solve Fermi's Golden Rule
for the system in question.
proposed that conduction in a 1D system could be viewed as transmission problem. For the 1D GNRFET on the right (where the graphene nanoribbon channel is assumed to be ballistic), the current from A to B (given by the Boltzmann transport equation) is
where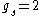
due to spin degeneracy, e is the electron charge, h=Planck's constant, 
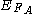and 
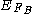are the Fermi levels of A and B, 
is the modes, 
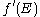is the deviation from the equilibrium electron distribution (perturbation), and 
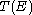is the transmission probability (T=1 for ballistic). Based on the definition of conductance
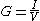and the voltage separation between the Fermi levels is approximately 
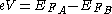, it follows that
where M is the number of modes in the transmission channel and spin is included.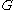 
is known as the quantized conductance
. The contacts have a multiplicity of modes due to their larger size in comparison to the channel. Conversely, the quantum confinement in the 1D GNR
channel constricts the number of modes to carrier degeneracy and restrictions from the material's energy dispersion relationship
and Brillouin zone
. For example, electrons in carbon nanotubes have two intervalley modes and two spin modes. Since the contacts and the GNR
channel are connected by leads, the transmission probability is smaller at contacts A and B,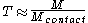
. Thus the quantum conductance is approximately the same if measured at A and B or C and D.
Landauer-Buttiker formalism holds as long as the carriers are coherent
(which means the length of the active channel is less than the phase-breaking mean free path) and the transmission functions can calculated from Schrödinger's equation
or approximated by the WKB approximation
. Therefore, even in the case of a perfect ballistic transport, there is a fundamental ballistic conductance which saturates the current of the device with a resistance of approximately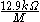
(spin degeneracy included).
There is, however, a generalization of the Landauer-Büttiker formalism of transport applicable to time-dependent problems in the presence of dissipation
.
properties of electron wave functions. Ballistic transport is coherent in wave mechanics
terms. Phenomena like double-split interference
, spacial resonance
(and other optical or microwave
-like effects) could be exploited in electronic systems at nanoscale.
Ballistic electrons behave like light in a waveguide
or a high-quality optical assembly. Non-ballistic electrons behave like light diffused in milk or reflected off a white wall or a piece of paper.
Electrons can be scattered several ways in a conductor. Electrons have several properties: wavelength (~energy), direction, phase, and spin orientation. Different materials have different scattering probabilities which cause different incoherence rates (stochasticity). Some kinds of scattering can only cause a change in electron direction, others can cause energy loss.
Consider a coherent source of electrons (like a laser
) connected to a conductor. Over a limited distance, the electron wave function will remain coherent. You still can deterministically predict its behavior (and use it for computation theoretically). After some greater distance, scattering causes each electron to have a slightly different phase
and/or direction. But there is still almost no energy loss. Like monochromatic light passing through milk, electrons undergo elastic
interactions. Information about the state of the electrons at the input is then lost. Transport becomes statistical and stochastic
. From the resistance point of view, stochastic (not oriented) movement of electrons is useless even if they carry the same energy - they move thermally. If the electrons undergo inelastic
interactions too, they lose energy and the result is a second mechanism of resistance. Electrons which undergo inelastic interaction are then similar to non-monochromatic light.
For correct usage of this analogy consideration of several facts is needed:
Thus this analogy is good only for single-electron conduction because electron processes are strongly and nonlinear dependent on other electrons.
or graphene nanoribbons
are often considered ballistic, but these devices only very closely resemble ballistic conduction. Their ballisticity is nearly 0.9 at room temperature.
mechanism at room temperature is that of electrons emitting optical phonons. If electrons don't scatter with enough phonons (for example if the scattering rate is low), the mean free path tends to be very long (
m). So a nanotube
or graphene nanoribbon could be a good ballistic conductor if the electrons in transit don't scatter with too many phonons and if the device is about 100 nm long.
s are quantum confined ballistic conductors. There are major differences between carbon nanotubes (which are hollow) and Si nanowires (which are solid). Nanowires are about 20-50 nm in diameter and are 3D solid while carbon nanotubes have diameters around the wavelength of an electron (2-3 nm) and are essentially 1D conductors. However it is still possible to observe ballistic conduction in Si nanowires at very low temperatures (2-3 K).
Superconductivity
Superconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...
due to the absence of the Meissner effect
Meissner effect
The Meissner effect is the expulsion of a magnetic field from a superconductor during its transition to the superconducting state. The German physicists Walther Meissner and Robert Ochsenfeld discovered the phenomenon in 1933 by measuring the magnetic field distribution outside superconducting tin...
in the material. A ballistic conductor would stop conducting if the driving force is turned off, whereas in a superconductor current would continue to flow after the driving supply is disconnected.
Ballistic conduction is typically observed in quasi-1D structures, such as carbon nanotubes or silicon nanowire
Nanowire
A nanowire is a nanostructure, with the diameter of the order of a nanometer . Alternatively, nanowires can be defined as structures that have a thickness or diameter constrained to tens of nanometers or less and an unconstrained length. At these scales, quantum mechanical effects are important —...
s, because of extreme size quantization effects in these materials. Ballistic conduction is not limited to electrons (or holes) but can also apply to phonons. It is theoretically possible for ballistic conduction to be extended to other quasi-particles, but this has not been experimentally verified.
Scattering mechanisms
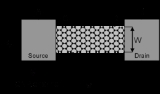
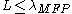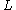In general, carriers will exhibit ballistic conduction when where is the length of the active part of the device (i.e., a channel in a MOSFETMOSFET
The metal–oxide–semiconductor field-effect transistor is a transistor used for amplifying or switching electronic signals. The basic principle of this kind of transistor was first patented by Julius Edgar Lilienfeld in 1925...
).
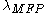is the mean scattering length for the carrier which can be given by Matthiessen's RuleAugustus Matthiessen
Augustus Matthiessen, FRS , the son of a merchant, was a British chemist and physicist who obtained his PhD in Germany at the University of Gießen in 1852 with Johann Heinrich Buff. He then worked with Robert Bunsen at the University of Heidelberg from 1853 to 1856...
, written here for electrons:
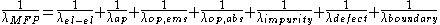
where
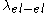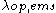is the electron-electron scattering length, is the acoustic phonon (emission and absorption) scattering length, is the optical phonon emission scattering length, 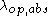is the optical phonon absorption scattering length, 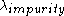is the electron-impurity scattering length, is the electron-defect scattering length, 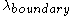is the electron scattering length with the boundary, and 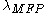is the total electron mean free path (electron scattering length). In terms of scattering mechanisms, optical phonon emission normally dominates, depending on the material and transport conditions. There are also other scattering mechanisms which apply to different carriers that are not considered here (e.g. remote interface phonon scattering, umklapp scatteringUmklapp scattering
Umklapp scattering is the transformation, like a reflection or a translation, of a wave vector to another Brillouin zone as a result of a scattering process, for example an electron-lattice potential scattering or an anharmonic phonon-phonon scattering process, reflecting an electronic state or...
). To get these characteristic scattering rates, one would need to derive a Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
and solve Fermi's Golden Rule
Fermi's golden rule
In quantum physics, Fermi's golden rule is a way to calculate the transition rate from one energy eigenstate of a quantum system into a continuum of energy eigenstates, due to a perturbation....
for the system in question.
Landauer-Buttiker formalism
In 1957, Rolf LandauerRolf Landauer
Rolf William Landauer was an IBM physicist who in 1961 argued that when information is lost in an irreversible circuit, the information becomes entropy and an associated amount of energy is dissipated as heat...
proposed that conduction in a 1D system could be viewed as transmission problem. For the 1D GNRFET on the right (where the graphene nanoribbon channel is assumed to be ballistic), the current from A to B (given by the Boltzmann transport equation) is
where
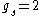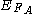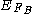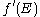due to spin degeneracy, e is the electron charge, h=Planck's constant, and are the Fermi levels of A and B, is the modes, is the deviation from the equilibrium electron distribution (perturbation), and 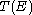is the transmission probability (T=1 for ballistic). Based on the definition of conductance 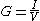and the voltage separation between the Fermi levels is approximately 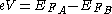, it follows that where M is the number of modes in the transmission channel and spin is included. 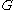is known as the quantized conductanceConductance quantum
The conductance quantum is the quantized unit of conductance. It is defined as G0 = 2e2/h = ≈ Ω−1. It appears when measuring the conductance of a quantum point contact....
. The contacts have a multiplicity of modes due to their larger size in comparison to the channel. Conversely, the quantum confinement in the 1D GNR
Graphene nanoribbons
Graphene nanoribbons , often abbreviated GNRs, are thin strips of graphene or unrolled single-walled carbon nanotubes...
channel constricts the number of modes to carrier degeneracy and restrictions from the material's energy dispersion relationship
Band diagram
This article refers to the electronic bandgap found in the semiconductors; for discussion of the photonic band gap, see Photonic Crystal article....
and Brillouin zone
Brillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
. For example, electrons in carbon nanotubes have two intervalley modes and two spin modes. Since the contacts and the GNR
Graphene nanoribbons
Graphene nanoribbons , often abbreviated GNRs, are thin strips of graphene or unrolled single-walled carbon nanotubes...
channel are connected by leads, the transmission probability is smaller at contacts A and B,
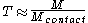. Thus the quantum conductance is approximately the same if measured at A and B or C and D.Landauer-Buttiker formalism holds as long as the carriers are coherent
Coherence (physics)
In physics, coherence is a property of waves that enables stationary interference. More generally, coherence describes all properties of the correlation between physical quantities of a wave....
(which means the length of the active channel is less than the phase-breaking mean free path) and the transmission functions can calculated from Schrödinger's equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
or approximated by the WKB approximation
WKB approximation
In mathematical physics, the WKB approximation or WKB method is a method for finding approximate solutions to linear partial differential equations with spatially varying coefficients...
. Therefore, even in the case of a perfect ballistic transport, there is a fundamental ballistic conductance which saturates the current of the device with a resistance of approximately
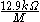(spin degeneracy included).There is, however, a generalization of the Landauer-Büttiker formalism of transport applicable to time-dependent problems in the presence of dissipation
Dissipation
In physics, dissipation embodies the concept of a dynamical system where important mechanical models, such as waves or oscillations, lose energy over time, typically from friction or turbulence. The lost energy converts into heat, which raises the temperature of the system. Such systems are called...
.
Importance of ballistic conductivity
Ballistic conduction enables use of quantum mechanicalQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
properties of electron wave functions. Ballistic transport is coherent in wave mechanics
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
terms. Phenomena like double-split interference
Double-slit experiment
The double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
, spacial resonance
Resonance
In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
(and other optical or microwave
Microwave
Microwaves, a subset of radio waves, have wavelengths ranging from as long as one meter to as short as one millimeter, or equivalently, with frequencies between 300 MHz and 300 GHz. This broad definition includes both UHF and EHF , and various sources use different boundaries...
-like effects) could be exploited in electronic systems at nanoscale.
Optical analogies of ballistic conduction
A comparison with light provides an analogy between ballistic and non-ballistic conduction.Ballistic electrons behave like light in a waveguide
Waveguide
A waveguide is a structure which guides waves, such as electromagnetic waves or sound waves. There are different types of waveguides for each type of wave...
or a high-quality optical assembly. Non-ballistic electrons behave like light diffused in milk or reflected off a white wall or a piece of paper.
Electrons can be scattered several ways in a conductor. Electrons have several properties: wavelength (~energy), direction, phase, and spin orientation. Different materials have different scattering probabilities which cause different incoherence rates (stochasticity). Some kinds of scattering can only cause a change in electron direction, others can cause energy loss.
Consider a coherent source of electrons (like a laser
Laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...
) connected to a conductor. Over a limited distance, the electron wave function will remain coherent. You still can deterministically predict its behavior (and use it for computation theoretically). After some greater distance, scattering causes each electron to have a slightly different phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
and/or direction. But there is still almost no energy loss. Like monochromatic light passing through milk, electrons undergo elastic
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
interactions. Information about the state of the electrons at the input is then lost. Transport becomes statistical and stochastic
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
. From the resistance point of view, stochastic (not oriented) movement of electrons is useless even if they carry the same energy - they move thermally. If the electrons undergo inelastic
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
interactions too, they lose energy and the result is a second mechanism of resistance. Electrons which undergo inelastic interaction are then similar to non-monochromatic light.
For correct usage of this analogy consideration of several facts is needed:
- Photons are bosons and electrons are fermions.
- There is coulombic repulsionCoulomb's lawCoulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
between electrons.
Thus this analogy is good only for single-electron conduction because electron processes are strongly and nonlinear dependent on other electrons.
- It is more likely that an electron would lose energy than a photon would, because of the electron's non-zero rest mass.
- Electron interactions with the environment, each other, and other particles are generally stronger than interactions with and between photons.
Examples of ballistic conduction
As mentioned, nanostructures such as carbon nanotubesBallistic Conduction in Single-Walled Carbon Nanotubes
- Conductance Quantization and Landauer Formula :Conduction in single-walled carbon nanotubes is quantized due to their one-dimensionality and the number of allowed electronic states is limited, if compared to bulk graphite. The nanotubes behave consequently as quantum wires and charge carriers are...
or graphene nanoribbons
Graphene nanoribbons
Graphene nanoribbons , often abbreviated GNRs, are thin strips of graphene or unrolled single-walled carbon nanotubes...
are often considered ballistic, but these devices only very closely resemble ballistic conduction. Their ballisticity is nearly 0.9 at room temperature.
Carbon nanotubes and graphene nanoribbon
The dominant scatteringScattering
Scattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...
mechanism at room temperature is that of electrons emitting optical phonons. If electrons don't scatter with enough phonons (for example if the scattering rate is low), the mean free path tends to be very long (
m). So a nanotubeCarbon nanotube
Carbon nanotubes are allotropes of carbon with a cylindrical nanostructure. Nanotubes have been constructed with length-to-diameter ratio of up to 132,000,000:1, significantly larger than for any other material...
or graphene nanoribbon could be a good ballistic conductor if the electrons in transit don't scatter with too many phonons and if the device is about 100 nm long.
Si nanowires
It is often incorrectly thought that Si nanowireNanowire
A nanowire is a nanostructure, with the diameter of the order of a nanometer . Alternatively, nanowires can be defined as structures that have a thickness or diameter constrained to tens of nanometers or less and an unconstrained length. At these scales, quantum mechanical effects are important —...
s are quantum confined ballistic conductors. There are major differences between carbon nanotubes (which are hollow) and Si nanowires (which are solid). Nanowires are about 20-50 nm in diameter and are 3D solid while carbon nanotubes have diameters around the wavelength of an electron (2-3 nm) and are essentially 1D conductors. However it is still possible to observe ballistic conduction in Si nanowires at very low temperatures (2-3 K).