
Autoregressive fractionally integrated moving average
Encyclopedia
In statistics
, autoregressive fractionally integrated moving average models are time series
models that generalize ARIMA
(autoregressive integrated moving average) models by allowing non-integer values of the differencing parameter
and are useful in modeling time series with long memory. The acronym "ARFIMA" is sometimes used, although it is conventional to simply extend the "ARIMA(p,d,q)" notation for models, by simply allowing the order of differencing, d, to take fractional values.
model, the integrated part of the model includes the differencing operator, in terms of the backspace operator B, as an integer power of (1 − B). For example
where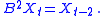
In a fractional model, the power is allowed to be fractional, with the meaning of the term identified using the following formal binomial series
expansion

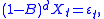
where this has the interpretation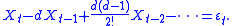
ARFIMA(0,d,0) is similar to fractional Gaussian noise (fGn): with d = H−½, their covariances have the same power-law decay. The advantage of fGn over ARFIMA(0,d,0) is that many asymptotic relations hold for finite samples. The advantage of ARFIMA(0,d,0) over fGn is that it has an especially simple spectral density
—
—and it is a particular case of ARFIMA(p,d,q), which is a versatile family of models.
(p,d,q) process, specifically:
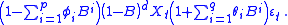
In contrast to the ordinary ARIMA process, the "difference parameter", d, is allowed to take non-integer values.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, autoregressive fractionally integrated moving average models are time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
models that generalize ARIMA
Arima
The Royal Borough of Arima is the fourth largest town in Trinidad and Tobago. Located east of the capital, Port of Spain, Arima supports the only organised indigenous community in the country, the Santa Rosa Carib Community and is the seat of the Carib Queen...
(autoregressive integrated moving average) models by allowing non-integer values of the differencing parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
and are useful in modeling time series with long memory. The acronym "ARFIMA" is sometimes used, although it is conventional to simply extend the "ARIMA(p,d,q)" notation for models, by simply allowing the order of differencing, d, to take fractional values.
Basics
In an ARIMAArima
The Royal Borough of Arima is the fourth largest town in Trinidad and Tobago. Located east of the capital, Port of Spain, Arima supports the only organised indigenous community in the country, the Santa Rosa Carib Community and is the seat of the Carib Queen...
model, the integrated part of the model includes the differencing operator, in terms of the backspace operator B, as an integer power of (1 − B). For example

where
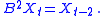
In a fractional model, the power is allowed to be fractional, with the meaning of the term identified using the following formal binomial series
Binomial series
In mathematics, the binomial series is the Taylor series at x = 0 of the function f given by f = α, where is an arbitrary complex number...
expansion

ARFIMA(0,d,0)
The simplest autoregressive fractionally integrated model, ARFIMA(0,d,0), is, in standard notation,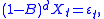
where this has the interpretation
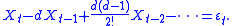
ARFIMA(0,d,0) is similar to fractional Gaussian noise (fGn): with d = H−½, their covariances have the same power-law decay. The advantage of fGn over ARFIMA(0,d,0) is that many asymptotic relations hold for finite samples. The advantage of ARFIMA(0,d,0) over fGn is that it has an especially simple spectral density
Spectral density
In statistical signal processing and physics, the spectral density, power spectral density , or energy spectral density , is a positive real function of a frequency variable associated with a stationary stochastic process, or a deterministic function of time, which has dimensions of power per hertz...
—
- f(λ) = (1/2π) (2sin(λ/2))−2d
—and it is a particular case of ARFIMA(p,d,q), which is a versatile family of models.
General form: ARFIMA(p,d,q)
An ARFIMA model shares the same form of representation as the ARIMAArima
The Royal Borough of Arima is the fourth largest town in Trinidad and Tobago. Located east of the capital, Port of Spain, Arima supports the only organised indigenous community in the country, the Santa Rosa Carib Community and is the seat of the Carib Queen...
(p,d,q) process, specifically:
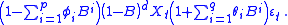
In contrast to the ordinary ARIMA process, the "difference parameter", d, is allowed to take non-integer values.
See also
- Fractional calculusFractional calculusFractional calculus is a branch of mathematical analysis that studies the possibility of taking real number powers or complex number powers of the differentiation operator.and the integration operator J...
— fractional differentiation - Differintegral — fractional integration and differentiation
- Fractional Brownian motion — a continuous-time stochastic process with a similar basis
- Long-range dependencyLong-range dependencyLong-range dependency is a phenomenon that may arise in the analysis of spatial or time series data. It relates to the rate of decay of statistical dependence, with the implication that this decays more slowly than an exponential decay, typically a power-like decay...

