
Selberg sieve
Encyclopedia
In mathematics
, in the field of number theory
, the Selberg sieve is a technique for estimating the size of "sifted sets" of positive integers which satisfy a set of conditions which are expressed by congruences. It was developed by Atle Selberg
in the 1940s.
the Selberg sieve is of combinatorial type: that is, derives from a careful use of the inclusion-exclusion principle
. Selberg replaced the values of the Möbius function
which arise in this by a system of weights which are then optimised to fit the given problem. The result gives an upper bound for the size of the sifted set.
Let A be a set of positive integers ≤ x and let P be a set of primes. For each p in P, let Ap denote the set of elements of A divisible by p and extend this to let Ad the intersection of the Ap for p dividing d, when d is a product of distinct primes from P. Further let A1 denote A itself. Let z be a positive real number and P(z) denote the product of the primes in P which are ≤ z. The object of the sieve is to estimate
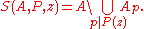
We assume that |Ad| may be estimated by
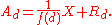
where f is a multiplicative function
and X = |A|. Let the function g be obtained from f by Möbius inversion
, that is
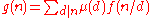

where μ is the Möbius function
.
Put

Then
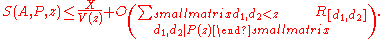
It is often useful to estimate V(z) by the bound
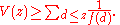
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the Selberg sieve is a technique for estimating the size of "sifted sets" of positive integers which satisfy a set of conditions which are expressed by congruences. It was developed by Atle Selberg
Atle Selberg
Atle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
in the 1940s.
Description
In terms of sieve theorySieve theory
Sieve theory is a set of general techniques in number theory, designed to count, or more realistically to estimate the size of, sifted sets of integers. The primordial example of a sifted set is the set of prime numbers up to some prescribed limit X. Correspondingly, the primordial example of a...
the Selberg sieve is of combinatorial type: that is, derives from a careful use of the inclusion-exclusion principle
Inclusion-exclusion principle
In combinatorics, the inclusion–exclusion principle is an equation relating the sizes of two sets and their union...
. Selberg replaced the values of the Möbius function
Möbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
which arise in this by a system of weights which are then optimised to fit the given problem. The result gives an upper bound for the size of the sifted set.
Let A be a set of positive integers ≤ x and let P be a set of primes. For each p in P, let Ap denote the set of elements of A divisible by p and extend this to let Ad the intersection of the Ap for p dividing d, when d is a product of distinct primes from P. Further let A1 denote A itself. Let z be a positive real number and P(z) denote the product of the primes in P which are ≤ z. The object of the sieve is to estimate
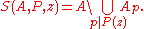
We assume that |Ad| may be estimated by
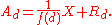
where f is a multiplicative function
Multiplicative function
In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
and X = |A|. Let the function g be obtained from f by Möbius inversion
Möbius inversion formula
In mathematics, the classic Möbius inversion formula was introduced into number theory during the 19th century by August Ferdinand Möbius. Other Möbius inversion formulas are obtained when different local finite partially ordered sets replace the classic case of the natural numbers ordered by...
, that is
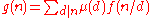

where μ is the Möbius function
Möbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
.
Put

Then
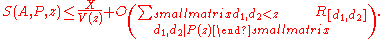
It is often useful to estimate V(z) by the bound
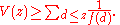
Applications
- The Brun–Titchmarsh theoremBrun–Titchmarsh theoremIn analytic number theory, the Brun–Titchmarsh theorem, named after Viggo Brun and Edward Charles Titchmarsh, is an upper bound on the distribution of prime numbers in arithmetic progression...
on the number of primes in arithmetic progressionPrimes in arithmetic progressionIn number theory, the phrase primes in arithmetic progression refers to at least three prime numbers that are consecutive terms in an arithmetic progression, for example the primes ....
; - The number of n ≤ x such that n is coprime to φ(n) is asymptotic to e−γ x / log log log (x) .

