Artin-Schreier theory
Encyclopedia
In mathematics
, Artin–Schreier theory is a branch of Galois theory
, and more specifically is a positive characteristic
analogue of Kummer theory
, for Galois extensions
of degree equal to the characteristic p. introduced Artin–Schreier theory for extensions of prime degree p, and generalized it to extensions of prime power degree pn.
If K is a field
of characteristic p, a prime number
, any polynomial
of the form
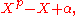
for
in K, is called an Artin–Schreier polynomial. When 
does not lie in the subset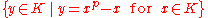 
, this polynomial is irreducible in K[X], and its splitting field
over K is a cyclic extension of K of degree p. This follows since for any root β, the numbers β + i, for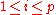
, form all the roots—by Fermat's little theorem
—so the splitting field is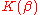
.
Conversely, any Galois extension of K of degree p equal to the characteristic of K is the splitting field of an Artin–Schreier polynomial. This can be proved using additive counterparts of the methods involved in Kummer theory
, such as Hilbert's theorem 90
and additive Galois cohomology
. These extensions are called Artin–Schreier extensions.
Artin–Schreier extensions, play a role in the theory of solvability by radicals, in characteristic p, representing one of the possible classes of extensions in a solvable chain.
They also play a part in the theory of abelian varieties and their isogenies
. In characteristic p, an isogeny of degree p of abelian varieties must, for their function fields, give either an Artin–Schreier extension or a purely inseparable extension.
Witt vector
s, developed by .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Artin–Schreier theory is a branch of Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
, and more specifically is a positive characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
analogue of Kummer theory
Kummer theory
In abstract algebra and number theory, Kummer theory provides a description of certain types of field extensions involving the adjunction of nth roots of elements of the base field. The theory was originally developed by Ernst Eduard Kummer around the 1840s in his pioneering work on Fermat's last...
, for Galois extensions
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of degree equal to the characteristic p. introduced Artin–Schreier theory for extensions of prime degree p, and generalized it to extensions of prime power degree pn.
If K is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of characteristic p, a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, any polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
of the form
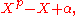
for
in K, is called an Artin–Schreier polynomial. When does not lie in the subset 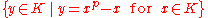, this polynomial is irreducible in K[X], and its splitting fieldSplitting field
In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
over K is a cyclic extension of K of degree p. This follows since for any root β, the numbers β + i, for
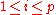, form all the roots—by Fermat's little theoremFermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
—so the splitting field is
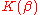.Conversely, any Galois extension of K of degree p equal to the characteristic of K is the splitting field of an Artin–Schreier polynomial. This can be proved using additive counterparts of the methods involved in Kummer theory
Kummer theory
In abstract algebra and number theory, Kummer theory provides a description of certain types of field extensions involving the adjunction of nth roots of elements of the base field. The theory was originally developed by Ernst Eduard Kummer around the 1840s in his pioneering work on Fermat's last...
, such as Hilbert's theorem 90
Hilbert's Theorem 90
In abstract algebra, Hilbert's Theorem 90 refers to an important result on cyclic extensions of fields that leads to Kummer theory...
and additive Galois cohomology
Galois cohomology
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
. These extensions are called Artin–Schreier extensions.
Artin–Schreier extensions, play a role in the theory of solvability by radicals, in characteristic p, representing one of the possible classes of extensions in a solvable chain.
They also play a part in the theory of abelian varieties and their isogenies
Isogeny
In mathematics, an isogeny is a morphism of varieties between two abelian varieties that is surjective and has a finite kernel....
. In characteristic p, an isogeny of degree p of abelian varieties must, for their function fields, give either an Artin–Schreier extension or a purely inseparable extension.
Artin–Schreier–Witt extensions
There is an analogue of Artin–Schreier theory which describes cyclic extensions in characteristic p of p-power degree (not just degree p itself), usingWitt vector
Witt vector
In mathematics, a Witt vector is an infinite sequence of elements of a commutative ring. Ernst Witt showed how to put a ring structure on the set of Witt vectors, in such a way that the ring of Witt vectors over the finite field of order p is the ring of p-adic integers.-Motivation:Any p-adic...
s, developed by .