Unibranch local ring
Encyclopedia
In mathematics
, specifically in algebraic geometry
, a local ring
A is said to be unibranch if the reduced ring
Ared (obtained by quotienting A by its nilradical) is an integral domain, and the integral closure B of Ared is also a local ring. A unibranch local ring is said to be geometrically unibranch if the residue field
of B is a purely inseparable extension of the residue field of Ared.
For definitions, see glossary of scheme theory
. The following result is Corollary IV.4.3.7 of (Grothendieck 1960). See also Zariski's main theorem
.
Theorem. Let X and Y be two integral locally Noetherian schemes and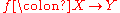
a proper dominant morphism. Denote their function fields by K(X) and K(Y), respectively. Suppose that the algebraic closure of K(Y) in K(X) has separable degree n and that 
is unibranch. Then the fiber 
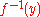has at most n connected components. In particular, if f is birational, then the fibers of unibranch points are connected.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
A is said to be unibranch if the reduced ring
Reduced ring
In ring theory, a ring R is called a reduced ring if it has no non-zero nilpotent elements. Equivalently, a ring is reduced if it has no non-zero elements with square zero, that is, x2 = 0 implies x = 0...
Ared (obtained by quotienting A by its nilradical) is an integral domain, and the integral closure B of Ared is also a local ring. A unibranch local ring is said to be geometrically unibranch if the residue field
Residue field
In mathematics, the residue field is a basic construction in commutative algebra. If R is a commutative ring and m is a maximal ideal, then the residue field is the quotient ring k = R/m, which is a field...
of B is a purely inseparable extension of the residue field of Ared.
Applications
The notions of unibranch and geometrically unibranch points are used in many theorems in algebraic geometry. This section contains one such example.For definitions, see glossary of scheme theory
Glossary of scheme theory
This is a glossary of scheme theory. For an introduction to the theory of schemes in algebraic geometry, see affine scheme, projective space, sheaf and scheme. The concern here is to list the fundamental technical definitions and properties of scheme theory...
. The following result is Corollary IV.4.3.7 of (Grothendieck 1960). See also Zariski's main theorem
Zariski's main theorem
In algebraic geometry, a field in mathematics, Zariski's main theorem is a theorem proved by that states that there is only one branch at any point of a normal variety...
.
Theorem. Let X and Y be two integral locally Noetherian schemes and
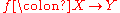a proper dominant morphism. Denote their function fields by K(X) and K(Y), respectively. Suppose that the algebraic closure of K(Y) in K(X) has separable degree n and that is unibranch. Then the fiber 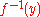has at most n connected components. In particular, if f is birational, then the fibers of unibranch points are connected.