
Adjoint endomorphism
Encyclopedia
In mathematics
, the adjoint endomorphism or adjoint action is an endomorphism
of Lie algebra
s that plays a fundamental role in the development of the theory of Lie algebras and Lie groups.
Given an element x of a Lie algebra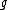 , one defines the adjoint action of x on
, one defines the adjoint action of x on 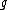 as the endomorphism
as the endomorphism 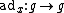 with
with
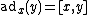
for all y in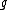 .
.
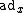 is an action
is an action
that is linear
.
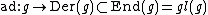 given by
given by 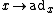 is a representation of a Lie algebra
is a representation of a Lie algebra
and is called the adjoint representation of the algebra. (Here,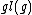 is the Lie algebra of the general linear group
is the Lie algebra of the general linear group
over the vector space . It is isomorphic to
. It is isomorphic to  .)
.)
Within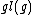 , the composition of two maps is well defined, and the Lie bracket
, the composition of two maps is well defined, and the Lie bracket
may be shown to be given by the commutator of the two elements,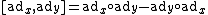
where denotes composition of linear maps. If a basis is chosen for
denotes composition of linear maps. If a basis is chosen for 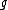 , this corresponds to matrix multiplication
, this corresponds to matrix multiplication
.
Using this and the definition of the Lie bracket in terms of the mapping ad above, the Jacobi identity
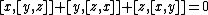
takes the form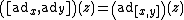
where x, y, and z are arbitrary elements of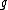 .
.
This last identity confirms that ad really is a Lie algebra homomorphism, in that the morphism ad commutes with the multiplication operator [,].
The kernel of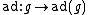 is, by definition, the center of
is, by definition, the center of  .
.
on a Lie algebra is a linear map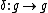 that obeys the Leibniz' law, that is,
that obeys the Leibniz' law, that is,
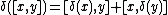
for all x and y in the algebra.
That adx is a derivation is a consequence of the Jacobi identity. This implies that the image of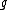 under ad is a subalgebra of
under ad is a subalgebra of 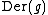 , the space of all derivations of
, the space of all derivations of 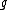 .
.
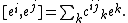
Then the matrix elements for
adei
are given by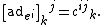
Thus, for example, the adjoint representation of su(2) is the defining rep of so(3).
; crudely, Ad = exp ad, where Ad is the adjoint representation
for a Lie group
.
To be precise, let G be a Lie group, and let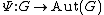 be the mapping
be the mapping 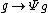 with
with 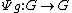 given by the inner automorphism
given by the inner automorphism
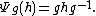
This is called the Lie group map. Define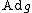 to be the derivative
to be the derivative
of at the origin:
at the origin: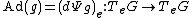
where d is the differential and TeG is the tangent space
at the origin e (e is the identity element of the group G).
The Lie algebra g of G is g=TeG. Since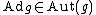 ,
, 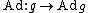 is a map from G to Aut(TeG) which will have a derivative from TeG to End(TeG) (the Lie algebra of Aut(V) is End(V)).
is a map from G to Aut(TeG) which will have a derivative from TeG to End(TeG) (the Lie algebra of Aut(V) is End(V)).
Then we have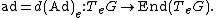
The use of upper-case/lower-case notation is used extensively in the literature. Thus, for example, a vector x in the algebra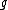 generates a vector field
generates a vector field
X in the group G. Similarly, the adjoint map adxy=[x,y] of vectors in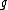 is homomorphic to the Lie derivative
is homomorphic to the Lie derivative
LXY =[X,Y] of vector fields on the group G considered as a manifold
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the adjoint endomorphism or adjoint action is an endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
of Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s that plays a fundamental role in the development of the theory of Lie algebras and Lie groups.
Given an element x of a Lie algebra
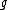 , one defines the adjoint action of x on
, one defines the adjoint action of x on 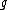 as the endomorphism
as the endomorphism 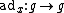 with
with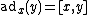
for all y in
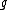 .
.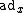 is an action
is an actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
that is linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
.
Adjoint representation
The mapping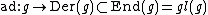 given by
given by 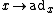 is a representation of a Lie algebra
is a representation of a Lie algebraRepresentation of a Lie algebra
In the mathematical field of representation theory, a Lie algebra representation or representation of a Lie algebra is a way of writing a Lie algebra as a set of matrices in such a way that the Lie bracket is given by the commutator.The notion is closely related to that of a representation of a...
and is called the adjoint representation of the algebra. (Here,
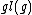 is the Lie algebra of the general linear group
is the Lie algebra of the general linear groupGeneral linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
over the vector space
 . It is isomorphic to
. It is isomorphic to  .)
.)Within
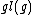 , the composition of two maps is well defined, and the Lie bracket
, the composition of two maps is well defined, and the Lie bracketLie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
may be shown to be given by the commutator of the two elements,
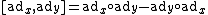
where
 denotes composition of linear maps. If a basis is chosen for
denotes composition of linear maps. If a basis is chosen for 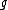 , this corresponds to matrix multiplication
, this corresponds to matrix multiplicationMatrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
.
Using this and the definition of the Lie bracket in terms of the mapping ad above, the Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
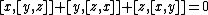
takes the form
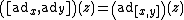
where x, y, and z are arbitrary elements of
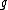 .
.This last identity confirms that ad really is a Lie algebra homomorphism, in that the morphism ad commutes with the multiplication operator [,].
The kernel of
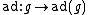 is, by definition, the center of
is, by definition, the center of  .
.Derivation
A derivationDerivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
on a Lie algebra is a linear map
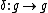 that obeys the Leibniz' law, that is,
that obeys the Leibniz' law, that is,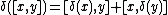
for all x and y in the algebra.
That adx is a derivation is a consequence of the Jacobi identity. This implies that the image of
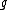 under ad is a subalgebra of
under ad is a subalgebra of 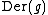 , the space of all derivations of
, the space of all derivations of 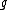 .
.Structure constants
The explicit matrix elements of the adjoint representation are given by the structure constants of the algebra. That is, let {ei} be a set of basis vectors for the algebra, with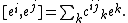
Then the matrix elements for
adei
are given by
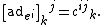
Thus, for example, the adjoint representation of su(2) is the defining rep of so(3).
Relation to Ad
Ad and ad are related through the exponential mapExponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
; crudely, Ad = exp ad, where Ad is the adjoint representation
Adjoint representation
In mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
for a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
.
To be precise, let G be a Lie group, and let
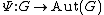 be the mapping
be the mapping 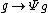 with
with 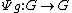 given by the inner automorphism
given by the inner automorphismInner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
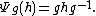
This is called the Lie group map. Define
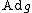 to be the derivative
to be the derivativeTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
of
 at the origin:
at the origin: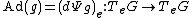
where d is the differential and TeG is the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at the origin e (e is the identity element of the group G).
The Lie algebra g of G is g=TeG. Since
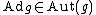 ,
, 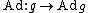 is a map from G to Aut(TeG) which will have a derivative from TeG to End(TeG) (the Lie algebra of Aut(V) is End(V)).
is a map from G to Aut(TeG) which will have a derivative from TeG to End(TeG) (the Lie algebra of Aut(V) is End(V)).Then we have
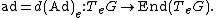
The use of upper-case/lower-case notation is used extensively in the literature. Thus, for example, a vector x in the algebra
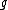 generates a vector field
generates a vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
X in the group G. Similarly, the adjoint map adxy=[x,y] of vectors in
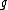 is homomorphic to the Lie derivative
is homomorphic to the Lie derivativeLie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
LXY =[X,Y] of vector fields on the group G considered as a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
.

