
Active contour
Encyclopedia
Active contour model, also called snakes, is a framework for delineating an object outline from a possibly noisy
2D image
.
This framework attempts to minimize an energy
associated to the current contour as a sum of an internal and external energy:
The snakes model is popular in computer vision
, and led to several developments in 2D and 3D. In two dimensions, the active shape model
represents a discrete version of this approach, taking advantage of the point distribution model
to restrict the shape range to an explicit domain learned from a training set.
influenced by constraint and image forces that pull it towards object contours. Snakes are greatly used in applications like object tracking, shape recognition, segmentation, edge detection, stereo matching. Snakes may be understood as a special case of general technique of matching a deformable model to an image by means of energy minimization.
Snake is an “active” model as it always minimizes its energy functional and therefore exhibits dynamic behavior.
A simple elastic snake is thus defined by
One may visualize the snake as a rubber band of arbitrary shape that is deforming with time trying to get as close as possible to the object contour. Snakes do not solve the entire problem of finding contours in images, but rather, they depend on other mechanisms like interaction with a user, interaction with some higher level image understanding process, or information from image data adjacent in time or space. In general, Snake is placed near the object contour. It will dynamically move towards object contour by minimizing its energy iteratively.
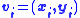
where
We can write its energy function as

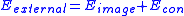
where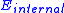 represents the internal energy of the spline (snake) due to bending,
represents the internal energy of the spline (snake) due to bending, 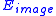 denotes the image forces acting on spline and
denotes the image forces acting on spline and 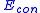 serves as external constraint forces introduced by user. The combination of
serves as external constraint forces introduced by user. The combination of  and
and  can be represented as
can be represented as 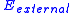 , that denote the external energy acting on the spline.
, that denote the external energy acting on the spline.
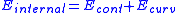
where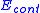 denotes the energy of the snake contour and
denotes the energy of the snake contour and 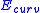 denotes the energy of the spline curvature.
denotes the energy of the spline curvature.


The first-order term makes the snake act like a membrane and second-order term makes it act like a thin plate. Large values of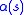 will increase the internal energy of the snake as it stretches more and more, where as small values of
will increase the internal energy of the snake as it stretches more and more, where as small values of  will make the energy function insensitive to the amount of stretch. Similarly, large values of
will make the energy function insensitive to the amount of stretch. Similarly, large values of  will increase the internal energy of the snake as it develops more curves, whereas small values of
will increase the internal energy of the snake as it develops more curves, whereas small values of 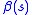 will make the energy function insensitive to curves in the snake. Smaller values of both
will make the energy function insensitive to curves in the snake. Smaller values of both 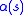 and
and 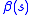 will place fewer constraints on the size and shape of the snake.
will place fewer constraints on the size and shape of the snake.
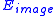 has three components:
has three components:
The energies can be represented as follows:
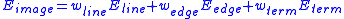
Adjusting the weights in the image will determine salient features in the image which will be considered by the snake.

Depending on the sign of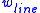 , the line will be attracted to either dark lines or light lines.
, the line will be attracted to either dark lines or light lines.
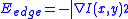
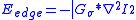
Where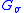 is a Gaussian standard deviation
is a Gaussian standard deviation  minima of this functional lie on zero-crossings
minima of this functional lie on zero-crossings
of
 which define edges in Marr-Hildreth
which define edges in Marr-Hildreth
Theory. Thus the snake gets attracted towards zero-crossing constrained by its own smoothness.
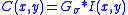 be a slightly smoothed version of the image.Let
be a slightly smoothed version of the image.Let  be the gradient angle.
be the gradient angle.
And let
 be unit vectors along and perpendicular to the gradient direction. The termination functional of energy can be represented as
be unit vectors along and perpendicular to the gradient direction. The termination functional of energy can be represented as
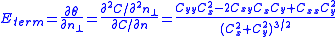
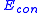 can be used to interactively guide the snakes towards or away from particular features.
can be used to interactively guide the snakes towards or away from particular features.
 and
and
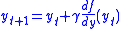
Where controls the size of the step at each iteration.
controls the size of the step at each iteration.
Vector representation: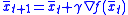
We can approximate the energy function of the snake by using the discrete points on the snake.
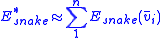
The derivative of above sum is nothing but the sum of derivatives.

Now we should iteratively adjust the points vector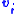 by using gradient descent minimization.
by using gradient descent minimization.

Applying the derivative to energy function gives
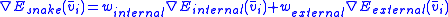
Derivative of internal Energy of the image can be solved as
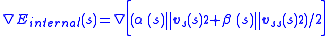
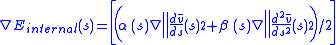
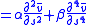
These can be approximated using finite difference
s—the second derivative w.r.t. s can be calculated using three
adjacent points on the snake, and the fourth derivative w.r.t. s can be calculated using five adjacent points. It also helps
to separate the x and y components.
Final equations are

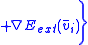

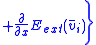

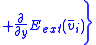
Where

The key drawbacks of the traditional snakes are
Image noise
Image noise is random variation of brightness or color information in images, and is usually an aspect of electronic noise. It can be produced by the sensor and circuitry of a scanner or digital camera...
2D image
Image
An image is an artifact, for example a two-dimensional picture, that has a similar appearance to some subject—usually a physical object or a person.-Characteristics:...
.
This framework attempts to minimize an energy
Graph cuts in computer vision
As applied in the field of computer vision, graph cuts can be employed to efficiently solve a wide variety of low-level computer vision problems , such as image smoothing, the stereo correspondence problem, and many other computer vision problems that can be formulated in terms of energy minimization...
associated to the current contour as a sum of an internal and external energy:
- The external energy is supposed to be minimal when the snake is at the object boundary position. The most straightforward approach consists in giving low values when the regularized gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
around the contour position reaches its peak value. - The internal energy is supposed to be minimal when the snake has a shape which is supposed to be relevant considering the shapeShapeThe shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
of the sought object. The most straightforward approach grants high energy to elongated contours (elastic force) and to bended/high curvatureCurvatureIn mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
contours (rigid force), considering the shape should be as regular and smooth as possible.
The snakes model is popular in computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, and led to several developments in 2D and 3D. In two dimensions, the active shape model
Active shape model
Active shape models are statistical models of the shape of objects which iteratively deform to fit to an example of the object in a new image, developed by Tim Cootes and Chris Taylor in 1995...
represents a discrete version of this approach, taking advantage of the point distribution model
Point distribution model
The point distribution model is a model for representing the mean geometry of a shape and some statistical modes of geometric variation inferred from a training set of shapes.-Background:...
to restrict the shape range to an explicit domain learned from a training set.
Introduction
Snake is an energy minimizing, deformable splineSpline (mathematics)
In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher...
influenced by constraint and image forces that pull it towards object contours. Snakes are greatly used in applications like object tracking, shape recognition, segmentation, edge detection, stereo matching. Snakes may be understood as a special case of general technique of matching a deformable model to an image by means of energy minimization.
Snake is an “active” model as it always minimizes its energy functional and therefore exhibits dynamic behavior.
A simple elastic snake is thus defined by
- a set of n points
- an internal elastic energy term
- an external edge based energy term
One may visualize the snake as a rubber band of arbitrary shape that is deforming with time trying to get as close as possible to the object contour. Snakes do not solve the entire problem of finding contours in images, but rather, they depend on other mechanisms like interaction with a user, interaction with some higher level image understanding process, or information from image data adjacent in time or space. In general, Snake is placed near the object contour. It will dynamically move towards object contour by minimizing its energy iteratively.
Energy function
In Snakes, we use the technique of matching a deformable model to an image by means of energy minimization. A snake initialized near the target gets refined iteratively and is attracted towards the salient contour. A snake in the image can be represented as a set of n points.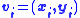
where

We can write its energy function as

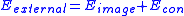
where
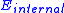 represents the internal energy of the spline (snake) due to bending,
represents the internal energy of the spline (snake) due to bending, 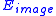 denotes the image forces acting on spline and
denotes the image forces acting on spline and 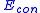 serves as external constraint forces introduced by user. The combination of
serves as external constraint forces introduced by user. The combination of  and
and  can be represented as
can be represented as 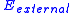 , that denote the external energy acting on the spline.
, that denote the external energy acting on the spline.Internal energy
Internal Energy of the snake is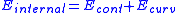
where
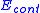 denotes the energy of the snake contour and
denotes the energy of the snake contour and 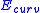 denotes the energy of the spline curvature.
denotes the energy of the spline curvature.

The first-order term makes the snake act like a membrane and second-order term makes it act like a thin plate. Large values of
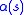 will increase the internal energy of the snake as it stretches more and more, where as small values of
will increase the internal energy of the snake as it stretches more and more, where as small values of  will make the energy function insensitive to the amount of stretch. Similarly, large values of
will make the energy function insensitive to the amount of stretch. Similarly, large values of  will increase the internal energy of the snake as it develops more curves, whereas small values of
will increase the internal energy of the snake as it develops more curves, whereas small values of 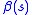 will make the energy function insensitive to curves in the snake. Smaller values of both
will make the energy function insensitive to curves in the snake. Smaller values of both 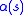 and
and 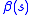 will place fewer constraints on the size and shape of the snake.
will place fewer constraints on the size and shape of the snake.Image forces
Further,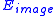 has three components:
has three components:
- Lines
- Edges
- Terminations
The energies can be represented as follows:
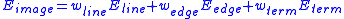
Adjusting the weights in the image will determine salient features in the image which will be considered by the snake.
Line functional
A line functional is nothing but the intensity of the image, which can be represented as
Depending on the sign of
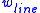 , the line will be attracted to either dark lines or light lines.
, the line will be attracted to either dark lines or light lines.Edge functional
Edges in the image can be found by the following energy function which will make the snake attract towards contours with large image gradients.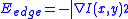
Scale space
It is rather common that a snake started far from the object converges to the desired object contour. If a part of the snake finds a low energy feature, it pulls the other parts of the snake to continue to the contour. Scale Space continuation can be used in order to achieve desired results. One can allow the snake to come to equilibrium on a blurry energy edge functional and reduce the blurring as the calculation progresses. The energy functional is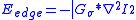
Where
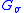 is a Gaussian standard deviation
is a Gaussian standard deviation  minima of this functional lie on zero-crossings
minima of this functional lie on zero-crossingsZero crossing
Zero-crossing is a commonly used term in electronics, mathematics, and image processing. In mathematical terms, a "zero-crossing" is a point where the sign of a function changes Zero-crossing is a commonly used term in electronics, mathematics, and image processing. In mathematical terms, a...
of
 which define edges in Marr-Hildreth
which define edges in Marr-HildrethMarr-Hildreth algorithm
In computer vision, the Marr–Hildreth algorithm is a method of detecting edges in digital images, that is continuous curves where there are strong and rapid variations in image brightness. The Marr–Hildreth edge detection method is simple and operates by convolving the image with the Laplacian of...
Theory. Thus the snake gets attracted towards zero-crossing constrained by its own smoothness.
Termination functional
Curvature of level lines in a slightly smoothed image is used to detect corners and terminations in an image. Let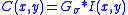 be a slightly smoothed version of the image.Let
be a slightly smoothed version of the image.Let  be the gradient angle.
be the gradient angle.And let
 be unit vectors along and perpendicular to the gradient direction. The termination functional of energy can be represented as
be unit vectors along and perpendicular to the gradient direction. The termination functional of energy can be represented as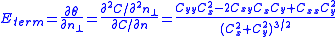
Constraint energy
Some systems, including the original snakes implementation, allowed for user interaction to guide the snakes, not only in initial placement but also in their energy terms. Such constraint energy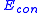 can be used to interactively guide the snakes towards or away from particular features.
can be used to interactively guide the snakes towards or away from particular features.Implementation
Gradient-descent minimization is one of the simple optimization which can be used to minimize snake energy. For example, let’s consider a function of only one variable. If we have a starting guess at the value of the solution,we can look at the slope at that point and decide to increment our solution (negative slope) or decrement our solution (positive slope). Notice the negation there: if the slope is positive, downhill is backwards; and if the slope is negative, downhill is forwards. We can thus implement gradient-descent minimization as and
and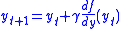
Where
 controls the size of the step at each iteration.
controls the size of the step at each iteration.Vector representation:
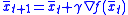
We can approximate the energy function of the snake by using the discrete points on the snake.
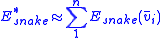
The derivative of above sum is nothing but the sum of derivatives.

Now we should iteratively adjust the points vector
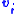 by using gradient descent minimization.
by using gradient descent minimization.
Applying the derivative to energy function gives
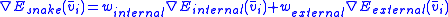
Derivative of internal Energy of the image can be solved as
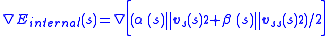
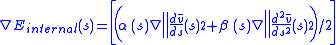
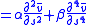
These can be approximated using finite difference
Finite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
s—the second derivative w.r.t. s can be calculated using three
adjacent points on the snake, and the fourth derivative w.r.t. s can be calculated using five adjacent points. It also helps
to separate the x and y components.
Final equations are

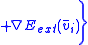

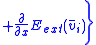

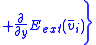
Where

Pseudo code
- Before entering the iteration calculate
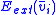 and the derivatives of this w.r.t. x and y separately.
and the derivatives of this w.r.t. x and y separately. - At the start of the iteration, calculate
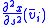 and
and  using the three adjacent points and
using the three adjacent points and  using five adjacent points.
using five adjacent points. - Then, calculate change in x and y for each point in
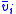 Use the precalculated
Use the precalculated 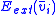 .
.
Advantages and drawbacks
Snakes have multiple advantages over classical feature attraction techniques.- Snakes are autonomous and self-adapting in their search for a minimal energy state.
- They can be easily manipulated using external image forces.
- They can be made sensitive to image scale by incorporating Gaussian smoothing in the image energy function.
- They can be used to track dynamic objects in temporal as well as the spatial dimensions.
The key drawbacks of the traditional snakes are
- They can often get stuck in local minima states; this may be overcome by using simulated annealing techniques at the expense of longer computation times.
- They often overlook minute features in the process of minimizing the energy over the entire path of their contours.
- Their accuracy is governed by the convergence criteria used in the energy minimization technique; higher accuracies require tighter convergence criteria and hence, longer computation times.
GVF active contours
The snake is developed based on new type of external field,called Gradient Vector Flow, or GVF. This computation causes diffuse forces to exist far from the object, and crisp force vectors near the edges. Combining these forces with the usual internal forces yields a powerful computational object: the GVF snake (2D), or the GVF deformable model (N-D). Even though this snake is started far from the object, it still gets attracted towards the object. Especially, GVF active contours can handle broken object edges and subjective contours.Balloon snake
In this case,snake behaves like a balloon which is blown up. When it passes by edges, it is stopped if the contour is strong,or passes through if the contour is too weak. Thus, the initial snake need not be too close to the solution(object) to converge. This approach modifies the definition external forces (derived from gradient of the image) presented in traditional snake (Kass et al). A new pressure force is introduced which makes the curve behave like a balloon.Diffusion snakes
The diffusion snake is a modification of the Mumford-Shah functional for spline contours. A modification of the Mumford-Shah functional and its cartoon limit is used to incorporate statistical prior on the shape of the segmenting contour.By minimizing a single energy functional, we obtain a segmentation process which maximizes both the Grey value homogeneity in the separated regions and the similarity of the contour with respect to a set of training shapes.Sample code
- Practical examples of different snakes developed by Prince and Xu
- Basic tool to play with snakes (active contour models) from Tim Cootes,University of Manchester
- Matlab implementation of 2D and 3D snake including GVF and balloon force
- Matlab Snake Demo by Chris Bregler and Malcom Slaney,Interval Research Corporation.
- A Demonstration Using Java
- Chan-Vese algorithm (Active Contours), including implementation in MATLAB

