Point distribution model
Encyclopedia
The point distribution model is a model for representing the mean geometry of a shape and some statistical modes of geometric variation inferred from a training set of shapes.
for the statistical study of shape
and for segmentation of medical images
where shape priors really help interpretation of noisy and low-contrasted pixel
s/voxel
s. The latter point leads to active shape model
s (ASM) and active appearance model
s (AAM).
Point distribution models rely on landmark point
s. A landmark is an annotating point posed by an anatomist onto a given locus for every shape instance across the training set population. For instance, the same landmark will designate the tip of the index finger
in a training set of 2D hands outlines. Principal component analysis (PCA), for instance, is a relevant tool for studying correlations of movement between groups of landmarks among the training set population. Typically, it might detect that all the landmarks located along the same finger move exactly together across the training set examples showing different finger spacing for a flat-posed hands collection.
, which minimizes the least squared error between the points.
aligned landmarks in two dimensions are given as
.
It's important to note that each landmark
should represent the same anatomical location. For example, landmark #3,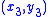 
might represent the tip of the ring finger across all training images.
Now the shape outlines are reduced to sequences of
landmarks, so that a given training shape is defined as the vector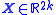 
. Assuming the scattering is gaussian in this space, PCA is used to compute normalized eigenvectors and eigenvalues of the covariance matrix
across all training shapes. The matrix of the top
eigenvectors is given as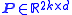 
, and each eigenvector describes a principal mode of variation along the set.
Finally, a linear combination
of the eigenvectors is used to define a new shape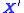
, mathematically defined as:
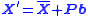
where
is defined as the mean shape across all training images, and 
is a vector of scaling values for each principal component. Therefore, by modifying the variable 
an infinite number of shapes can be defined. To ensure that the new shapes are all within the variation seen in the training set, it is common to only allow each element of 
to be within 
3 standard deviations, where the standard deviation of a given principal component is defined as the square root of its corresponding eigenvalue.
PDM's can be extended to any arbitrary number of dimensions, but are typically used in 2D image and 3D volume applications (where each landmark point is
or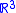 
).
, can be seen as a sequence of
euclidean vectors associated to corresponding landmark and designating a compound move for the whole shape. Global nonlinear variation is usually well handled provided nonlinear variation is kept to a reasonable level. Typically, a twisting nematode worm is used as an example in the teaching of kernel PCA-based methods.
Due to the PCA properties: eigenvectors are mutually orthogonal, form a basis of the training set cloud in the shape space, and cross at the 0 in this space, which represents the mean shape. Also, PCA is a traditional way of fitting a closed ellipsoid to a Gaussian cloud of points (whatever their dimension): this suggests the concept of bounded variation.
The idea behind PDM's is that eigenvectors can be linearly combined to create an infinity of new shape instances that will 'look like' the one in the training set. The coefficients are bounded alike the values of the corresponding eigenvalues, so as to ensure the generated 2n/3n-dimensional dot will remain into the hyper-ellipsoidal allowed domain—allowable shape domain (ASD).
Background
It has been developed by Cootes, Taylor et al. and became a standard in computer visionComputer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
for the statistical study of shape
Statistical shape analysis
Statistical shape analysis is a geometrical analysis from a set of shapes in which statistics are measured to describe geometrical properties from similar shapes or different groups, for instance, the difference between male and female Gorilla skull shapes, normal and pathological bone shapes, etc...
and for segmentation of medical images
Medical imaging
Medical imaging is the technique and process used to create images of the human body for clinical purposes or medical science...
where shape priors really help interpretation of noisy and low-contrasted pixel
Pixel
In digital imaging, a pixel, or pel, is a single point in a raster image, or the smallest addressable screen element in a display device; it is the smallest unit of picture that can be represented or controlled....
s/voxel
Voxel
A voxel is a volume element, representing a value on a regular grid in three dimensional space. This is analogous to a pixel, which represents 2D image data in a bitmap...
s. The latter point leads to active shape model
Active shape model
Active shape models are statistical models of the shape of objects which iteratively deform to fit to an example of the object in a new image, developed by Tim Cootes and Chris Taylor in 1995...
s (ASM) and active appearance model
Active Appearance Model
An active appearance model is a computer vision algorithm for matching a statistical model of object shape and appearance to a new image. They are built during a training phase...
s (AAM).
Point distribution models rely on landmark point
Landmark point
In morphometrics, landmark point or shortly landmark is a point in a shape object in which correspondences between and within the populations of the object are preserved. In other disciplines, landmarks may be known as vertices, anchor points, control points, sites, profile points, 'sampling'...
s. A landmark is an annotating point posed by an anatomist onto a given locus for every shape instance across the training set population. For instance, the same landmark will designate the tip of the index finger
Index finger
The index finger, , is the first finger and the second digit of a human hand. It is located between the first and third digits, between the thumb and the middle finger...
in a training set of 2D hands outlines. Principal component analysis (PCA), for instance, is a relevant tool for studying correlations of movement between groups of landmarks among the training set population. Typically, it might detect that all the landmarks located along the same finger move exactly together across the training set examples showing different finger spacing for a flat-posed hands collection.
Details
First, a set of training images are manually landmarked with enough corresponding landmarks to sufficiently approximate the geometry of the original shapes. These landmarks are aligned using the generalized procrustes analysisGeneralized Procrustes analysis
Generalized Procrustes analysis is a method of statistical analysis that can be used to compare the shapes of objects, or the results of surveys, interviews, panels. It was developed for analyising the results of free-choice profiling, a survey technique which allows respondents to describe a...
, which minimizes the least squared error between the points.
aligned landmarks in two dimensions are given as.It's important to note that each landmark
should represent the same anatomical location. For example, landmark #3, 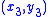might represent the tip of the ring finger across all training images.Now the shape outlines are reduced to sequences of
landmarks, so that a given training shape is defined as the vector 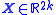. Assuming the scattering is gaussian in this space, PCA is used to compute normalized eigenvectors and eigenvalues of the covariance matrixCovariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
across all training shapes. The matrix of the top
eigenvectors is given as 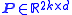, and each eigenvector describes a principal mode of variation along the set.Finally, a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the eigenvectors is used to define a new shape
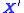, mathematically defined as: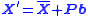where
is defined as the mean shape across all training images, and is a vector of scaling values for each principal component. Therefore, by modifying the variable an infinite number of shapes can be defined. To ensure that the new shapes are all within the variation seen in the training set, it is common to only allow each element of to be within 3 standard deviations, where the standard deviation of a given principal component is defined as the square root of its corresponding eigenvalue.PDM's can be extended to any arbitrary number of dimensions, but are typically used in 2D image and 3D volume applications (where each landmark point is
or 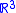).Discussion
An eigenvector, interpreted in euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, can be seen as a sequence of
euclidean vectors associated to corresponding landmark and designating a compound move for the whole shape. Global nonlinear variation is usually well handled provided nonlinear variation is kept to a reasonable level. Typically, a twisting nematode worm is used as an example in the teaching of kernel PCA-based methods.Due to the PCA properties: eigenvectors are mutually orthogonal, form a basis of the training set cloud in the shape space, and cross at the 0 in this space, which represents the mean shape. Also, PCA is a traditional way of fitting a closed ellipsoid to a Gaussian cloud of points (whatever their dimension): this suggests the concept of bounded variation.
The idea behind PDM's is that eigenvectors can be linearly combined to create an infinity of new shape instances that will 'look like' the one in the training set. The coefficients are bounded alike the values of the corresponding eigenvalues, so as to ensure the generated 2n/3n-dimensional dot will remain into the hyper-ellipsoidal allowed domain—allowable shape domain (ASD).
External links
- Flexible Models for Computer Vision, Tim Cootes, Manchester University.
- A practical introduction to PDM and ASMs.