
Abelian integral
Encyclopedia
In mathematics
, an abelian integral, named after the Norwegian mathematician Niels Abel
, is an integral in the complex plane
of the form
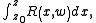
where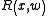 is an arbitrary rational function
is an arbitrary rational function
of the two variables and
and 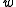 . These variables are related by the equation
. These variables are related by the equation
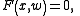
where is an irreducible polynomial in
is an irreducible polynomial in 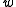 ,
,
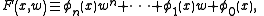
whose coefficients ,
,  are rational function
are rational function
s of . The value of an abelian integral depends not only on the integration limits but also on the path along which the integral is taken, and it is thus a multivalued function
. The value of an abelian integral depends not only on the integration limits but also on the path along which the integral is taken, and it is thus a multivalued function
of .
.
Abelian integrals are natural generalizations of elliptic integral
s, which arise when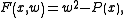
where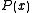 is a polynomial of degree 3 or 4. Another special case of an abelian integral is a hyperelliptic integral, where
is a polynomial of degree 3 or 4. Another special case of an abelian integral is a hyperelliptic integral, where 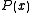 , in the formula above, is a polynomial of degree greater than 4.
, in the formula above, is a polynomial of degree greater than 4.
, or more precisely in the way an algebraic curve
can be mapped into abelian varieties. The Abelian Integral was later connected to the prominent mathematician David Hilbert
's 16th Problem and continues to be considered one of the foremost challenges to contemporary analysis (mathematics).
theory, an abelian integral is a function related to the indefinite integral of a differential of the first kind
. Suppose we are given a Riemann surface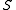 and on it a differential 1-form
and on it a differential 1-form
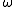 that is everywhere holomorphic on
that is everywhere holomorphic on  , and fix a point
, and fix a point 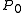 on
on 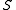 , from which to integrate. We can regard
, from which to integrate. We can regard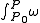
as a multi-valued function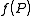 , or (better) an honest function of the chosen path
, or (better) an honest function of the chosen path 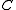 drawn on
drawn on  from
from  to
to 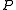 . Since
. Since  will in general be multiply connected, one should specify
will in general be multiply connected, one should specify 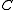 , but the value will in fact only depend on the homology class of
, but the value will in fact only depend on the homology class of  .
.
In the case of a compact Riemann surface
a compact Riemann surface
of genus
1, i.e. an elliptic curve
, such functions are the elliptic integral
s. Logically speaking, therefore, an abelian integral should be a function such as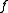 .
.
Such functions were first introduced to study hyperelliptic integrals, i.e. for the case where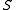 is a hyperelliptic curve. This is a natural step in the theory of integration to the case of integrals involving algebraic function
is a hyperelliptic curve. This is a natural step in the theory of integration to the case of integrals involving algebraic function
s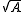 , where
, where 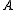 is a polynomial
is a polynomial
of degree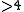 . The first major insights of the theory were given by Niels Abel; it was later formulated in terms of the Jacobian variety
. The first major insights of the theory were given by Niels Abel; it was later formulated in terms of the Jacobian variety
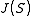 . Choice of
. Choice of 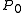 gives rise to a standard holomorphic mapping
gives rise to a standard holomorphic mapping
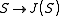
of complex manifold
s. It has the defining property that the holomorphic 1-forms on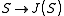 , of which there are g independent ones if g is the genus of S, pull back to a basis for the differentials of the first kind on S.
, of which there are g independent ones if g is the genus of S, pull back to a basis for the differentials of the first kind on S.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an abelian integral, named after the Norwegian mathematician Niels Abel
Niels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
, is an integral in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
of the form
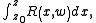
where
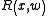 is an arbitrary rational function
is an arbitrary rational functionRational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
of the two variables
 and
and 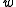 . These variables are related by the equation
. These variables are related by the equation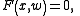
where
 is an irreducible polynomial in
is an irreducible polynomial in 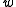 ,
,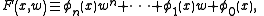
whose coefficients
 ,
,  are rational function
are rational functionRational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s of
 . The value of an abelian integral depends not only on the integration limits but also on the path along which the integral is taken, and it is thus a multivalued function
. The value of an abelian integral depends not only on the integration limits but also on the path along which the integral is taken, and it is thus a multivalued functionMultivalued function
In mathematics, a multivalued function is a left-total relation; i.e. every input is associated with one or more outputs...
of
 .
.Abelian integrals are natural generalizations of elliptic integral
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
s, which arise when
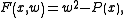
where
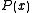 is a polynomial of degree 3 or 4. Another special case of an abelian integral is a hyperelliptic integral, where
is a polynomial of degree 3 or 4. Another special case of an abelian integral is a hyperelliptic integral, where 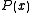 , in the formula above, is a polynomial of degree greater than 4.
, in the formula above, is a polynomial of degree greater than 4.History
The theory of abelian integrals originated with the paper by Abel published in 1841. This paper was written during his stay in Paris in 1826 and presented to Cauchy in October of the same year. This theory, later fully developed by others, was one of the crowning achievements of nineteenth century mathematics and has had a major impact on the development of modern mathematics. In more abstract and geometric language, it is contained in the concept of abelian varietyAbelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
, or more precisely in the way an algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
can be mapped into abelian varieties. The Abelian Integral was later connected to the prominent mathematician David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
's 16th Problem and continues to be considered one of the foremost challenges to contemporary analysis (mathematics).
Modern view
In Riemann surfaceRiemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
theory, an abelian integral is a function related to the indefinite integral of a differential of the first kind
Differential of the first kind
In mathematics, differential of the first kind is a traditional term used in the theories of Riemann surfaces and algebraic curves , for everywhere-regular differential 1-forms...
. Suppose we are given a Riemann surface
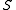 and on it a differential 1-form
and on it a differential 1-formDifferential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
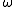 that is everywhere holomorphic on
that is everywhere holomorphic on  , and fix a point
, and fix a point 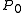 on
on 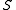 , from which to integrate. We can regard
, from which to integrate. We can regard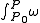
as a multi-valued function
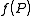 , or (better) an honest function of the chosen path
, or (better) an honest function of the chosen path 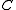 drawn on
drawn on  from
from  to
to 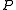 . Since
. Since  will in general be multiply connected, one should specify
will in general be multiply connected, one should specify 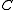 , but the value will in fact only depend on the homology class of
, but the value will in fact only depend on the homology class of  .
.In the case of
 a compact Riemann surface
a compact Riemann surfaceCompact Riemann surface
In mathematics, a compact Riemann surface is a complex manifold of dimension one that is a compact space. Riemann surfaces are generally classified first into the compact and the open .A compact Riemann surface C that is a...
of genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
1, i.e. an elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
, such functions are the elliptic integral
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
s. Logically speaking, therefore, an abelian integral should be a function such as
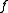 .
.Such functions were first introduced to study hyperelliptic integrals, i.e. for the case where
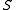 is a hyperelliptic curve. This is a natural step in the theory of integration to the case of integrals involving algebraic function
is a hyperelliptic curve. This is a natural step in the theory of integration to the case of integrals involving algebraic functionAlgebraic function
In mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
s
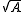 , where
, where 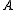 is a polynomial
is a polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
of degree
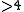 . The first major insights of the theory were given by Niels Abel; it was later formulated in terms of the Jacobian variety
. The first major insights of the theory were given by Niels Abel; it was later formulated in terms of the Jacobian varietyJacobian variety
In mathematics, the Jacobian variety J of a non-singular algebraic curve C of genus g is the moduli space of degree 0 line bundles...
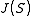 . Choice of
. Choice of 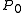 gives rise to a standard holomorphic mapping
gives rise to a standard holomorphic mappingFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
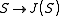
of complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s. It has the defining property that the holomorphic 1-forms on
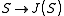 , of which there are g independent ones if g is the genus of S, pull back to a basis for the differentials of the first kind on S.
, of which there are g independent ones if g is the genus of S, pull back to a basis for the differentials of the first kind on S.

