
10-polytope
Encyclopedia
10-simplex 10-simplex In geometry, a 10-simplex is a self-dual regular 10-polytope. It has 11 vertices, 55 edges, 165 triangle faces, 330 tetrahedral cells, 462 5-cell 4-faces, 462 5-simplex 5-faces, 330 6-simplex 6-faces, 165 7-simplex 7-faces, 55 8-simplex 8-faces, and 11 9-simplex 9-faces... |
Truncated 10-simplex |
Rectified 10-simplex Rectified 10-simplex In ten-dimensional geometry, a rectified 10-simplex is a convex uniform 10-polytope, being a rectification of the regular 10-simplex.These polytopes are part of a family of 527 uniform 10-polytopes with A10 symmetry.... |
|||||||||
Cantellated 10-simplex |
Runcinated 10-simplex |
||||||||||
Stericated 10-simplex |
Pentallated 10-simplex |
Hexicated 10-simplex |
|||||||||
Heptellated 10-simplex |
Octellated 10-simplex |
Ennecated 10-simplex |
|||||||||
10-orthoplex |
Truncated 10-orthoplex |
Rectified 10-orthoplex Rectified 10-orthoplex In ten-dimensional geometry, a rectified 10-orthoplex is a convex uniform 10-polytope, being a rectification of the regular 10-orthoplex.There are 10 rectifications of the 10-orthoplex. Vertices of the rectified 10-orthoplex are located at the edge-centers of the 9-orthoplex. Vertices of the... |
|||||||||
10-cube 10-cube In geometry, a 10-cube is a ten-dimensional hypercube. It has 1024 vertices, 5120 edges, 11520 square faces, 15360 cubic cells, 13440 tesseract 4-faces, 8064 5-cube 5-faces, 3360 6-cube 6-faces, 960 7-cube 7-faces, 180 8-cube 8-faces, and 20 9-cube 9-faces.... |
Truncated 10-cube |
Rectified 10-cube Rectified 10-cube In ten-dimensional geometry, a rectified 10-cube is a convex uniform 10-polytope, being a rectification of the regular 10-cube.There are 10 rectifications of the 10-cube, with the zeroth being the 10-cube itself. Vertices of the rectified 10-cube are located at the edge-centers of the 10-cube... |
|||||||||
10-demicube 10-demicube In geometry, a demidekeract or 10-demicube is a uniform 10-polytope, constructed from the 10-cube with alternated vertices deleted. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes.... |
Truncated 10-demicube |
||||||||||
In ten-dimensional geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a 10-polytope is a 10 dimensional polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
contained by 9-polytope facets. Each 8-polytope
8-polytope
In eight-dimensional geometry, a polyzetton is a polytope contained by 7-polytope facets. Each 6-polytope ridge being shared by exactly two 7-polytope facets....
ridge
Ridge (geometry)
In geometry, a ridge is an -dimensional element of an n-dimensional polytope. It is also sometimes called a subfacet for having one lower dimension than a facet.By dimension, this corresponds to:*a vertex of a polygon;...
being shared by exactly two 9-polytope
9-polytope
In nine-dimensional geometry, a polyyotton is a polytope contained by 8-polytope facets. Each 7-polytope ridge being shared by exactly two 8-polytope facets....
facets
Facet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
.
A uniform 10-polytope is one which is vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
, and constructed from uniform facets.
A proposed name for 10-polytope is polyxennon (plural: polyxenna), created from poly- xenna (a variation on ennea
Ennea
Ennea was the second album by jazz-rock fusion band Chase. It did not repeat the commercial success of their debut album, mostly due to the lack of a top 40 hit and the extended suite to Greek Mythology on side 2, which lacked the "commercial appeal" the first LP had...
meaning nine) and -on.
Regular 10-polytopes
Regular 10-polytopes can be represented by the Schläfli symbol {p,q,r,s,t,u,v,w,x}, with x {p,q,r,s,t,u,v,w} 9-polytope facetsFacet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
around each peak
Peak (geometry)
In geometry, a peak is an -face of an n-dimensional polytope. A peak attaches at least three facets ....
.
There are exactly three such convex regular 10-polytopes:
- {3,3,3,3,3,3,3,3,3} - 10-simplex10-simplexIn geometry, a 10-simplex is a self-dual regular 10-polytope. It has 11 vertices, 55 edges, 165 triangle faces, 330 tetrahedral cells, 462 5-cell 4-faces, 462 5-simplex 5-faces, 330 6-simplex 6-faces, 165 7-simplex 7-faces, 55 8-simplex 8-faces, and 11 9-simplex 9-faces...
- {4,3,3,3,3,3,3,3,3} - 10-cube10-cubeIn geometry, a 10-cube is a ten-dimensional hypercube. It has 1024 vertices, 5120 edges, 11520 square faces, 15360 cubic cells, 13440 tesseract 4-faces, 8064 5-cube 5-faces, 3360 6-cube 6-faces, 960 7-cube 7-faces, 180 8-cube 8-faces, and 20 9-cube 9-faces....
- {3,3,3,3,3,3,3,3,4} - 10-orthoplex
There are no nonconvex regular 10-polytopes.
Euler characteristic
The Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
for 10-polytopes that are topological 9-spheres (including all convex 10-polytopes) is zero. χ=V-E+F-C+f4-f5+f6-f7+f8-f9=0.
Uniform 10-polytopes by fundamental Coxeter groups
Uniform 10-polytopes with reflective symmetry can be generated by these three Coxeter groups, represented by permutations of rings of the Coxeter-Dynkin diagramCoxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
s:
| # | Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
|---|---|---|---|
| 1 | A10 | [39] | |
| 2 | B10 | [4,38] | |
| 3 | D10 | [37,1,1] |
Selected regular and uniform 10-polytopes from each family include:
- SimplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
family: A10 [39] -- 527 uniform 10-polytopes as permutations of rings in the group diagram, including one regular:
- {39} - 10-simplex10-simplexIn geometry, a 10-simplex is a self-dual regular 10-polytope. It has 11 vertices, 55 edges, 165 triangle faces, 330 tetrahedral cells, 462 5-cell 4-faces, 462 5-simplex 5-faces, 330 6-simplex 6-faces, 165 7-simplex 7-faces, 55 8-simplex 8-faces, and 11 9-simplex 9-faces...
-
- {39} - 10-simplex
- 527 uniform 10-polytopes as permutations of rings in the group diagram, including one regular:
- HypercubeHypercubeIn geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
/orthoplex family: B10 [4,38] -- 1023 uniform 10-polytopes as permutations of rings in the group diagram, including two regular ones:
- {4,38} - 10-cube10-cubeIn geometry, a 10-cube is a ten-dimensional hypercube. It has 1024 vertices, 5120 edges, 11520 square faces, 15360 cubic cells, 13440 tesseract 4-faces, 8064 5-cube 5-faces, 3360 6-cube 6-faces, 960 7-cube 7-faces, 180 8-cube 8-faces, and 20 9-cube 9-faces....
or dekeract - - {38,4} - 10-orthoplex or decacross -
- h{4,38} - 10-demicube10-demicubeIn geometry, a demidekeract or 10-demicube is a uniform 10-polytope, constructed from the 10-cube with alternated vertices deleted. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes....
.
- {4,38} - 10-cube
- 1023 uniform 10-polytopes as permutations of rings in the group diagram, including two regular ones:
- Demihypercube D10 family: [37,1,1] -
- 767 uniform 10-polytopes as permutations of rings in the group diagram, including:
- 17,1 - 10-demicube10-demicubeIn geometry, a demidekeract or 10-demicube is a uniform 10-polytope, constructed from the 10-cube with alternated vertices deleted. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes....
or demidekeract - - 71,1 - 10-orthoplex -
- 17,1 - 10-demicube
- 767 uniform 10-polytopes as permutations of rings in the group diagram, including:
The A10 family
The A10 family has symmetry of order 39,916,800 (11 factorialFactorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
).
There are 512+16-1=527 forms based on all permutations of the Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
s with one or more rings. 31 are shown below: all one and two ringed forms, and the final omnitruncated form. Bowers-style acronym names are given in parentheses for cross-referencing.
| # | Graph | Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... Schläfli symbol Name |
Element counts | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9-faces | 8-faces | 7-faces | 6-faces | 5-faces | 4-faces | Cells | Faces | Edges | Vertices | |||
| 1 | t0{3,3,3,3,3,3,3,3,3} 10-simplex 10-simplex In geometry, a 10-simplex is a self-dual regular 10-polytope. It has 11 vertices, 55 edges, 165 triangle faces, 330 tetrahedral cells, 462 5-cell 4-faces, 462 5-simplex 5-faces, 330 6-simplex 6-faces, 165 7-simplex 7-faces, 55 8-simplex 8-faces, and 11 9-simplex 9-faces... (ux) |
11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | |
| 2 | t1{3,3,3,3,3,3,3,3,3} Rectified 10-simplex Rectified 10-simplex In ten-dimensional geometry, a rectified 10-simplex is a convex uniform 10-polytope, being a rectification of the regular 10-simplex.These polytopes are part of a family of 527 uniform 10-polytopes with A10 symmetry.... (ru) |
495 | 55 | |||||||||
| 3 | t2{3,3,3,3,3,3,3,3,3} Birectified 10-simplex (bru) |
1980 | 165 | |||||||||
| 4 | t3{3,3,3,3,3,3,3,3,3} Trirectified 10-simplex (tru) |
4620 | 330 | |||||||||
| 5 | t4{3,3,3,3,3,3,3,3,3} Quadrirectified 10-simplex (teru) |
6930 | 462 | |||||||||
| 6 | t0,1{3,3,3,3,3,3,3,3,3} Truncated 10-simplex (tu) |
550 | 110 | |||||||||
| 7 | t0,2{3,3,3,3,3,3,3,3,3} Cantellated 10-simplex |
4455 | 495 | |||||||||
| 8 | t1,2{3,3,3,3,3,3,3,3,3} Bitruncated 10-simplex |
2475 | 495 | |||||||||
| 9 | t0,3{3,3,3,3,3,3,3,3,3} Runcinated 10-simplex |
15840 | 1320 | |||||||||
| 10 | t1,3{3,3,3,3,3,3,3,3,3} Bicantellated 10-simplex |
17820 | 1980 | |||||||||
| 11 | t2,3{3,3,3,3,3,3,3,3,3} Tritruncated 10-simplex |
6600 | 1320 | |||||||||
| 12 | t0,4{3,3,3,3,3,3,3,3,3} Stericated 10-simplex |
32340 | 2310 | |||||||||
| 13 | t1,4{3,3,3,3,3,3,3,3,3} Biruncinated 10-simplex |
55440 | 4620 | |||||||||
| 14 | t2,4{3,3,3,3,3,3,3,3,3} Tricantellated 10-simplex |
41580 | 4620 | |||||||||
| 15 | t3,4{3,3,3,3,3,3,3,3,3} Quadritruncated 10-simplex |
11550 | 2310 | |||||||||
| 16 | t0,5{3,3,3,3,3,3,3,3,3} Pentellated 10-simplex |
41580 | 2772 | |||||||||
| 17 | t1,5{3,3,3,3,3,3,3,3,3} Bistericated 10-simplex |
97020 | 6930 | |||||||||
| 18 | t2,5{3,3,3,3,3,3,3,3,3} Triruncinated 10-simplex |
110880 | 9240 | |||||||||
| 19 | t3,5{3,3,3,3,3,3,3,3,3} Quadricantellated 10-simplex |
62370 | 6930 | |||||||||
| 20 | t4,5{3,3,3,3,3,3,3,3,3} Quintitruncated 10-simplex |
13860 | 2772 | |||||||||
| 21 | t0,6{3,3,3,3,3,3,3,3,3} Hexicated 10-simplex |
34650 | 2310 | |||||||||
| 22 | t1,6{3,3,3,3,3,3,3,3,3} Bipentellated 10-simplex |
103950 | 6930 | |||||||||
| 23 | t2,6{3,3,3,3,3,3,3,3,3} Tristericated 10-simplex |
161700 | 11550 | |||||||||
| 24 | t3,6{3,3,3,3,3,3,3,3,3} Quadriruncinated 10-simplex |
138600 | 11550 | |||||||||
| 25 | t0,7{3,3,3,3,3,3,3,3,3} Heptellated 10-simplex |
18480 | 1320 | |||||||||
| 26 | t1,7{3,3,3,3,3,3,3,3,3} Bihexicated 10-simplex |
69300 | 4620 | |||||||||
| 27 | t2,7{3,3,3,3,3,3,3,3,3} Tripentellated 10-simplex |
138600 | 9240 | |||||||||
| 28 | t0,8{3,3,3,3,3,3,3,3,3} Octellated 10-simplex |
5940 | 495 | |||||||||
| 29 | t1,8{3,3,3,3,3,3,3,3,3} Biheptellated 10-simplex |
27720 | 1980 | |||||||||
| 30 | t0,9{3,3,3,3,3,3,3,3,3} ennicated 10-simplex |
990 | 110 | |||||||||
| 31 | t0,1,2,3,4,5,6,7,8,9{3,3,3,3,3,3,3,3,3} Omnitruncated 10-simplex |
199584000 | 39916800 |
The B10 family
There are 1023 forms based on all permutations of the Coxeter-Dynkin diagramCoxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
s with one or more rings.
Twelve cases are shown below: ten single-ring (rectified
Rectification (geometry)
In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
) forms, and two truncations. Bowers-style acronym names are given in parentheses for cross-referencing.
| # | Graph | Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... Schläfli symbol Name |
Element counts | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9-faces | 8-faces | 7-faces | 6-faces | 5-faces | 4-faces | Cells | Faces | Edges | Vertices | |||
| 1 | t0{4,3,3,3,3,3,3,3,3} 10-cube 10-cube In geometry, a 10-cube is a ten-dimensional hypercube. It has 1024 vertices, 5120 edges, 11520 square faces, 15360 cubic cells, 13440 tesseract 4-faces, 8064 5-cube 5-faces, 3360 6-cube 6-faces, 960 7-cube 7-faces, 180 8-cube 8-faces, and 20 9-cube 9-faces.... (deker) |
20 | 180 | 960 | 3360 | 8064 | 13440 | 15360 | 11520 | 5120 | 1024 | |
| 2 | t0,1{4,3,3,3,3,3,3,3,3} Truncated 10-cube (tade) |
51200 | 10240 | |||||||||
| 3 | t1{4,3,3,3,3,3,3,3,3} Rectified 10-cube Rectified 10-cube In ten-dimensional geometry, a rectified 10-cube is a convex uniform 10-polytope, being a rectification of the regular 10-cube.There are 10 rectifications of the 10-cube, with the zeroth being the 10-cube itself. Vertices of the rectified 10-cube are located at the edge-centers of the 10-cube... (rade) |
46080 | 5120 | |||||||||
| 4 | t2{4,3,3,3,3,3,3,3,3} Birectified 10-cube (brade) |
184320 | 11520 | |||||||||
| 5 | t3{4,3,3,3,3,3,3,3,3} Trirectified 10-cube (trade) |
322560 | 15360 | |||||||||
| 6 | t4{4,3,3,3,3,3,3,3,3} Quadrirectified 10-cube (terade) |
322560 | 13440 | |||||||||
| 7 | t4{3,3,3,3,3,3,3,3,4} Quadrirectified 10-orthoplex (terake) |
201600 | 8064 | |||||||||
| 8 | t3{3,3,3,3,3,3,3,4} Trirectified 10-orthoplex (trake) |
80640 | 3360 | |||||||||
| 9 | t2{3,3,3,3,3,3,3,3,4} Birectified 10-orthoplex (brake) |
20160 | 960 | |||||||||
| 10 | t1{3,3,3,3,3,3,3,3,4} Rectified 10-orthoplex Rectified 10-orthoplex In ten-dimensional geometry, a rectified 10-orthoplex is a convex uniform 10-polytope, being a rectification of the regular 10-orthoplex.There are 10 rectifications of the 10-orthoplex. Vertices of the rectified 10-orthoplex are located at the edge-centers of the 9-orthoplex. Vertices of the... (rake) |
2880 | 180 | |||||||||
| 11 | t0,1{3,3,3,3,3,3,3,3,4} Truncated 10-orthoplex (take) |
3060 | 360 | |||||||||
| 12 | t0{3,3,3,3,3,3,3,3,4} 10-orthoplex (ka) |
1024 | 5120 | 11520 | 15360 | 13440 | 8064 | 3360 | 960 | 180 | 20 |
The D10 family
The D10 family has symmetry of order 1,857,945,600 (10 factorialFactorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
x 29).
This family has 3×256−1=767 Wythoffian uniform polytopes, generated by marking one or more nodes of the D10 Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
. Of these, 511 (2×256−1) are repeated from the B10 family and 256 are unique to this family, with 2 listed below. Bowers-style acronym names are given in parentheses for cross-referencing.
| # | Graph | Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... Schläfli symbol Name |
Element counts | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9-faces | 8-faces | 7-faces | 6-faces | 5-faces | 4-faces | Cells | Faces | Edges | Vertices | |||
| 1 | 10-demicube 10-demicube In geometry, a demidekeract or 10-demicube is a uniform 10-polytope, constructed from the 10-cube with alternated vertices deleted. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes.... (hede) |
532 | 5300 | 24000 | 64800 | 115584 | 142464 | 122880 | 61440 | 11520 | 512 | |
| 2 | Truncated 10-demicube (thede) |
195840 | 23040 |
Regular and uniform honeycombs
There are four fundamental affine Coxeter groups that generate regular and uniform tessellations in 9-space:| # | Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
|---|---|---|---|
| 1 | 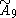 |
[3[10]] | |
| 2 | 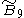 |
[4,37,4] | |
| 3 | 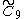 |
h[4,37,4] [4,36,31,1] |
|
| 4 | 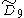 |
q[4,37,4] [31,1,35,31,1] |
Regular and uniform tessellations include:
- Regular 9-hypercubic honeycomb, with symbols {4,37,4},
- Uniform alternated 9-hypercubic honeycomb with symbols h{4,37,4},
Regular and uniform hyperbolic honeycombs
There are no compact hyperbolic Coxeter groups of rank 10, groups that can generate honeycombs with all finite facets, and a finite vertex figureVertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
. However there are 3 noncompact hyperbolic Coxeter groups of rank 9, each generating uniform honeycombs in 9-space as permutations of rings of the Coxeter diagrams.
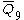 = [31,1,34,32,1]: = [31,1,34,32,1]: |
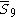 = [4,35,32,1]: = [4,35,32,1]: |
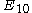 or or 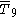 = [36,2,1]: = [36,2,1]: |
Three honeycombs from the
 family, generated by end-ringed Coxeter diagrams are:
family, generated by end-ringed Coxeter diagrams are:
- 621 honeycomb:
- 261 honeycomb:
- 162 honeycomb:
External links
- Polytope names
- Polytopes of Various Dimensions, Jonathan Bowers
- Multi-dimensional Glossary

