
9-polytope
Encyclopedia
9-simplex |
Rectified 9-simplex Rectified 9-simplex In nine-dimensional geometry, a rectified 9-simplex is a convex uniform 9-polytope, being a rectification of the regular 9-simplex.These polytopes are part of a family of 271 uniform 9-polytopes with A9 symmetry.... |
||||||||||
Truncated 9-simplex |
Cantellated 9-simplex |
||||||||||
Runcinated 9-simplex |
Stericated 9-simplex |
||||||||||
Pentellated 9-simplex |
Hexicated 9-simplex |
||||||||||
Heptellated 9-simplex |
Octellated 9-simplex |
||||||||||
9-orthoplex |
9-cube |
||||||||||
Truncated 9-orthoplex |
Truncated 9-cube |
||||||||||
Rectified 9-orthoplex Rectified 9-orthoplex In nine-dimensional geometry, a rectified 9-simplex is a convex uniform 9-polytope, being a rectification of the regular 9-orthoplex.There are 9 rectifications of the 9-orthoplex. Vertices of the rectified 9-orthoplex are located at the edge-centers of the 9-orthoplex. Vertices of the birectified... |
Rectified 9-cube Rectified 9-cube In nine-dimensional geometry, a rectified 9-cube is a convex uniform 9-polytope, being a rectification of the regular 9-cube.There are 9 rectifications of the 9-cube. The zeroth is the 9-cube itself, and the 8th is the dual 9-orthoplex. Vertices of the rectified 9-cube are located at the... |
||||||||||
9-demicube |
Truncated 9-demicube |
||||||||||
In nine-dimensional geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a polyyotton (or 9-polytope) is a polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
contained by 8-polytope facets. Each 7-polytope
7-polytope
In seven-dimensional geometry, a 7-polytope is a polytope contained by 6-polytope facets. Each 5-polytope ridge being shared by exactly two 6-polytope facets....
ridge
Ridge (geometry)
In geometry, a ridge is an -dimensional element of an n-dimensional polytope. It is also sometimes called a subfacet for having one lower dimension than a facet.By dimension, this corresponds to:*a vertex of a polygon;...
being shared by exactly two 8-polytope
8-polytope
In eight-dimensional geometry, a polyzetton is a polytope contained by 7-polytope facets. Each 6-polytope ridge being shared by exactly two 7-polytope facets....
facets
Facet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
.
A uniform polyyotton is one which is vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
, and constructed from uniform facets.
A proposed name for 9-polytope is polyyotton (plural: polyyotta), created from poly-, yotta-
Yotta
Yotta is the largest unit prefix in the International System of Units denoting a factor of 1024 or . It has the unit symbol Y.The prefix name is derived from the Greek , meaning eight, because it is equal to 10008...
(a variation on octa
Numerical prefix
Number prefixes are prefixes derived from numbers or numerals. In English and other European languages, they are used to coin numerous series of words, such as unicycle – bicycle – tricycle, dyad – triad – decade, biped – quadruped, September – October – November – December, decimal – hexadecimal,...
, meaning eight) and -on.
Regular 9-polytopes
Regular 9-polytopes can be represented by the Schläfli symbol {p,q,r,s,t,u,v,w}, with w {p,q,r,s,t,u,v} 8-polytope facetsFacet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
around each peak
Peak (geometry)
In geometry, a peak is an -face of an n-dimensional polytope. A peak attaches at least three facets ....
.
There are exactly three such convex regular 9-polytopes:
- {3,3,3,3,3,3,3,3} - 9-simplex
- {4,3,3,3,3,3,3,3} - 9-cube
- {3,3,3,3,3,3,3,4} - 9-orthoplex
There are no nonconvex regular 9-polytopes.
Euler characteristic
The Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
for 9-polytopes that are topological 8-spheres (including all convex 9-polytopes) is zero. χ=V-E+F-C+f4-f5+f6-f7+f8=2.
Uniform 9-polytopes by fundamental Coxeter groups
Uniform 9-polytopes with reflective symmetry can be generated by these three Coxeter groups, represented by permutations of rings of the Coxeter-Dynkin diagramCoxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
s:
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
|---|---|---|
| A9 | [38] | |
| B9 | [4,37] | |
| D9 | [36,1,1] |
Selected regular and uniform 9-polytopes from each family include:
- SimplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
family: A9 [38] -- 271 uniform 9-polytopes as permutations of rings in the group diagram, including one regular:
- {38} - 9-simplex or deca-9-tope or decayotton -
- 271 uniform 9-polytopes as permutations of rings in the group diagram, including one regular:
- HypercubeHypercubeIn geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
/orthoplex family: B9 [4,38] -- 511 uniform 9-polytopes as permutations of rings in the group diagram, including two regular ones:
- {4,37} - 9-cube or enneract -
- {37,4} - 9-orthoplex or enneacross -
- 511 uniform 9-polytopes as permutations of rings in the group diagram, including two regular ones:
- Demihypercube D9 family: [36,1,1] -
- 383 uniform 9-polytope as permutations of rings in the group diagram, including:
- {31,6,1} - 9-demicube or demienneract, 16,1 - ; also as h{4,38} .
- {36,1,1} - 9-orthoplex, 61,1 -
- 383 uniform 9-polytope as permutations of rings in the group diagram, including:
The A9 family
The A9 family has symmetry of order 3628800 (10 factorial).There are 256+16-1=271 forms based on all permutations of the Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
s with one or more rings. These are all enumerated below. Bowers-style acronym names are given in parentheses for cross-referencing.
| # | Graph | Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... Schläfli symbol Name |
Element counts | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 8-faces | 7-faces | 6-faces | 5-faces | 4-faces | Cells | Faces | Edges | Vertices | |||
| 1 | t0{3,3,3,3,3,3,3,3} 9-simplex (day) |
10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | |
| 2 | t1{3,3,3,3,3,3,3,3} Rectified 9-simplex Rectified 9-simplex In nine-dimensional geometry, a rectified 9-simplex is a convex uniform 9-polytope, being a rectification of the regular 9-simplex.These polytopes are part of a family of 271 uniform 9-polytopes with A9 symmetry.... (reday) |
360 | 45 | ||||||||
| 3 | t2{3,3,3,3,3,3,3,3} Birectified 9-simplex (breday) |
1260 | 120 | ||||||||
| 4 | t3{3,3,3,3,3,3,3,3} Trirectified 9-simplex (treday) |
2520 | 210 | ||||||||
| 5 | t4{3,3,3,3,3,3,3,3} Quadrirectified 9-simplex (icoy) |
3150 | 252 | ||||||||
| 6 | t0,1{3,3,3,3,3,3,3,3} Truncated 9-simplex (teday) |
405 | 90 | ||||||||
| 7 | t0,2{3,3,3,3,3,3,3,3} Cantellated 9-simplex |
2880 | 360 | ||||||||
| 8 | t1,2{3,3,3,3,3,3,3,3} Bitruncated 9-simplex |
1620 | 360 | ||||||||
| 9 | t0,3{3,3,3,3,3,3,3,3} Runcinated 9-simplex |
8820 | 840 | ||||||||
| 10 | t1,3{3,3,3,3,3,3,3,3} Bicantellated 9-simplex |
10080 | 1260 | ||||||||
| 11 | t2,3{3,3,3,3,3,3,3,3} Tritruncated 9-simplex (treday) |
3780 | 840 | ||||||||
| 12 | t0,4{3,3,3,3,3,3,3,3} Stericated 9-simplex |
15120 | 1260 | ||||||||
| 13 | t1,4{3,3,3,3,3,3,3,3} Biruncinated 9-simplex |
26460 | 2520 | ||||||||
| 14 | t2,4{3,3,3,3,3,3,3,3} Tricantellated 9-simplex |
20160 | 2520 | ||||||||
| 15 | t3,4{3,3,3,3,3,3,3,3} Quadritruncated 9-simplex |
5670 | 1260 | ||||||||
| 16 | t0,5{3,3,3,3,3,3,3,3} Pentellated 9-simplex |
15750 | 1260 | ||||||||
| 17 | t1,5{3,3,3,3,3,3,3,3} Bistericated 9-simplex |
37800 | 3150 | ||||||||
| 18 | t2,5{3,3,3,3,3,3,3,3} Triruncinated 9-simplex |
44100 | 4200 | ||||||||
| 19 | t3,5{3,3,3,3,3,3,3,3} Quadricantellated 9-simplex |
25200 | 3150 | ||||||||
| 20 | t0,6{3,3,3,3,3,3,3,3} Hexicated 9-simplex |
10080 | 840 | ||||||||
| 21 | t1,6{3,3,3,3,3,3,3,3} Bipentellated 9-simplex |
31500 | 2520 | ||||||||
| 22 | t2,6{3,3,3,3,3,3,3,3} Tristericated 9-simplex |
50400 | 4200 | ||||||||
| 23 | t0,7{3,3,3,3,3,3,3,3} Heptellated 9-simplex |
3780 | 360 | ||||||||
| 24 | t1,7{3,3,3,3,3,3,3,3} Bihexicated 9-simplex |
15120 | 1260 | ||||||||
| 25 | t0,8{3,3,3,3,3,3,3,3} Octellated 9-simplex |
720 | 90 | ||||||||
| 26 | t0,1,2{3,3,3,3,3,3,3,3} Cantitruncated 9-simplex |
3240 | 720 | ||||||||
| 27 | t0,1,3{3,3,3,3,3,3,3,3} Runcitruncated 9-simplex |
18900 | 2520 | ||||||||
| 28 | t0,2,3{3,3,3,3,3,3,3,3} Runcicantellated 9-simplex |
12600 | 2520 | ||||||||
| 29 | t1,2,3{3,3,3,3,3,3,3,3} Bicantitruncated 9-simplex |
11340 | 2520 | ||||||||
| 30 | t0,1,4{3,3,3,3,3,3,3,3} Steritruncated 9-simplex |
47880 | 5040 | ||||||||
| 31 | t0,2,4{3,3,3,3,3,3,3,3} Stericantellated 9-simplex |
60480 | 7560 | ||||||||
| 32 | t1,2,4{3,3,3,3,3,3,3,3} Biruncitruncated 9-simplex |
52920 | 7560 | ||||||||
| 33 | t0,3,4{3,3,3,3,3,3,3,3} Steriruncinated 9-simplex |
27720 | 5040 | ||||||||
| 34 | t1,3,4{3,3,3,3,3,3,3,3} Biruncicantellated 9-simplex |
41580 | 7560 | ||||||||
| 35 | t2,3,4{3,3,3,3,3,3,3,3} Tricantitruncated 9-simplex |
22680 | 5040 | ||||||||
| 36 | t0,1,5{3,3,3,3,3,3,3,3} Pentitruncated 9-simplex |
66150 | 6300 | ||||||||
| 37 | t0,2,5{3,3,3,3,3,3,3,3} Penticantellated 9-simplex |
126000 | 12600 | ||||||||
| 38 | t1,2,5{3,3,3,3,3,3,3,3} Bisteritruncated 9-simplex |
107100 | 12600 | ||||||||
| 39 | t0,3,5{3,3,3,3,3,3,3,3} Pentiruncinated 9-simplex |
107100 | 12600 | ||||||||
| 40 | t1,3,5{3,3,3,3,3,3,3,3} Bistericantellated 9-simplex |
151200 | 18900 | ||||||||
| 41 | t2,3,5{3,3,3,3,3,3,3,3} Triruncitruncated 9-simplex |
81900 | 12600 | ||||||||
| 42 | t0,4,5{3,3,3,3,3,3,3,3} Pentistericated 9-simplex |
37800 | 6300 | ||||||||
| 43 | t1,4,5{3,3,3,3,3,3,3,3} Bisteriruncinated 9-simplex |
81900 | 12600 | ||||||||
| 44 | t2,4,5{3,3,3,3,3,3,3,3} Triruncicantellated 9-simplex |
75600 | 12600 | ||||||||
| 45 | t3,4,5{3,3,3,3,3,3,3,3} Quadricantitruncated 9-simplex |
28350 | 6300 | ||||||||
| 46 | t0,1,6{3,3,3,3,3,3,3,3} Hexitruncated 9-simplex |
52920 | 5040 | ||||||||
| 47 | t0,2,6{3,3,3,3,3,3,3,3} Hexicantellated 9-simplex |
138600 | 12600 | ||||||||
| 48 | t1,2,6{3,3,3,3,3,3,3,3} Bipentitruncated 9-simplex |
113400 | 12600 | ||||||||
| 49 | t0,3,6{3,3,3,3,3,3,3,3} Hexiruncinated 9-simplex |
176400 | 16800 | ||||||||
| 50 | t1,3,6{3,3,3,3,3,3,3,3} Bipenticantellated 9-simplex |
239400 | 25200 | ||||||||
| 51 | t2,3,6{3,3,3,3,3,3,3,3} Tristeritruncated 9-simplex |
126000 | 16800 | ||||||||
| 52 | t0,4,6{3,3,3,3,3,3,3,3} Hexistericated 9-simplex |
113400 | 12600 | ||||||||
| 53 | t1,4,6{3,3,3,3,3,3,3,3} Bipentiruncinated 9-simplex |
226800 | 25200 | ||||||||
| 54 | t2,4,6{3,3,3,3,3,3,3,3} Tristericantellated 9-simplex |
201600 | 25200 | ||||||||
| 55 | t0,5,6{3,3,3,3,3,3,3,3} Hexipentellated 9-simplex |
32760 | 5040 | ||||||||
| 56 | t1,5,6{3,3,3,3,3,3,3,3} Bipentistericated 9-simplex |
94500 | 12600 | ||||||||
| 57 | t0,1,7{3,3,3,3,3,3,3,3} Heptitruncated 9-simplex |
23940 | 2520 | ||||||||
| 58 | t0,2,7{3,3,3,3,3,3,3,3} Hepticantellated 9-simplex |
83160 | 7560 | ||||||||
| 59 | t1,2,7{3,3,3,3,3,3,3,3} Bihexitruncated 9-simplex |
64260 | 7560 | ||||||||
| 60 | t0,3,7{3,3,3,3,3,3,3,3} Heptiruncinated 9-simplex |
144900 | 12600 | ||||||||
| 61 | t1,3,7{3,3,3,3,3,3,3,3} Bihexicantellated 9-simplex |
189000 | 18900 | ||||||||
| 62 | t0,4,7{3,3,3,3,3,3,3,3} Heptistericated 9-simplex |
138600 | 12600 | ||||||||
| 63 | t1,4,7{3,3,3,3,3,3,3,3} Bihexiruncinated 9-simplex |
264600 | 25200 | ||||||||
| 64 | t0,5,7{3,3,3,3,3,3,3,3} Heptipentellated 9-simplex |
71820 | 7560 | ||||||||
| 65 | t0,6,7{3,3,3,3,3,3,3,3} Heptihexicated 9-simplex |
17640 | 2520 | ||||||||
| 66 | t0,1,8{3,3,3,3,3,3,3,3} Octitruncated 9-simplex |
5400 | 720 | ||||||||
| 67 | t0,2,8{3,3,3,3,3,3,3,3} Octicantellated 9-simplex |
25200 | 2520 | ||||||||
| 68 | t0,3,8{3,3,3,3,3,3,3,3} Octiruncinated 9-simplex |
57960 | 5040 | ||||||||
| 69 | t0,4,8{3,3,3,3,3,3,3,3} Octistericated 9-simplex |
75600 | 6300 | ||||||||
| 70 | t0,1,2,3{3,3,3,3,3,3,3,3} Runcicantitruncated 9-simplex |
22680 | 5040 | ||||||||
| 71 | t0,1,2,4{3,3,3,3,3,3,3,3} Stericantitruncated 9-simplex |
105840 | 15120 | ||||||||
| 72 | t0,1,3,4{3,3,3,3,3,3,3,3} Steriruncitruncated 9-simplex |
75600 | 15120 | ||||||||
| 73 | t0,2,3,4{3,3,3,3,3,3,3,3} Steriruncicantellated 9-simplex |
75600 | 15120 | ||||||||
| 74 | t1,2,3,4{3,3,3,3,3,3,3,3} Biruncicantitruncated 9-simplex |
68040 | 15120 | ||||||||
| 75 | t0,1,2,5{3,3,3,3,3,3,3,3} Penticantitruncated 9-simplex |
214200 | 25200 | ||||||||
| 76 | t0,1,3,5{3,3,3,3,3,3,3,3} Pentiruncitruncated 9-simplex |
283500 | 37800 | ||||||||
| 77 | t0,2,3,5{3,3,3,3,3,3,3,3} Pentiruncicantellated 9-simplex |
264600 | 37800 | ||||||||
| 78 | t1,2,3,5{3,3,3,3,3,3,3,3} Bistericantitruncated 9-simplex |
245700 | 37800 | ||||||||
| 79 | t0,1,4,5{3,3,3,3,3,3,3,3} Pentisteritruncated 9-simplex |
138600 | 25200 | ||||||||
| 80 | t0,2,4,5{3,3,3,3,3,3,3,3} Pentistericantellated 9-simplex |
226800 | 37800 | ||||||||
| 81 | t1,2,4,5{3,3,3,3,3,3,3,3} Bisteriruncitruncated 9-simplex |
189000 | 37800 | ||||||||
| 82 | t0,3,4,5{3,3,3,3,3,3,3,3} Pentisteriruncinated 9-simplex |
138600 | 25200 | ||||||||
| 83 | t1,3,4,5{3,3,3,3,3,3,3,3} Bisteriruncicantellated 9-simplex |
207900 | 37800 | ||||||||
| 84 | t2,3,4,5{3,3,3,3,3,3,3,3} Triruncicantitruncated 9-simplex |
113400 | 25200 | ||||||||
| 85 | t0,1,2,6{3,3,3,3,3,3,3,3} Hexicantitruncated 9-simplex |
226800 | 25200 | ||||||||
| 86 | t0,1,3,6{3,3,3,3,3,3,3,3} Hexiruncitruncated 9-simplex |
453600 | 50400 | ||||||||
| 87 | t0,2,3,6{3,3,3,3,3,3,3,3} Hexiruncicantellated 9-simplex |
403200 | 50400 | ||||||||
| 88 | t1,2,3,6{3,3,3,3,3,3,3,3} Bipenticantitruncated 9-simplex |
378000 | 50400 | ||||||||
| 89 | t0,1,4,6{3,3,3,3,3,3,3,3} Hexisteritruncated 9-simplex |
403200 | 50400 | ||||||||
| 90 | t0,2,4,6{3,3,3,3,3,3,3,3} Hexistericantellated 9-simplex |
604800 | 75600 | ||||||||
| 91 | t1,2,4,6{3,3,3,3,3,3,3,3} Bipentiruncitruncated 9-simplex |
529200 | 75600 | ||||||||
| 92 | t0,3,4,6{3,3,3,3,3,3,3,3} Hexisteriruncinated 9-simplex |
352800 | 50400 | ||||||||
| 93 | t1,3,4,6{3,3,3,3,3,3,3,3} Bipentiruncicantellated 9-simplex |
529200 | 75600 | ||||||||
| 94 | t2,3,4,6{3,3,3,3,3,3,3,3} Tristericantitruncated 9-simplex |
302400 | 50400 | ||||||||
| 95 | t0,1,5,6{3,3,3,3,3,3,3,3} Hexipentitruncated 9-simplex |
151200 | 25200 | ||||||||
| 96 | t0,2,5,6{3,3,3,3,3,3,3,3} Hexipenticantellated 9-simplex |
352800 | 50400 | ||||||||
| 97 | t1,2,5,6{3,3,3,3,3,3,3,3} Bipentisteritruncated 9-simplex |
277200 | 50400 | ||||||||
| 98 | t0,3,5,6{3,3,3,3,3,3,3,3} Hexipentiruncinated 9-simplex |
352800 | 50400 | ||||||||
| 99 | t1,3,5,6{3,3,3,3,3,3,3,3} Bipentistericantellated 9-simplex |
491400 | 75600 | ||||||||
| 100 | t2,3,5,6{3,3,3,3,3,3,3,3} Tristeriruncitruncated 9-simplex |
252000 | 50400 | ||||||||
| 101 | t0,4,5,6{3,3,3,3,3,3,3,3} Hexipentistericated 9-simplex |
151200 | 25200 | ||||||||
| 102 | t1,4,5,6{3,3,3,3,3,3,3,3} Bipentisteriruncinated 9-simplex |
327600 | 50400 | ||||||||
| 103 | t0,1,2,7{3,3,3,3,3,3,3,3} Hepticantitruncated 9-simplex |
128520 | 15120 | ||||||||
| 104 | t0,1,3,7{3,3,3,3,3,3,3,3} Heptiruncitruncated 9-simplex |
359100 | 37800 | ||||||||
| 105 | t0,2,3,7{3,3,3,3,3,3,3,3} Heptiruncicantellated 9-simplex |
302400 | 37800 | ||||||||
| 106 | t1,2,3,7{3,3,3,3,3,3,3,3} Bihexicantitruncated 9-simplex |
283500 | 37800 | ||||||||
| 107 | t0,1,4,7{3,3,3,3,3,3,3,3} Heptisteritruncated 9-simplex |
478800 | 50400 | ||||||||
| 108 | t0,2,4,7{3,3,3,3,3,3,3,3} Heptistericantellated 9-simplex |
680400 | 75600 | ||||||||
| 109 | t1,2,4,7{3,3,3,3,3,3,3,3} Bihexiruncitruncated 9-simplex |
604800 | 75600 | ||||||||
| 110 | t0,3,4,7{3,3,3,3,3,3,3,3} Heptisteriruncinated 9-simplex |
378000 | 50400 | ||||||||
| 111 | t1,3,4,7{3,3,3,3,3,3,3,3} Bihexiruncicantellated 9-simplex |
567000 | 75600 | ||||||||
| 112 | t0,1,5,7{3,3,3,3,3,3,3,3} Heptipentitruncated 9-simplex |
321300 | 37800 | ||||||||
| 113 | t0,2,5,7{3,3,3,3,3,3,3,3} Heptipenticantellated 9-simplex |
680400 | 75600 | ||||||||
| 114 | t1,2,5,7{3,3,3,3,3,3,3,3} Bihexisteritruncated 9-simplex |
567000 | 75600 | ||||||||
| 115 | t0,3,5,7{3,3,3,3,3,3,3,3} Heptipentiruncinated 9-simplex |
642600 | 75600 | ||||||||
| 116 | t1,3,5,7{3,3,3,3,3,3,3,3} Bihexistericantellated 9-simplex |
907200 | 113400 | ||||||||
| 117 | t0,4,5,7{3,3,3,3,3,3,3,3} Heptipentistericated 9-simplex |
264600 | 37800 | ||||||||
| 118 | t0,1,6,7{3,3,3,3,3,3,3,3} Heptihexitruncated 9-simplex |
98280 | 15120 | ||||||||
| 119 | t0,2,6,7{3,3,3,3,3,3,3,3} Heptihexicantellated 9-simplex |
302400 | 37800 | ||||||||
| 120 | t1,2,6,7{3,3,3,3,3,3,3,3} Bihexipentitruncated 9-simplex |
226800 | 37800 | ||||||||
| 121 | t0,3,6,7{3,3,3,3,3,3,3,3} Heptihexiruncinated 9-simplex |
428400 | 50400 | ||||||||
| 122 | t0,4,6,7{3,3,3,3,3,3,3,3} Heptihexistericated 9-simplex |
302400 | 37800 | ||||||||
| 123 | t0,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentellated 9-simplex |
98280 | 15120 | ||||||||
| 124 | t0,1,2,8{3,3,3,3,3,3,3,3} Octicantitruncated 9-simplex |
35280 | 5040 | ||||||||
| 125 | t0,1,3,8{3,3,3,3,3,3,3,3} Octiruncitruncated 9-simplex |
136080 | 15120 | ||||||||
| 126 | t0,2,3,8{3,3,3,3,3,3,3,3} Octiruncicantellated 9-simplex |
105840 | 15120 | ||||||||
| 127 | t0,1,4,8{3,3,3,3,3,3,3,3} Octisteritruncated 9-simplex |
252000 | 25200 | ||||||||
| 128 | t0,2,4,8{3,3,3,3,3,3,3,3} Octistericantellated 9-simplex |
340200 | 37800 | ||||||||
| 129 | t0,3,4,8{3,3,3,3,3,3,3,3} Octisteriruncinated 9-simplex |
176400 | 25200 | ||||||||
| 130 | t0,1,5,8{3,3,3,3,3,3,3,3} Octipentitruncated 9-simplex |
252000 | 25200 | ||||||||
| 131 | t0,2,5,8{3,3,3,3,3,3,3,3} Octipenticantellated 9-simplex |
504000 | 50400 | ||||||||
| 132 | t0,3,5,8{3,3,3,3,3,3,3,3} Octipentiruncinated 9-simplex |
453600 | 50400 | ||||||||
| 133 | t0,1,6,8{3,3,3,3,3,3,3,3} Octihexitruncated 9-simplex |
136080 | 15120 | ||||||||
| 134 | t0,2,6,8{3,3,3,3,3,3,3,3} Octihexicantellated 9-simplex |
378000 | 37800 | ||||||||
| 135 | t0,1,7,8{3,3,3,3,3,3,3,3} Octiheptitruncated 9-simplex |
35280 | 5040 | ||||||||
| 136 | t0,1,2,3,4{3,3,3,3,3,3,3,3} Steriruncicantitruncated 9-simplex |
136080 | 30240 | ||||||||
| 137 | t0,1,2,3,5{3,3,3,3,3,3,3,3} Pentiruncicantitruncated 9-simplex |
491400 | 75600 | ||||||||
| 138 | t0,1,2,4,5{3,3,3,3,3,3,3,3} Pentistericantitruncated 9-simplex |
378000 | 75600 | ||||||||
| 139 | t0,1,3,4,5{3,3,3,3,3,3,3,3} Pentisteriruncitruncated 9-simplex |
378000 | 75600 | ||||||||
| 140 | t0,2,3,4,5{3,3,3,3,3,3,3,3} Pentisteriruncicantellated 9-simplex |
378000 | 75600 | ||||||||
| 141 | t1,2,3,4,5{3,3,3,3,3,3,3,3} Bisteriruncicantitruncated 9-simplex |
340200 | 75600 | ||||||||
| 142 | t0,1,2,3,6{3,3,3,3,3,3,3,3} Hexiruncicantitruncated 9-simplex |
756000 | 100800 | ||||||||
| 143 | t0,1,2,4,6{3,3,3,3,3,3,3,3} Hexistericantitruncated 9-simplex |
1058400 | 151200 | ||||||||
| 144 | t0,1,3,4,6{3,3,3,3,3,3,3,3} Hexisteriruncitruncated 9-simplex |
982800 | 151200 | ||||||||
| 145 | t0,2,3,4,6{3,3,3,3,3,3,3,3} Hexisteriruncicantellated 9-simplex |
982800 | 151200 | ||||||||
| 146 | t1,2,3,4,6{3,3,3,3,3,3,3,3} Bipentiruncicantitruncated 9-simplex |
907200 | 151200 | ||||||||
| 147 | t0,1,2,5,6{3,3,3,3,3,3,3,3} Hexipenticantitruncated 9-simplex |
554400 | 100800 | ||||||||
| 148 | t0,1,3,5,6{3,3,3,3,3,3,3,3} Hexipentiruncitruncated 9-simplex |
907200 | 151200 | ||||||||
| 149 | t0,2,3,5,6{3,3,3,3,3,3,3,3} Hexipentiruncicantellated 9-simplex |
831600 | 151200 | ||||||||
| 150 | t1,2,3,5,6{3,3,3,3,3,3,3,3} Bipentistericantitruncated 9-simplex |
756000 | 151200 | ||||||||
| 151 | t0,1,4,5,6{3,3,3,3,3,3,3,3} Hexipentisteritruncated 9-simplex |
554400 | 100800 | ||||||||
| 152 | t0,2,4,5,6{3,3,3,3,3,3,3,3} Hexipentistericantellated 9-simplex |
907200 | 151200 | ||||||||
| 153 | t1,2,4,5,6{3,3,3,3,3,3,3,3} Bipentisteriruncitruncated 9-simplex |
756000 | 151200 | ||||||||
| 154 | t0,3,4,5,6{3,3,3,3,3,3,3,3} Hexipentisteriruncinated 9-simplex |
554400 | 100800 | ||||||||
| 155 | t1,3,4,5,6{3,3,3,3,3,3,3,3} Bipentisteriruncicantellated 9-simplex |
831600 | 151200 | ||||||||
| 156 | t2,3,4,5,6{3,3,3,3,3,3,3,3} Tristeriruncicantitruncated 9-simplex |
453600 | 100800 | ||||||||
| 157 | t0,1,2,3,7{3,3,3,3,3,3,3,3} Heptiruncicantitruncated 9-simplex |
567000 | 75600 | ||||||||
| 158 | t0,1,2,4,7{3,3,3,3,3,3,3,3} Heptistericantitruncated 9-simplex |
1209600 | 151200 | ||||||||
| 159 | t0,1,3,4,7{3,3,3,3,3,3,3,3} Heptisteriruncitruncated 9-simplex |
1058400 | 151200 | ||||||||
| 160 | t0,2,3,4,7{3,3,3,3,3,3,3,3} Heptisteriruncicantellated 9-simplex |
1058400 | 151200 | ||||||||
| 161 | t1,2,3,4,7{3,3,3,3,3,3,3,3} Bihexiruncicantitruncated 9-simplex |
982800 | 151200 | ||||||||
| 162 | t0,1,2,5,7{3,3,3,3,3,3,3,3} Heptipenticantitruncated 9-simplex |
1134000 | 151200 | ||||||||
| 163 | t0,1,3,5,7{3,3,3,3,3,3,3,3} Heptipentiruncitruncated 9-simplex |
1701000 | 226800 | ||||||||
| 164 | t0,2,3,5,7{3,3,3,3,3,3,3,3} Heptipentiruncicantellated 9-simplex |
1587600 | 226800 | ||||||||
| 165 | t1,2,3,5,7{3,3,3,3,3,3,3,3} Bihexistericantitruncated 9-simplex |
1474200 | 226800 | ||||||||
| 166 | t0,1,4,5,7{3,3,3,3,3,3,3,3} Heptipentisteritruncated 9-simplex |
982800 | 151200 | ||||||||
| 167 | t0,2,4,5,7{3,3,3,3,3,3,3,3} Heptipentistericantellated 9-simplex |
1587600 | 226800 | ||||||||
| 168 | t1,2,4,5,7{3,3,3,3,3,3,3,3} Bihexisteriruncitruncated 9-simplex |
1360800 | 226800 | ||||||||
| 169 | t0,3,4,5,7{3,3,3,3,3,3,3,3} Heptipentisteriruncinated 9-simplex |
982800 | 151200 | ||||||||
| 170 | t1,3,4,5,7{3,3,3,3,3,3,3,3} Bihexisteriruncicantellated 9-simplex |
1474200 | 226800 | ||||||||
| 171 | t0,1,2,6,7{3,3,3,3,3,3,3,3} Heptihexicantitruncated 9-simplex |
453600 | 75600 | ||||||||
| 172 | t0,1,3,6,7{3,3,3,3,3,3,3,3} Heptihexiruncitruncated 9-simplex |
1058400 | 151200 | ||||||||
| 173 | t0,2,3,6,7{3,3,3,3,3,3,3,3} Heptihexiruncicantellated 9-simplex |
907200 | 151200 | ||||||||
| 174 | t1,2,3,6,7{3,3,3,3,3,3,3,3} Bihexipenticantitruncated 9-simplex |
831600 | 151200 | ||||||||
| 175 | t0,1,4,6,7{3,3,3,3,3,3,3,3} Heptihexisteritruncated 9-simplex |
1058400 | 151200 | ||||||||
| 176 | t0,2,4,6,7{3,3,3,3,3,3,3,3} Heptihexistericantellated 9-simplex |
1587600 | 226800 | ||||||||
| 177 | t1,2,4,6,7{3,3,3,3,3,3,3,3} Bihexipentiruncitruncated 9-simplex |
1360800 | 226800 | ||||||||
| 178 | t0,3,4,6,7{3,3,3,3,3,3,3,3} Heptihexisteriruncinated 9-simplex |
907200 | 151200 | ||||||||
| 179 | t0,1,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentitruncated 9-simplex |
453600 | 75600 | ||||||||
| 180 | t0,2,5,6,7{3,3,3,3,3,3,3,3} Heptihexipenticantellated 9-simplex |
1058400 | 151200 | ||||||||
| 181 | t0,3,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentiruncinated 9-simplex |
1058400 | 151200 | ||||||||
| 182 | t0,4,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentistericated 9-simplex |
453600 | 75600 | ||||||||
| 183 | t0,1,2,3,8{3,3,3,3,3,3,3,3} Octiruncicantitruncated 9-simplex |
196560 | 30240 | ||||||||
| 184 | t0,1,2,4,8{3,3,3,3,3,3,3,3} Octistericantitruncated 9-simplex |
604800 | 75600 | ||||||||
| 185 | t0,1,3,4,8{3,3,3,3,3,3,3,3} Octisteriruncitruncated 9-simplex |
491400 | 75600 | ||||||||
| 186 | t0,2,3,4,8{3,3,3,3,3,3,3,3} Octisteriruncicantellated 9-simplex |
491400 | 75600 | ||||||||
| 187 | t0,1,2,5,8{3,3,3,3,3,3,3,3} Octipenticantitruncated 9-simplex |
856800 | 100800 | ||||||||
| 188 | t0,1,3,5,8{3,3,3,3,3,3,3,3} Octipentiruncitruncated 9-simplex |
1209600 | 151200 | ||||||||
| 189 | t0,2,3,5,8{3,3,3,3,3,3,3,3} Octipentiruncicantellated 9-simplex |
1134000 | 151200 | ||||||||
| 190 | t0,1,4,5,8{3,3,3,3,3,3,3,3} Octipentisteritruncated 9-simplex |
655200 | 100800 | ||||||||
| 191 | t0,2,4,5,8{3,3,3,3,3,3,3,3} Octipentistericantellated 9-simplex |
1058400 | 151200 | ||||||||
| 192 | t0,3,4,5,8{3,3,3,3,3,3,3,3} Octipentisteriruncinated 9-simplex |
655200 | 100800 | ||||||||
| 193 | t0,1,2,6,8{3,3,3,3,3,3,3,3} Octihexicantitruncated 9-simplex |
604800 | 75600 | ||||||||
| 194 | t0,1,3,6,8{3,3,3,3,3,3,3,3} Octihexiruncitruncated 9-simplex |
1285200 | 151200 | ||||||||
| 195 | t0,2,3,6,8{3,3,3,3,3,3,3,3} Octihexiruncicantellated 9-simplex |
1134000 | 151200 | ||||||||
| 196 | t0,1,4,6,8{3,3,3,3,3,3,3,3} Octihexisteritruncated 9-simplex |
1209600 | 151200 | ||||||||
| 197 | t0,2,4,6,8{3,3,3,3,3,3,3,3} Octihexistericantellated 9-simplex |
1814400 | 226800 | ||||||||
| 198 | t0,1,5,6,8{3,3,3,3,3,3,3,3} Octihexipentitruncated 9-simplex |
491400 | 75600 | ||||||||
| 199 | t0,1,2,7,8{3,3,3,3,3,3,3,3} Octihepticantitruncated 9-simplex |
196560 | 30240 | ||||||||
| 200 | t0,1,3,7,8{3,3,3,3,3,3,3,3} Octiheptiruncitruncated 9-simplex |
604800 | 75600 | ||||||||
| 201 | t0,1,4,7,8{3,3,3,3,3,3,3,3} Octiheptisteritruncated 9-simplex |
856800 | 100800 | ||||||||
| 202 | t0,1,2,3,4,5{3,3,3,3,3,3,3,3} Pentisteriruncicantitruncated 9-simplex |
680400 | 151200 | ||||||||
| 203 | t0,1,2,3,4,6{3,3,3,3,3,3,3,3} Hexisteriruncicantitruncated 9-simplex |
1814400 | 302400 | ||||||||
| 204 | t0,1,2,3,5,6{3,3,3,3,3,3,3,3} Hexipentiruncicantitruncated 9-simplex |
1512000 | 302400 | ||||||||
| 205 | t0,1,2,4,5,6{3,3,3,3,3,3,3,3} Hexipentistericantitruncated 9-simplex |
1512000 | 302400 | ||||||||
| 206 | t0,1,3,4,5,6{3,3,3,3,3,3,3,3} Hexipentisteriruncitruncated 9-simplex |
1512000 | 302400 | ||||||||
| 207 | t0,2,3,4,5,6{3,3,3,3,3,3,3,3} Hexipentisteriruncicantellated 9-simplex |
1512000 | 302400 | ||||||||
| 208 | t1,2,3,4,5,6{3,3,3,3,3,3,3,3} Bipentisteriruncicantitruncated 9-simplex |
1360800 | 302400 | ||||||||
| 209 | t0,1,2,3,4,7{3,3,3,3,3,3,3,3} Heptisteriruncicantitruncated 9-simplex |
1965600 | 302400 | ||||||||
| 210 | t0,1,2,3,5,7{3,3,3,3,3,3,3,3} Heptipentiruncicantitruncated 9-simplex |
2948400 | 453600 | ||||||||
| 211 | t0,1,2,4,5,7{3,3,3,3,3,3,3,3} Heptipentistericantitruncated 9-simplex |
2721600 | 453600 | ||||||||
| 212 | t0,1,3,4,5,7{3,3,3,3,3,3,3,3} Heptipentisteriruncitruncated 9-simplex |
2721600 | 453600 | ||||||||
| 213 | t0,2,3,4,5,7{3,3,3,3,3,3,3,3} Heptipentisteriruncicantellated 9-simplex |
2721600 | 453600 | ||||||||
| 214 | t1,2,3,4,5,7{3,3,3,3,3,3,3,3} Bihexisteriruncicantitruncated 9-simplex |
2494800 | 453600 | ||||||||
| 215 | t0,1,2,3,6,7{3,3,3,3,3,3,3,3} Heptihexiruncicantitruncated 9-simplex |
1663200 | 302400 | ||||||||
| 216 | t0,1,2,4,6,7{3,3,3,3,3,3,3,3} Heptihexistericantitruncated 9-simplex |
2721600 | 453600 | ||||||||
| 217 | t0,1,3,4,6,7{3,3,3,3,3,3,3,3} Heptihexisteriruncitruncated 9-simplex |
2494800 | 453600 | ||||||||
| 218 | t0,2,3,4,6,7{3,3,3,3,3,3,3,3} Heptihexisteriruncicantellated 9-simplex |
2494800 | 453600 | ||||||||
| 219 | t1,2,3,4,6,7{3,3,3,3,3,3,3,3} Bihexipentiruncicantitruncated 9-simplex |
2268000 | 453600 | ||||||||
| 220 | t0,1,2,5,6,7{3,3,3,3,3,3,3,3} Heptihexipenticantitruncated 9-simplex |
1663200 | 302400 | ||||||||
| 221 | t0,1,3,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentiruncitruncated 9-simplex |
2721600 | 453600 | ||||||||
| 222 | t0,2,3,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentiruncicantellated 9-simplex |
2494800 | 453600 | ||||||||
| 223 | t1,2,3,5,6,7{3,3,3,3,3,3,3,3} Bihexipentistericantitruncated 9-simplex |
2268000 | 453600 | ||||||||
| 224 | t0,1,4,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentisteritruncated 9-simplex |
1663200 | 302400 | ||||||||
| 225 | t0,2,4,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentistericantellated 9-simplex |
2721600 | 453600 | ||||||||
| 226 | t0,3,4,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentisteriruncinated 9-simplex |
1663200 | 302400 | ||||||||
| 227 | t0,1,2,3,4,8{3,3,3,3,3,3,3,3} Octisteriruncicantitruncated 9-simplex |
907200 | 151200 | ||||||||
| 228 | t0,1,2,3,5,8{3,3,3,3,3,3,3,3} Octipentiruncicantitruncated 9-simplex |
2116800 | 302400 | ||||||||
| 229 | t0,1,2,4,5,8{3,3,3,3,3,3,3,3} Octipentistericantitruncated 9-simplex |
1814400 | 302400 | ||||||||
| 230 | t0,1,3,4,5,8{3,3,3,3,3,3,3,3} Octipentisteriruncitruncated 9-simplex |
1814400 | 302400 | ||||||||
| 231 | t0,2,3,4,5,8{3,3,3,3,3,3,3,3} Octipentisteriruncicantellated 9-simplex |
1814400 | 302400 | ||||||||
| 232 | t0,1,2,3,6,8{3,3,3,3,3,3,3,3} Octihexiruncicantitruncated 9-simplex |
2116800 | 302400 | ||||||||
| 233 | t0,1,2,4,6,8{3,3,3,3,3,3,3,3} Octihexistericantitruncated 9-simplex |
3175200 | 453600 | ||||||||
| 234 | t0,1,3,4,6,8{3,3,3,3,3,3,3,3} Octihexisteriruncitruncated 9-simplex |
2948400 | 453600 | ||||||||
| 235 | t0,2,3,4,6,8{3,3,3,3,3,3,3,3} Octihexisteriruncicantellated 9-simplex |
2948400 | 453600 | ||||||||
| 236 | t0,1,2,5,6,8{3,3,3,3,3,3,3,3} Octihexipenticantitruncated 9-simplex |
1814400 | 302400 | ||||||||
| 237 | t0,1,3,5,6,8{3,3,3,3,3,3,3,3} Octihexipentiruncitruncated 9-simplex |
2948400 | 453600 | ||||||||
| 238 | t0,2,3,5,6,8{3,3,3,3,3,3,3,3} Octihexipentiruncicantellated 9-simplex |
2721600 | 453600 | ||||||||
| 239 | t0,1,4,5,6,8{3,3,3,3,3,3,3,3} Octihexipentisteritruncated 9-simplex |
1814400 | 302400 | ||||||||
| 240 | t0,1,2,3,7,8{3,3,3,3,3,3,3,3} Octiheptiruncicantitruncated 9-simplex |
907200 | 151200 | ||||||||
| 241 | t0,1,2,4,7,8{3,3,3,3,3,3,3,3} Octiheptistericantitruncated 9-simplex |
2116800 | 302400 | ||||||||
| 242 | t0,1,3,4,7,8{3,3,3,3,3,3,3,3} Octiheptisteriruncitruncated 9-simplex |
1814400 | 302400 | ||||||||
| 243 | t0,1,2,5,7,8{3,3,3,3,3,3,3,3} Octiheptipenticantitruncated 9-simplex |
2116800 | 302400 | ||||||||
| 244 | t0,1,3,5,7,8{3,3,3,3,3,3,3,3} Octiheptipentiruncitruncated 9-simplex |
3175200 | 453600 | ||||||||
| 245 | t0,1,2,6,7,8{3,3,3,3,3,3,3,3} Octiheptihexicantitruncated 9-simplex |
907200 | 151200 | ||||||||
| 246 | t0,1,2,3,4,5,6{3,3,3,3,3,3,3,3} Hexipentisteriruncicantitruncated 9-simplex |
2721600 | 604800 | ||||||||
| 247 | t0,1,2,3,4,5,7{3,3,3,3,3,3,3,3} Heptipentisteriruncicantitruncated 9-simplex |
4989600 | 907200 | ||||||||
| 248 | t0,1,2,3,4,6,7{3,3,3,3,3,3,3,3} Heptihexisteriruncicantitruncated 9-simplex |
4536000 | 907200 | ||||||||
| 249 | t0,1,2,3,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentiruncicantitruncated 9-simplex |
4536000 | 907200 | ||||||||
| 250 | t0,1,2,4,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentistericantitruncated 9-simplex |
4536000 | 907200 | ||||||||
| 251 | t0,1,3,4,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentisteriruncitruncated 9-simplex |
4536000 | 907200 | ||||||||
| 252 | t0,2,3,4,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentisteriruncicantellated 9-simplex |
4536000 | 907200 | ||||||||
| 253 | t1,2,3,4,5,6,7{3,3,3,3,3,3,3,3} Bihexipentisteriruncicantitruncated 9-simplex |
4082400 | 907200 | ||||||||
| 254 | t0,1,2,3,4,5,8{3,3,3,3,3,3,3,3} Octipentisteriruncicantitruncated 9-simplex |
3326400 | 604800 | ||||||||
| 255 | t0,1,2,3,4,6,8{3,3,3,3,3,3,3,3} Octihexisteriruncicantitruncated 9-simplex |
5443200 | 907200 | ||||||||
| 256 | t0,1,2,3,5,6,8{3,3,3,3,3,3,3,3} Octihexipentiruncicantitruncated 9-simplex |
4989600 | 907200 | ||||||||
| 257 | t0,1,2,4,5,6,8{3,3,3,3,3,3,3,3} Octihexipentistericantitruncated 9-simplex |
4989600 | 907200 | ||||||||
| 258 | t0,1,3,4,5,6,8{3,3,3,3,3,3,3,3} Octihexipentisteriruncitruncated 9-simplex |
4989600 | 907200 | ||||||||
| 259 | t0,2,3,4,5,6,8{3,3,3,3,3,3,3,3} Octihexipentisteriruncicantellated 9-simplex |
4989600 | 907200 | ||||||||
| 260 | t0,1,2,3,4,7,8{3,3,3,3,3,3,3,3} Octiheptisteriruncicantitruncated 9-simplex |
3326400 | 604800 | ||||||||
| 261 | t0,1,2,3,5,7,8{3,3,3,3,3,3,3,3} Octiheptipentiruncicantitruncated 9-simplex |
5443200 | 907200 | ||||||||
| 262 | t0,1,2,4,5,7,8{3,3,3,3,3,3,3,3} Octiheptipentistericantitruncated 9-simplex |
4989600 | 907200 | ||||||||
| 263 | t0,1,3,4,5,7,8{3,3,3,3,3,3,3,3} Octiheptipentisteriruncitruncated 9-simplex |
4989600 | 907200 | ||||||||
| 264 | t0,1,2,3,6,7,8{3,3,3,3,3,3,3,3} Octiheptihexiruncicantitruncated 9-simplex |
3326400 | 604800 | ||||||||
| 265 | t0,1,2,4,6,7,8{3,3,3,3,3,3,3,3} Octiheptihexistericantitruncated 9-simplex |
5443200 | 907200 | ||||||||
| 266 | t0,1,2,3,4,5,6,7{3,3,3,3,3,3,3,3} Heptihexipentisteriruncicantitruncated 9-simplex |
8164800 | 1814400 | ||||||||
| 267 | t0,1,2,3,4,5,6,8{3,3,3,3,3,3,3,3} Octihexipentisteriruncicantitruncated 9-simplex |
9072000 | 1814400 | ||||||||
| 268 | t0,1,2,3,4,5,7,8{3,3,3,3,3,3,3,3} Octiheptipentisteriruncicantitruncated 9-simplex |
9072000 | 1814400 | ||||||||
| 269 | t0,1,2,3,4,6,7,8{3,3,3,3,3,3,3,3} Octiheptihexisteriruncicantitruncated 9-simplex |
9072000 | 1814400 | ||||||||
| 270 | t0,1,2,3,5,6,7,8{3,3,3,3,3,3,3,3} Octiheptihexipentiruncicantitruncated 9-simplex |
9072000 | 1814400 | ||||||||
| 271 | t0,1,2,3,4,5,6,7,8{3,3,3,3,3,3,3,3} Omnitruncated 9-simplex |
16329600 | 3628800 |
The B9 family
There are 511 forms based on all permutations of the Coxeter-Dynkin diagramCoxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
s with one or more rings.
Eleven cases are shown below: Nine rectified
Rectification (geometry)
In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
forms and 2 truncations. Bowers-style acronym names are given in parentheses for cross-referencing. Bowers-style acronym names are given in parentheses for cross-referencing.
| # | Graph | Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... Schläfli symbol Name |
Element counts | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 8-faces | 7-faces | 6-faces | 5-faces | 4-faces | Cells | Faces | Edges | Vertices | |||
| 1 | t0{4,3,3,3,3,3,3,3} 9-cube (enne) |
18 | 144 | 672 | 2016 | 4032 | 5376 | 4608 | 2304 | 512 | |
| 2 | t0,1{4,3,3,3,3,3,3,3} Truncated 9-cube (ten) |
2304 | 4608 | ||||||||
| 3 | t1{4,3,3,3,3,3,3,3} Rectified 9-cube Rectified 9-cube In nine-dimensional geometry, a rectified 9-cube is a convex uniform 9-polytope, being a rectification of the regular 9-cube.There are 9 rectifications of the 9-cube. The zeroth is the 9-cube itself, and the 8th is the dual 9-orthoplex. Vertices of the rectified 9-cube are located at the... (ren) |
18432 | 2304 | ||||||||
| 4 | t2{4,3,3,3,3,3,3,3} Birectified 9-cube (barn) |
64512 | 4608 | ||||||||
| 5 | t3{4,3,3,3,3,3,3,3} Trirectified 9-cube (tarn) |
96768 | 5376 | ||||||||
| 6 | t4{4,3,3,3,3,3,3,3} Quadrirectified 9-cube (nav) (Quadrirectified 9-orthoplex) |
80640 | 4032 | ||||||||
| 7 | t3{3,3,3,3,3,3,3,4} Trirectified 9-orthoplex (tarv) |
40320 | 2016 | ||||||||
| 8 | t2{3,3,3,3,3,3,3,4} Birectified 9-orthoplex (brav) |
12096 | 672 | ||||||||
| 9 | t1{3,3,3,3,3,3,3,4} Rectified 9-orthoplex Rectified 9-orthoplex In nine-dimensional geometry, a rectified 9-simplex is a convex uniform 9-polytope, being a rectification of the regular 9-orthoplex.There are 9 rectifications of the 9-orthoplex. Vertices of the rectified 9-orthoplex are located at the edge-centers of the 9-orthoplex. Vertices of the birectified... (riv) |
2016 | 144 | ||||||||
| 10 | t0,1{3,3,3,3,3,3,3,4} Truncated 9-orthoplex (tiv) |
2160 | 288 | ||||||||
| 11 | t0{3,3,3,3,3,3,3,4} 9-orthoplex (vee) |
512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 |
The D9 family
The D9 family has symmetry of order 92,897,280 (9 factorialFactorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
× 28).
This family has 3×128−1=383 Wythoffian uniform polytopes, generated by marking one or more nodes of the D9 Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
. Of these, 255 (2×128−1) are repeated from the B9 family and 128 are unique to this family, with the eight 1 or 2 ringed forms listed below. Bowers-style acronym names are given in parentheses for cross-referencing.
| # | Coxeter plane graphs | Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... Schläfli symbol |
Base point (Alternately signed) |
Element counts | Circumrad | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B9 | D9 | D8 | D7 | D6 | D5 | D4 | D3 | A7 | A5 | A3 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | ||||
| 1 | 9-demicube (henne) |
(1,1,1,1,1,1,1,1,1) | 274 | 2448 | 9888 | 23520 | 36288 | 37632 | 21404 | 4608 | 256 | 1.0606601 | |||||||||||
| 2 | Truncated 9-demicube (thenne) |
(1,1,3,3,3,3,3,3,3) | 69120 | 9216 | 2.8504384 | ||||||||||||||||||
| 3 | Cantellated 9-demicube |
(1,1,1,3,3,3,3,3,3) | 225792 | 21504 | 2.6692696 | ||||||||||||||||||
| 4 | Runcinated 9-demicube |
(1,1,1,1,3,3,3,3,3) | 419328 | 32256 | 2.4748735 | ||||||||||||||||||
| 5 | Stericated 9-demicube |
(1,1,1,1,1,3,3,3,3) | 483840 | 32256 | 2.2638462 | ||||||||||||||||||
| 6 | Pentellated 9-demicube |
(1,1,1,1,1,1,3,3,3) | 354816 | 21504 | 2.0310094 | ||||||||||||||||||
| 7 | Hexicated 9-demicube |
(1,1,1,1,1,1,1,3,3) | 161280 | 9216 | 1.7677668 | ||||||||||||||||||
| 8 | Heptellated 9-demicube |
(1,1,1,1,1,1,1,1,3) | 41472 | 2304 | 1.4577379 |
Regular and uniform honeycombs
There are five fundamental affine Coxeter groups that generate regular and uniform tessellations in 8-space:| # | Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
|---|---|---|---|
| 1 | 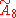 |
[3[8]] | |
| 2 | 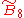 |
h[4,36,4] [4,35,31,1] |
|
| 3 | 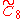 |
[4,36,4] | |
| 4 | 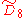 |
q[4,36,4] [31,1,34,31,1] |
|
| 5 |  |
[35,2,1] |
Regular and uniform tessellations include:
-
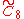 :
:
- Regular octeractic honeycomb: {4,36,4},
-
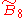 :
:
- Uniform demiocteractic honeycomb: h{4,36,4} or {31,1,35,4}, or
-
 :
:
- Uniform 521 honeycomb:
- Uniform 251 honeycombGosset 2 51 honeycombIn 8-dimensional geometry, the 251 honeycomb is a space-filling uniform tessellation. It is composed of 241 polytope and 8-simplex facets arranged in a demiocteract vertex figure...
: - Uniform 152 honeycombGosset 1 52 honeycombIn geometry, the 152 honeycomb is a uniform tessellation of 8-dimensional Euclidean space. It contains 142 and 151 facets, in a birectified 8-simplex vertex figure...
:
Regular and uniform hyperbolic honeycombs
There are no compact hyperbolic Coxeter groups of rank 9, groups that can generate honeycombs with all finite facets, and a finite vertex figureVertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
. However there are 4 noncompact hyperbolic Coxeter groups of rank 9, each generating uniform honeycombs in 8-space as permutations of rings of the Coxeter diagrams.
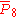 = [3,3[8]]: = [3,3[8]]: |
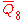 = [31,1,33,32,1]: = [31,1,33,32,1]: |
 = [4,34,32,1]: = [4,34,32,1]: |
 = [34,3,1]: = [34,3,1]: |
External links
- Polytope names
- Polytopes of Various Dimensions, Jonathan Bowers
- Multi-dimensional Glossary

