
10-cube
Encyclopedia
| 10-cube Dekeract |
|
|---|---|
Orthogonal projection inside Petrie polygon Petrie polygon In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets... Orange vertices are doubled, and central yellow one has four |
|
| Type | Regular 10-polytope 10-polytope In ten-dimensional geometry, a 10-polytope is a 10 dimensional polytope contained by 9-polytope facets. Each 8-polytope ridge being shared by exactly two 9-polytope facets.... |
| Family | hypercube Hypercube In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An... |
| Schläfli symbol | {4,38} |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
| 9-faces | 20 {4,37} |
| 8-faces | 180 {4,36} |
| 7-faces | 960 {4,35} |
| 6-faces | 3360 {4,34} |
| 5-faces | 8064 {4,33} |
| 4-faces | 13440 {4,3,3} Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8... |
| Cells | 15360 {4,3} Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
| Faces | 11520 squares Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... |
| Edges | 5120 |
| Vertices | 1024 |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
9-simplex |
| Petrie polygon Petrie polygon In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets... |
icosagon Icosagon In geometry, an icosagon is a twenty-sided polygon. The sum of any icosagon's interior angles is 3240 degrees.One interior angle in a regular icosagon is 162° meaning that one exterior angle would be 18°... |
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
C10, [38,4] |
| Dual | 10-orthoplex |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a 10-cube is a ten-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
. It has 1024 vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
, 5120 edge
Edge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
s, 11520 square faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
, 15360 cubic cells, 13440 tesseract
Tesseract
In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
4-faces
Hypercell
In geometry, a hypercell is a descriptive term for an element of a polytope or tessellation, usually representing an element one dimension higher than a cell. The most generally accepted term is 4-face because it contains a 4-dimensional interior...
, 8064 5-cube 5-faces, 3360 6-cube 6-faces, 960 7-cube 7-faces, 180 8-cube 8-faces, and 20 9-cube 9-faces.
It can be named by its Schläfli symbol {4,38}, being composed of 3 9-cubes around each 8-face. It is sometimes called a dekeract, the name derived from combining the name tesseract
Tesseract
In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
(the 4-cube) with deka- for ten (dimensions) in Greek
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
, It can also be called an icosaxennon or icosa-10-tope as a 10 dimensional polytope
10-polytope
In ten-dimensional geometry, a 10-polytope is a 10 dimensional polytope contained by 9-polytope facets. Each 8-polytope ridge being shared by exactly two 9-polytope facets....
, constructed from 20 regular facets.
It is a part of an infinite family of polytopes, called hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
s. The dual of an dekeract can be called a 10-orthoplex or decacross, and is a part of the infinite family of cross-polytope
Cross-polytope
In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices...
s.
Cartesian coordinates
Cartesian coordinates for the vertices of a dekeract centered at the origin and edge length 2 are- (±1,±1,±1,±1,±1,±1,±1,±1,±1,±1)
while the interior of the same consists of all points (x0, x1, x2, x3, x4, x5, x6, x7, x8, x9) with −1 < xi < 1.
Other images
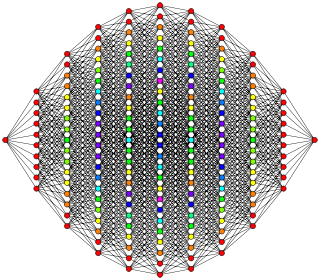 This 10-cube graph is an orthogonal projection. This oriention shows columns of vertices positioned a vertex-edge-vertex distance from one vertex on the left to one vertex on the right, and edges attaching adjacent columns of vertices. The number of vertices in each column represents rows in Pascal's triangle Pascal's triangle In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal... , being 1:10:45:120:210:252:210:120:45:10:1. |
 Petrie polygon, skew orthogonal projection |
Derived polytopes
Applying an alternation operation, deleting alternating vertices of the dekeract, creates another uniform polytopeUniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
, called a 10-demicube
10-demicube
In geometry, a demidekeract or 10-demicube is a uniform 10-polytope, constructed from the 10-cube with alternated vertices deleted. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes....
, (part of an infinite family called demihypercubes), which has 20 demiocteract
Demiocteract
In geometry, a demiocteract or 8-demicube is a uniform 8-polytope, constructed from the 8-hypercube, octeract, with alternated vertices deleted...
ic and 512 enneazettonic facets.
External links
- Multi-dimensional Glossary: hypercube Garrett Jones

