Zero sharp
Encyclopedia
In the mathematical discipline of set theory
, 0# (zero sharp, also 0#) is the set of true formulas about (order-)indiscernibles
in the Gödel constructible universe. It is often encoded as a subset of the integers (using Gödel numbering), or as a subset of the hereditarily finite set
s, or (somewhat misleadingly) as a real number
. Its existence is unprovable in ZFC, the standard form of axiomatic set theory, but follows from a suitable large cardinal axiom. It was first introduced as a set of formulas in Silver's
1966 thesis, later published as , where it was denoted by Σ, and rediscovered by , who considered it as a subset of the natural numbers and introduced the notation O# (with a capital letter O; this later changed to a number 0).
Roughly speaking, if 0# exists then the universe V of sets is much larger than the universe L of constructible sets, while if it does not exist then the universe of all sets is closely approximated by the constructible sets.
s of the true sentences about the constructible universe, with ci interpreted as the uncountable cardinal ℵi.
(Here ℵi means ℵi in the full universe, not the constructible universe.)
There is a subtlety about this definition: by Tarski's undefinability theorem it is not in general possible to define the truth of a formula of set theory in the language of set theory. To solve this, Silver and Solovay assumed the existence of a suitable large cardinal, such as a Ramsey cardinal
, and showed that with this extra assumption it is possible to define the truth of statements about the constructible universe. More generally, the definition of 0# works provided that there is an uncountable set of indiscernibles for some Lα, and the phrase "0# exists" is used as a shorthand way of saying this.
There are several minor variations of the definition of 0#, which make no significant difference to its properties. There are many different choices of Gödel numbering, and 0# depends on this choice. Instead of being considered as a subset of the natural numbers, it is also possible to encode 0# as a subset of formulas of a language, or as a subset of the hereditarily finite sets, or as a real number.
s implies the existence of 0#. This is close to being best possible, because the existence of 0# implies that in the constructible universe there is an α-Erdős cardinal for all countable α, so such cardinals cannot be used to prove the existence of 0#.
Chang's conjecture
implies the existence of 0#.
Donald A. Martin
and Leo Harrington
have shown that the existence of 0# is equivalent to the determinacy of lightface analytic games. In fact, the strategy for a universal lightface analytic game has the same Turing degree
as 0#.
It follows from Jensen's covering theorem
that the existence of 0# is equivalent to ωω being a regular cardinal
in the constructible universe L.
Silver showed that the existence of an uncountable set of indiscernibles in the constructible universe is equivalent to the existence of 0#.
cardinal
in the set-theoretic universe V is an indiscernible in L and satisfies all large cardinal axioms that are realized in L (such as being totally ineffable). It follows that the existence of 0# contradicts the axiom of constructibility
: V = L.
If 0# exists, then it is an example of a non-constuctible Δ set of integers. This is in some sense the simplest possibility for a non-constructible set, since all Σ and Π sets of integers are constructible.
On the other hand, if 0# does not exist, then the constructible universe L is the core model—that is, the canonical inner model that approximates the large cardinal structure of the universe considered. In that case, Jensen's covering lemma holds:
This deep result is due to Ronald Jensen
. Using forcing
it is easy to see that the condition that x is uncountable cannot be removed. For example, consider Namba forcing, that preserves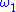
and collapses 
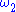to an ordinal of cofinality
. Let 
be an 
-sequence cofinal
on
and generic
over L. Then no set in L of L-size smaller than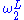
(which is uncountable in V, since 
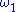is preserved) can cover 
, since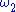 
is a regular
cardinal.
.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, 0# (zero sharp, also 0#) is the set of true formulas about (order-)indiscernibles
Indiscernibles
In mathematical logic, indiscernibles are objects which cannot be distinguished by any property or relation defined by a formula. Usually only first-order formulas are considered...
in the Gödel constructible universe. It is often encoded as a subset of the integers (using Gödel numbering), or as a subset of the hereditarily finite set
Hereditarily finite set
In mathematics and set theory, hereditarily finite sets are defined recursively as finite sets consisting of 0 or more hereditarily finite sets.-Formal definition:...
s, or (somewhat misleadingly) as a real number
Baire space (set theory)
In set theory, the Baire space is the set of all infinite sequences of natural numbers with a certain topology. This space is commonly used in descriptive set theory, to the extent that its elements are often called “reals.” It is often denoted B, N'N, or ωω...
. Its existence is unprovable in ZFC, the standard form of axiomatic set theory, but follows from a suitable large cardinal axiom. It was first introduced as a set of formulas in Silver's
Jack Silver
Jack Howard Silver is a set theorist and logician at the University of California, Berkeley. He has made several deep contributions to set theory...
1966 thesis, later published as , where it was denoted by Σ, and rediscovered by , who considered it as a subset of the natural numbers and introduced the notation O# (with a capital letter O; this later changed to a number 0).
Roughly speaking, if 0# exists then the universe V of sets is much larger than the universe L of constructible sets, while if it does not exist then the universe of all sets is closely approximated by the constructible sets.
Definition
Zero sharp was defined by Silver and Solovay as follows. Consider the language of set theory with extra constant symbols c1, c2, ... for each positive integer. Then 0# is defined to be the set of Gödel numberGödel number
In mathematical logic, a Gödel numbering is a function that assigns to each symbol and well-formed formula of some formal language a unique natural number, called its Gödel number. The concept was famously used by Kurt Gödel for the proof of his incompleteness theorems...
s of the true sentences about the constructible universe, with ci interpreted as the uncountable cardinal ℵi.
(Here ℵi means ℵi in the full universe, not the constructible universe.)
There is a subtlety about this definition: by Tarski's undefinability theorem it is not in general possible to define the truth of a formula of set theory in the language of set theory. To solve this, Silver and Solovay assumed the existence of a suitable large cardinal, such as a Ramsey cardinal
Ramsey cardinal
In mathematics, a Ramsey cardinal is a certain kind of large cardinal number introduced by and named after Frank P. Ramsey.With [κ]<ω denoting the set of all finite subsets of κ, a cardinal number κ such that for every function...
, and showed that with this extra assumption it is possible to define the truth of statements about the constructible universe. More generally, the definition of 0# works provided that there is an uncountable set of indiscernibles for some Lα, and the phrase "0# exists" is used as a shorthand way of saying this.
There are several minor variations of the definition of 0#, which make no significant difference to its properties. There are many different choices of Gödel numbering, and 0# depends on this choice. Instead of being considered as a subset of the natural numbers, it is also possible to encode 0# as a subset of formulas of a language, or as a subset of the hereditarily finite sets, or as a real number.
Statements that imply the existence of 0#
The condition about the existence of a Ramsey cardinal implying that 0# exists can be weakened. The existence of ω1-Erdős cardinalErdos cardinal
In mathematics, an Erdős cardinal, also called a partition cardinal is a certain kind of large cardinal number introduced by .The Erdős cardinal κ is defined to be the least cardinal such that for every function...
s implies the existence of 0#. This is close to being best possible, because the existence of 0# implies that in the constructible universe there is an α-Erdős cardinal for all countable α, so such cardinals cannot be used to prove the existence of 0#.
Chang's conjecture
Chang's conjecture
In model theory, a branch of mathematical logic, Chang's conjecture, attributed to Chen Chung Chang by , states that every model of type for a countable language has an elementary submodel of type . A model is of type if it is of cardinality α and a unary relation is represented by a subset of...
implies the existence of 0#.
Statements equivalent to existence of 0#
Kunen showed that 0# exists if and only if there exists a non-trivial elementary embedding for the Gödel constructible universe L into itself.Donald A. Martin
Donald A. Martin
Donald A. Martin is a set theorist and philosopher of mathematics at UCLA, where he is a member of the faculty of mathematics and philosophy....
and Leo Harrington
Leo Harrington
Leo Anthony Harrington is a professor of mathematics at the University of California, Berkeley who works inrecursion theory, model theory, and set theory.* Harrington and Jeff Paris proved the Paris–Harrington theorem....
have shown that the existence of 0# is equivalent to the determinacy of lightface analytic games. In fact, the strategy for a universal lightface analytic game has the same Turing degree
Turing degree
In computer science and mathematical logic the Turing degree or degree of unsolvability of a set of natural numbers measures the level of algorithmic unsolvability of the set...
as 0#.
It follows from Jensen's covering theorem
Jensen's covering theorem
In set theory, Jensen's covering theorem states that if 0# does not exist then every uncountable set of ordinals is contained in a constructible set of the same cardinality. Informally this conclusion says that the constructible universe is close to the universe of all sets. The first proof ...
that the existence of 0# is equivalent to ωω being a regular cardinal
Regular cardinal
In set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
in the constructible universe L.
Silver showed that the existence of an uncountable set of indiscernibles in the constructible universe is equivalent to the existence of 0#.
Consequences of existence and non-existence
Its existence implies that every uncountableUncountable set
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
cardinal
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
in the set-theoretic universe V is an indiscernible in L and satisfies all large cardinal axioms that are realized in L (such as being totally ineffable). It follows that the existence of 0# contradicts the axiom of constructibility
Axiom of constructibility
The axiom of constructibility is a possible axiom for set theory in mathematics that asserts that every set is constructible. The axiom is usually written as V = L, where V and L denote the von Neumann universe and the constructible universe, respectively.- Implications :The axiom of...
: V = L.
If 0# exists, then it is an example of a non-constuctible Δ set of integers. This is in some sense the simplest possibility for a non-constructible set, since all Σ and Π sets of integers are constructible.
On the other hand, if 0# does not exist, then the constructible universe L is the core model—that is, the canonical inner model that approximates the large cardinal structure of the universe considered. In that case, Jensen's covering lemma holds:
- For every uncountable set x of ordinals there is a constructible y such that x ⊂ y and y has the same cardinality as x.
This deep result is due to Ronald Jensen
Ronald Jensen
Ronald Björn Jensen is an American mathematician active in Europe, primarily known for his work in mathematical logic and set theory.-Career:...
. Using forcing
Forcing (mathematics)
In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...
it is easy to see that the condition that x is uncountable cannot be removed. For example, consider Namba forcing, that preserves
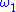and collapses 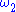to an ordinal of cofinalityCofinality
In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
. Let be an -sequence cofinalCofinal (mathematics)
In mathematics, let A be a set and let ≤ be a binary relation on A. Then a subset B of A is said to be cofinal if it satisfies the following condition:This definition is most commonly applied when A is a partially ordered set or directed set under the relation ≤. Also, the notion of cofinal...
on
and genericGeneric filter
In the mathematical field of set theory, a generic filter is a kind of object used in the theory of forcing, a technique used for many purposes, but especially to establish the independence of certain propositions from certain formal theories, such as ZFC...
over L. Then no set in L of L-size smaller than
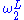(which is uncountable in V, since 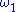is preserved) can cover , since 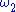is a regularRegular cardinal
In set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
cardinal.
Other sharps
If x is any set, then x# is defined analogously to 0# except that one uses L[x] instead of L. See the section on relative constructibility in constructible universeConstructible universe
In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
.
See also
- 0†Zero daggerIn set theory, 0† is a particular subset of the natural numbers, first defined by Robert M. Solovay in unpublished work in the 1960s. The definition is a bit awkward, because there might be no set of natural numbers satisfying the conditions...
, a set similar to 0# where the constructible universe is replaced by a larger inner model with a measurable cardinalMeasurable cardinal- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
.