
Ineffable cardinal
Encyclopedia
In the mathematics
of transfinite number
s, an ineffable cardinal is a certain kind of large cardinal number, introduced by .
A cardinal number
 is called almost ineffable if for every
is called almost ineffable if for every 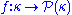 (where
(where 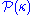 is the powerset of
is the powerset of  ) with the property that
) with the property that 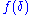 is a subset of
is a subset of 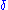 for all ordinals
for all ordinals  , there is a subset
, there is a subset 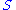 of
of  having cardinal
having cardinal  and homogeneous for
and homogeneous for 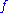 , in the sense that for any
, in the sense that for any  in
in 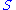 ,
, 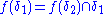 .
.
A cardinal number
 is called ineffable if for every binary-valued function
is called ineffable if for every binary-valued function 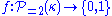 , there is a stationary subset of
, there is a stationary subset of  on which
on which 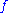 is homogeneous: that is, either
is homogeneous: that is, either 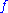 maps all unordered pairs of elements drawn from that subset to zero, or it maps all such unordered pairs to one.
maps all unordered pairs of elements drawn from that subset to zero, or it maps all such unordered pairs to one.
More generally, is called
is called  -ineffable (for a positive integer
-ineffable (for a positive integer  ) if for every
) if for every 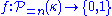 there is a stationary subset of
there is a stationary subset of  on which
on which 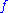 is
is  -homogeneous (takes the same value for all unordered
-homogeneous (takes the same value for all unordered  -tuples drawn from the subset). Thus, it is ineffable if and only if it is 2-ineffable.
-tuples drawn from the subset). Thus, it is ineffable if and only if it is 2-ineffable.
A totally ineffable cardinal is a cardinal that is -ineffable for every
-ineffable for every 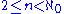 . If
. If  is
is 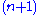 -ineffable, then the set of
-ineffable, then the set of  -ineffable cardinals below
-ineffable cardinals below  is a stationary subset of
is a stationary subset of  .
.
Totally ineffable cardinals are of greater consistency strength than subtle cardinal
s and of lesser consistency strength than remarkable cardinals. A list of large cardinal axioms by consistency strength is available here.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
of transfinite number
Transfinite number
Transfinite numbers are numbers that are "infinite" in the sense that they are larger than all finite numbers, yet not necessarily absolutely infinite. The term transfinite was coined by Georg Cantor, who wished to avoid some of the implications of the word infinite in connection with these...
s, an ineffable cardinal is a certain kind of large cardinal number, introduced by .
A cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
 is called almost ineffable if for every
is called almost ineffable if for every 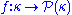 (where
(where 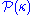 is the powerset of
is the powerset of  ) with the property that
) with the property that 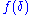 is a subset of
is a subset of 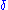 for all ordinals
for all ordinals  , there is a subset
, there is a subset 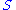 of
of  having cardinal
having cardinal  and homogeneous for
and homogeneous for 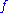 , in the sense that for any
, in the sense that for any  in
in 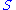 ,
, 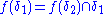 .
.A cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
 is called ineffable if for every binary-valued function
is called ineffable if for every binary-valued function 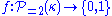 , there is a stationary subset of
, there is a stationary subset of  on which
on which 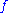 is homogeneous: that is, either
is homogeneous: that is, either 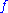 maps all unordered pairs of elements drawn from that subset to zero, or it maps all such unordered pairs to one.
maps all unordered pairs of elements drawn from that subset to zero, or it maps all such unordered pairs to one.More generally,
 is called
is called  -ineffable (for a positive integer
-ineffable (for a positive integer  ) if for every
) if for every 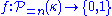 there is a stationary subset of
there is a stationary subset of  on which
on which 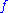 is
is  -homogeneous (takes the same value for all unordered
-homogeneous (takes the same value for all unordered  -tuples drawn from the subset). Thus, it is ineffable if and only if it is 2-ineffable.
-tuples drawn from the subset). Thus, it is ineffable if and only if it is 2-ineffable.A totally ineffable cardinal is a cardinal that is
 -ineffable for every
-ineffable for every 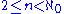 . If
. If  is
is 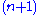 -ineffable, then the set of
-ineffable, then the set of  -ineffable cardinals below
-ineffable cardinals below  is a stationary subset of
is a stationary subset of  .
.Totally ineffable cardinals are of greater consistency strength than subtle cardinal
Subtle cardinal
In mathematics, subtle cardinals and ethereal cardinals are closely related kinds of large cardinal number.A cardinal κ is called subtle if for every closed and unbounded C ⊂ κ and for every sequence A of length κ for which element number δ , Aδ ⊂ δ there...
s and of lesser consistency strength than remarkable cardinals. A list of large cardinal axioms by consistency strength is available here.

