Group with operators
Encyclopedia
In abstract algebra
, a branch of pure mathematics
, the algebraic structure
group with operators or Ω-group is a group
with a set of group endomorphism
s.
Groups with operators were extensively studied by Emmy Noether
and her school in the 1920s. She employed the concept in her original formulation of the three Noether isomorphism theorems.
) is a group G together with a family of function
s
:
which are distributive with respect to the group operation.
is called the operator domain, and its elements are called the homotheties of G.
We denote the image of a group element g under a function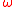
with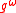 
. The distributivity can then be expressed as
A subgroup S of G is called a stable subgroup,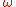
-subgroup or 
-invariant subgroup if it respects the homotheties, that is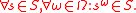
, a group with operators can be defined as an object of a functor category
GrpM where M is a monoid (i.e., a category with one object) and Grp denotes the category of groups
. This definition is equivalent to the previous one.
A group with operators is also a mapping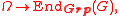
where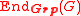
is the set of group endomorphism
s of G.
is analogous to that of compactness
in topology
, and can sometimes be too strong a requirement. It is natural to talk about "compactness relative to a set", i.e. talk about composition series
where each (normal) subgroup is an operator-subgroup relative to the operator set X, of the group in question.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a branch of pure mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
group with operators or Ω-group is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
with a set of group endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s.
Groups with operators were extensively studied by Emmy Noether
Emmy Noether
Amalie Emmy Noether was an influential German mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics. Described by David Hilbert, Albert Einstein and others as the most important woman in the history of mathematics, she revolutionized the theories of...
and her school in the 1920s. She employed the concept in her original formulation of the three Noether isomorphism theorems.
Definition
A group with operators (G,) is a group G together with a family of functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s
:which are distributive with respect to the group operation.
is called the operator domain, and its elements are called the homotheties of G.We denote the image of a group element g under a function
with 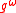. The distributivity can then be expressed asA subgroup S of G is called a stable subgroup,
-subgroup or -invariant subgroup if it respects the homotheties, that is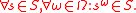Category-theoretic remarks
In category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a group with operators can be defined as an object of a functor category
Functor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
GrpM where M is a monoid (i.e., a category with one object) and Grp denotes the category of groups
Category of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
. This definition is equivalent to the previous one.
A group with operators is also a mapping
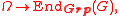
where
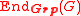is the set of group endomorphismEndomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s of G.
Examples
- Given any group G, (G, ∅) is trivially a group with operators
- Given an R-moduleModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
M, the group M operates on the operator domain R by scalar multiplicationScalar multiplicationIn mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
. More concretely, every vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
is a group with operators.
Applications
The Jordan–Hölder theorem also holds in the context of operator groups. The requirement that a group have a composition seriesComposition series
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
is analogous to that of compactness
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, and can sometimes be too strong a requirement. It is natural to talk about "compactness relative to a set", i.e. talk about composition series
Composition series
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
where each (normal) subgroup is an operator-subgroup relative to the operator set X, of the group in question.