Wilson's theorem
Encyclopedia
In mathematics
, Wilson's theorem states that a natural number n > 1 is a prime number
if and only if
(see factorial
and modular arithmetic
for the notation).
(a student of the English mathematician
Edward Waring
) who stated it in the 18th century. Waring announced the theorem in 1770, although neither he nor Wilson could prove it. Lagrange
gave the first proof in 1771. There is evidence that Leibniz
was also aware of the result a century earlier, but he never published it.
However if p is prime, then each of the above integers are relatively prime to p. It is easy to check the result when p is 2 or 3, so let us assume p > 3. So for each of these integers a there is another b such that ab ≡ 1 (mod p). It is important to note that this b is unique modulo p, and that since p is prime, a ≡ b if and only if a is 1 or p − 1. Now if we omit 1 and p − 1, then the others can be grouped into pairs whose product is 1 showing
2.3.4.….(p − 2) ≡ 1 (mod p)or more simply (p − 2)! ≡ 1 (mod p)). Finally, multiply this equality by p − 1 to complete the proof. For example, if p ≡ 11, we have
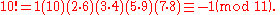
The commutative and associative properties are used in above procedure. All elements in the above product will be of the form g g −1 ≡ 1 (mod p) except 1 (p − 1) which is left.
If p = 2, the result is trivial to check.
To prove the converse (see below for a more exact converse result), suppose the congruence
holds for a composite
n, and note that then n has a proper divisor
d with 1 < d < n. Clearly, d divides (n − 1)! . But by the congruence, d also divides (n − 1)! + 1, so that d divides 1, a contradiction.
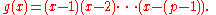
From Lagrange's theorem
, if f(x) is a nonzero polynomial of degree d over a field
F, then f(x) has at most d roots over F. Now, with g(x) as above, consider the polynomial
Since the leading coefficients cancel, we see that f(x) is a polynomial of degree at most p − 2. Reducing mod p, we see that f(x) has at most p − 2 roots mod p. But by Fermat's little theorem
, each of the elements 1, 2, ..., p − 1 is a root of f(x). This is impossible, unless f(x) is identically zero mod p, i.e. unless each coefficient of f(x) is divisible by p.
But since p is odd, the constant term of f(x) is just (p − 1)! + 1, and the result follows.
in practice, since computing (n − 1)! modulo n for large n is hard, and far easier primality tests are known (indeed, even trial division
is considerably more efficient).
Using Wilson's Theorem, for any odd prime p = 2m + 1 we can rearrange the left hand side of
to obtain the equality
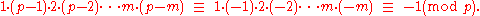
This becomes
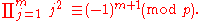
We can use this fact to prove part of a famous result: for any prime p such that p ≡ 1 (mod 4) the number (−1) is a square (quadratic residue) mod p. For suppose p = 4k + 1 for some integer k. Then we can take m = 2k above, and we conclude that
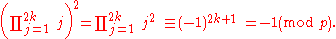
Wilson's theorem has been used to construct formulas for primes, but they are too slow to have practical value.
From the above proofs we already know that for prime
n we have (n − 1)! ≡ −1 (mod n).
We can easily verify the case n = 4 (note that n = 1 must be excluded because −1 ≡ 0 (mod n) creates ambiguity in the statement). Which leaves us with the case where n is a composite number
larger than 5. In this case the above statement claims that n divides (n − 1)! . We will now prove this.
Note that by definition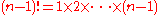
.
We will show that we can always find two of these n − 1 terms such that their product is divisible by n.
In most cases, a composite n > 5 has a divisor a such that 2 ≤ a < (n/a). In such case, the two terms are a and (n/a).
The only case when no such a exists is if n is a square
of a prime p > 2. In this case, the two terms are p and 2p.
:
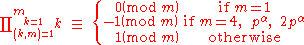
where p is an odd prime, and
is a positive integer. This further generalizes to the fact that in any finite abelian group, either the product of all elements is the identity, or there is precisely one element a of order 2. In the latter case, the product of all elements equals a.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Wilson's theorem states that a natural number n > 1 is a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
(see factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
and modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
for the notation).
History
The theorem was known to Ibn al-Haytham (also known as Alhazen) in circa 1000 AD, but it is named after John WilsonJohn Wilson (mathematician)
John Wilson was an English mathematician. The theorem, Wilson's Theorem, named after him for its discovery from Ibn al-Haytham, not its proof....
(a student of the English mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Edward Waring
Edward Waring
Edward Waring was an English mathematician who was born in Old Heath , Shropshire, England and died in Pontesbury, Shropshire, England. He entered Magdalene College, Cambridge as a sizar and became Senior wrangler in 1757. He was elected a Fellow of Magdalene and in 1760 Lucasian Professor of...
) who stated it in the 18th century. Waring announced the theorem in 1770, although neither he nor Wilson could prove it. Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
gave the first proof in 1771. There is evidence that Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
was also aware of the result a century earlier, but he never published it.
First proof
If p is composite, then its positive divisors are among the integers 1, 2, 3, 4, … , p − 1 and it is clear that gcd((p − 1)!, p) > 1, so we can not have (p − 1)! ≡ −1 (mod p).However if p is prime, then each of the above integers are relatively prime to p. It is easy to check the result when p is 2 or 3, so let us assume p > 3. So for each of these integers a there is another b such that ab ≡ 1 (mod p). It is important to note that this b is unique modulo p, and that since p is prime, a ≡ b if and only if a is 1 or p − 1. Now if we omit 1 and p − 1, then the others can be grouped into pairs whose product is 1 showing
2.3.4.….(p − 2) ≡ 1 (mod p)or more simply (p − 2)! ≡ 1 (mod p)). Finally, multiply this equality by p − 1 to complete the proof. For example, if p ≡ 11, we have
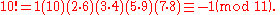
The commutative and associative properties are used in above procedure. All elements in the above product will be of the form g g −1 ≡ 1 (mod p) except 1 (p − 1) which is left.
If p = 2, the result is trivial to check.
To prove the converse (see below for a more exact converse result), suppose the congruence
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
holds for a composite
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
n, and note that then n has a proper divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
d with 1 < d < n. Clearly, d divides (n − 1)
Second proof
Here is another proof of the first direction: the result is clearly true for p = 2, so suppose p is a prime greater than 2 (and therefore odd). Consider the polynomial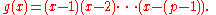From Lagrange's theorem
Lagrange's theorem (number theory)
In number theory, Lagrange's theorem states that:If the modulus is not prime, then it is possible for there to be more than n solutions. The exact number of solutions can be determined by finding the prime factorization of n...
, if f(x) is a nonzero polynomial of degree d over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F, then f(x) has at most d roots over F. Now, with g(x) as above, consider the polynomial
Since the leading coefficients cancel, we see that f(x) is a polynomial of degree at most p − 2. Reducing mod p, we see that f(x) has at most p − 2 roots mod p. But by Fermat's little theorem
Fermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
, each of the elements 1, 2, ..., p − 1 is a root of f(x). This is impossible, unless f(x) is identically zero mod p, i.e. unless each coefficient of f(x) is divisible by p.
But since p is odd, the constant term of f(x) is just (p − 1)! + 1, and the result follows.
Applications
Wilson's theorem is useless as a primality testPrimality test
A primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
in practice, since computing (n − 1)! modulo n for large n is hard, and far easier primality tests are known (indeed, even trial division
Trial division
Trial division is the most laborious but easiest to understand of the integer factorization algorithms. Its ease of implementation makes it a viable integer factorization option for devices with little available memory, such as graphing calculators....
is considerably more efficient).
Using Wilson's Theorem, for any odd prime p = 2m + 1 we can rearrange the left hand side of
to obtain the equality
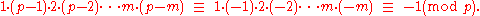
This becomes
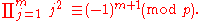
We can use this fact to prove part of a famous result: for any prime p such that p ≡ 1 (mod 4) the number (−1) is a square (quadratic residue) mod p. For suppose p = 4k + 1 for some integer k. Then we can take m = 2k above, and we conclude that
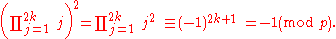
Wilson's theorem has been used to construct formulas for primes, but they are too slow to have practical value.
A simple generalization
Wilson's theorem can be generalized to the following statement:From the above proofs we already know that for prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
n we have (n − 1)! ≡ −1 (mod n).
We can easily verify the case n = 4 (note that n = 1 must be excluded because −1 ≡ 0 (mod n) creates ambiguity in the statement). Which leaves us with the case where n is a composite number
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
larger than 5. In this case the above statement claims that n divides (n − 1)
Note that by definition
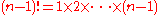.We will show that we can always find two of these n − 1 terms such that their product is divisible by n.
In most cases, a composite n > 5 has a divisor a such that 2 ≤ a < (n/a). In such case, the two terms are a and (n/a).
The only case when no such a exists is if n is a square
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
of a prime p > 2. In this case, the two terms are p and 2p.
Gauss's generalization
The following is a stronger generalization of Wilson's theorem, due to Carl Friedrich GaussCarl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
:
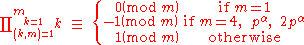
where p is an odd prime, and
is a positive integer. This further generalizes to the fact that in any finite abelian group, either the product of all elements is the identity, or there is precisely one element a of order 2. In the latter case, the product of all elements equals a.