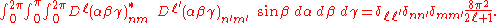Schur orthogonality relations
Encyclopedia
In mathematics, the Schur orthogonality relations express a central fact about representations
of finite groups
.
They admit a generalization to the case of compact group
s in general, and in particular compact Lie groups
, such as the
rotation group
SO(3).
s of a finite group G has a natural inner product
:

where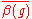 means the complex conjugate of the value of
means the complex conjugate of the value of  on g. With respect to this inner product, the irreducible characters
on g. With respect to this inner product, the irreducible characters
form an orthonormal basis
for the space of class functions, and this yields the orthogonality relation for the rows of the character
table:

For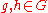 the orthogonality relation for columns is as follows:
the orthogonality relation for columns is as follows:
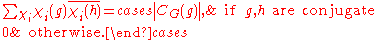
where the sum is over all of the irreducible characters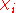 of G and the symbol
of G and the symbol 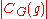 denotes the order of the centralizer of
denotes the order of the centralizer of 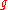 .
.
The orthogonality relations can aid many computations including:
 be a matrix
be a matrix
element of an irreducible matrix representation
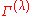 of a finite group
of a finite group  of order |G|, i.e., G has |G| elements. Since it can be proven that any matrix representation of any finite group is equivalent to a unitary representation
of order |G|, i.e., G has |G| elements. Since it can be proven that any matrix representation of any finite group is equivalent to a unitary representation
, we assume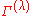 is unitary:
is unitary: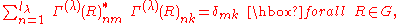
where is the (finite) dimension of the irreducible representation
is the (finite) dimension of the irreducible representation 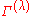 .
.
The orthogonality relations, only valid for matrix elements of irreducible representations, are:

Here is the complex conjugate of
is the complex conjugate of  and the sum is over all elements of G.
and the sum is over all elements of G.
The Kronecker delta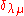 is unity if the matrices are in the same irreducible representation
is unity if the matrices are in the same irreducible representation  . If
. If 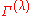 and
and 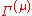 are non-equivalent
are non-equivalent
it is zero. The other two Kronecker delta's state that
the row and column indices must be equal (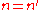 and
and  ) in order to obtain a non-vanishing result. This theorem is also known as the Great (or Grand) Orthogonality Theorem.
) in order to obtain a non-vanishing result. This theorem is also known as the Great (or Grand) Orthogonality Theorem.
Every group has an identity representation (all group elements mapped onto the real number 1).
This is an irreducible representation. The great orthogonality relations immediately imply that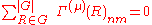
for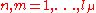 and any irreducible representation
and any irreducible representation 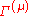 not equal to the identity representation.
not equal to the identity representation.
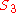 (symmetric group
(symmetric group
). This group is isomorphic to the point group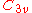 , consisting of a threefold rotation axis and three vertical mirror planes. The groups have a 2-dimensional irreducible representation (l = 2). In the case of
, consisting of a threefold rotation axis and three vertical mirror planes. The groups have a 2-dimensional irreducible representation (l = 2). In the case of 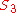 one usually labels this representation
one usually labels this representation
by the Young tableau
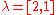 and in the case of
and in the case of 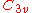
one usually writes . In both cases the representation consists of the following six real matrices, each representing a single group element:
. In both cases the representation consists of the following six real matrices, each representing a single group element: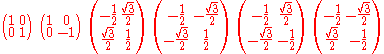
The normalization of the (1,1) element: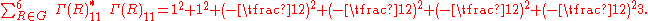
In the same manner one can show the normalization of the other matrix elements: (2,2), (1,2), and (2,1).
The orthogonality of the (1,1) and (2,2) elements: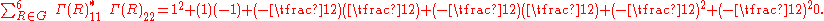
Similar relations hold for the orthogonality of the elements (1,1) and (1,2), etc.
One verifies easily in the example that all sums of corresponding matrix elements vanish because of
the orthogonality of the given irreducible representation to the identity representation.
of a matrix is a sum of diagonal matrix elements,
 .
.
The collection of traces is the character of a representation. Often one writes for
of a representation. Often one writes for
the trace of a matrix in an irreducible representation with character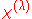
 .
.
In this notation we can write several character formulas:
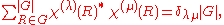
which allows us to check whether or not a representation is irreducible. (The formula means that the lines in any character table have to be orthogonal vectors.)
And
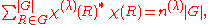
which helps us to determine how often the irreducible representation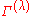 is contained within the reducible representation
is contained within the reducible representation  with character
with character 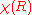 .
.
For instance, if

and the order of the group is
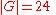
then the number of times that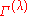 is contained within the given
is contained within the given
reducible representation is
is
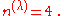
See Character theory
for more about group characters.
Every compact group has unique bi-invariant Haar measure
has unique bi-invariant Haar measure
, so that the volume of the group is 1. Denote this measure by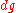 . Let
. Let 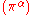 be a complete set of irreducible representations of
be a complete set of irreducible representations of  , and let
, and let 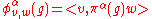 be a matrix coefficient
be a matrix coefficient
of the representation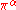 . The orthogonality relations can the be stated in two parts:
. The orthogonality relations can the be stated in two parts:
1) If then
then
2) If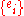 is an orthonormal basis
is an orthonormal basis
of the representation space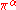 then
then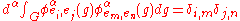
where is the dimension of
is the dimension of 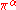 . These orthogonality relations and the fact that all of the representations have finite dimensions are consequences of the Peter-Weyl theorem
. These orthogonality relations and the fact that all of the representations have finite dimensions are consequences of the Peter-Weyl theorem
An Example
An example of an r = 3 parameter group is the matrix group SO(3) consisting of all 3 x 3 orthogonal matrices with unit determinant. A possible parametrization of this group is in terms of Euler angles: 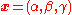 (see e.g., this article for the explicit from of an element of SO(3) in terms of Euler angles). The bounds are
(see e.g., this article for the explicit from of an element of SO(3) in terms of Euler angles). The bounds are  and
and  .
.
Not only the recipe for the computation of the volume element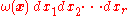 depends on the chosen parameters, but also the final result, i.e., the analytic form of the weight function (measure)
depends on the chosen parameters, but also the final result, i.e., the analytic form of the weight function (measure) 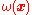 .
.
For instance, the Euler angle parametrization of SO(3) gives the weight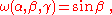 while the n, ψ parametrization gives the weight
while the n, ψ parametrization gives the weight 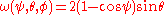
with
It can be shown that the irreducible matrix representations of compact Lie groups are finite-dimensional and can be chosen to be unitary:
With the short-hand notation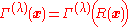
the orthogonality relations take the form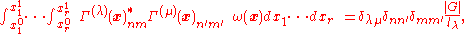
with the volume of the group:
As an example we note that the irreducible representations of SO(3) are Wigner D-matrices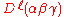 , which are of dimension
, which are of dimension  . Since
. Since
they satisfy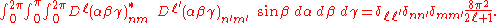
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of finite groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
They admit a generalization to the case of compact group
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
s in general, and in particular compact Lie groups
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
, such as the
rotation group
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
SO(3).
Intrinsic statement
The space of complex-valued class functionClass function
In mathematics, especially in the fields of group theory and representation theory of groups, a class function is a function f on a group G, such that f is constant on the conjugacy classes of G. In other words, f is invariant under the conjugation map on G...
s of a finite group G has a natural inner product
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
:

where
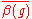 means the complex conjugate of the value of
means the complex conjugate of the value of  on g. With respect to this inner product, the irreducible characters
on g. With respect to this inner product, the irreducible charactersCharacter theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
form an orthonormal basis
for the space of class functions, and this yields the orthogonality relation for the rows of the character
table:

For
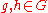 the orthogonality relation for columns is as follows:
the orthogonality relation for columns is as follows:
where the sum is over all of the irreducible characters
 of G and the symbol
of G and the symbol  denotes the order of the centralizer of
denotes the order of the centralizer of 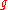 .
.The orthogonality relations can aid many computations including:
- decomposing an unknown character as a linear combination of irreducible characters;
- constructing the complete character table when only some of the irreducible characters are known;
- finding the orders of the centralizers of representatives of the conjugacy classes of a group; and
- finding the order of the group.
Coordinates statement
Let be a matrix
be a matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
element of an irreducible matrix representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
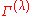 of a finite group
of a finite group  of order |G|, i.e., G has |G| elements. Since it can be proven that any matrix representation of any finite group is equivalent to a unitary representation
of order |G|, i.e., G has |G| elements. Since it can be proven that any matrix representation of any finite group is equivalent to a unitary representationUnitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
, we assume
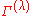 is unitary:
is unitary: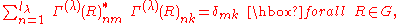
where
 is the (finite) dimension of the irreducible representation
is the (finite) dimension of the irreducible representation 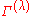 .
.The orthogonality relations, only valid for matrix elements of irreducible representations, are:

Here
 is the complex conjugate of
is the complex conjugate of  and the sum is over all elements of G.
and the sum is over all elements of G.The Kronecker delta
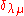 is unity if the matrices are in the same irreducible representation
is unity if the matrices are in the same irreducible representation  . If
. If 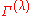 and
and 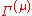 are non-equivalent
are non-equivalentit is zero. The other two Kronecker delta's state that
the row and column indices must be equal (
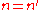 and
and  ) in order to obtain a non-vanishing result. This theorem is also known as the Great (or Grand) Orthogonality Theorem.
) in order to obtain a non-vanishing result. This theorem is also known as the Great (or Grand) Orthogonality Theorem.Every group has an identity representation (all group elements mapped onto the real number 1).
This is an irreducible representation. The great orthogonality relations immediately imply that
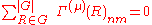
for
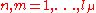 and any irreducible representation
and any irreducible representation 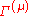 not equal to the identity representation.
not equal to the identity representation.Example of the permutation group on 3 objects
The 3! permutations of three objects form a group of order 6, commonly denoted by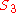 (symmetric group
(symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
). This group is isomorphic to the point group
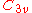 , consisting of a threefold rotation axis and three vertical mirror planes. The groups have a 2-dimensional irreducible representation (l = 2). In the case of
, consisting of a threefold rotation axis and three vertical mirror planes. The groups have a 2-dimensional irreducible representation (l = 2). In the case of 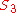 one usually labels this representation
one usually labels this representationby the Young tableau
Young tableau
In mathematics, a Young tableau is a combinatorial object useful in representation theory. It provides a convenient way to describe the group representations of the symmetric and general linear groups and to study their properties. Young tableaux were introduced by Alfred Young, a mathematician at...
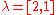 and in the case of
and in the case of 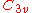
one usually writes
 . In both cases the representation consists of the following six real matrices, each representing a single group element:
. In both cases the representation consists of the following six real matrices, each representing a single group element: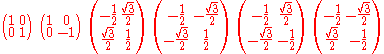
The normalization of the (1,1) element:
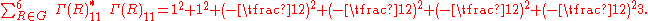
In the same manner one can show the normalization of the other matrix elements: (2,2), (1,2), and (2,1).
The orthogonality of the (1,1) and (2,2) elements:
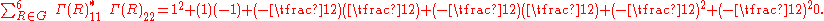
Similar relations hold for the orthogonality of the elements (1,1) and (1,2), etc.
One verifies easily in the example that all sums of corresponding matrix elements vanish because of
the orthogonality of the given irreducible representation to the identity representation.
Direct implications
The traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of a matrix is a sum of diagonal matrix elements,
 .
.The collection of traces is the character
 of a representation. Often one writes for
of a representation. Often one writes forthe trace of a matrix in an irreducible representation with character
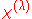
 .
.In this notation we can write several character formulas:
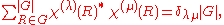
which allows us to check whether or not a representation is irreducible. (The formula means that the lines in any character table have to be orthogonal vectors.)
And
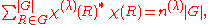
which helps us to determine how often the irreducible representation
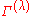 is contained within the reducible representation
is contained within the reducible representation  with character
with character 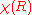 .
.For instance, if

and the order of the group is
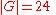
then the number of times that
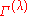 is contained within the given
is contained within the givenreducible representation
 is
is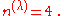
See Character theory
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
for more about group characters.
Compact Groups
The generalization of the orthogonality relations from finite groups to compact groups (which include compact Lie groups such as SO(3) )is basically simple: Replace the summation over the group by an integration over the group..Every compact group
 has unique bi-invariant Haar measure
has unique bi-invariant Haar measureHaar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
, so that the volume of the group is 1. Denote this measure by
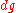 . Let
. Let 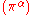 be a complete set of irreducible representations of
be a complete set of irreducible representations of  , and let
, and let 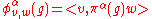 be a matrix coefficient
be a matrix coefficientMatrix coefficient
In mathematics, a matrix coefficient is a function on agroup of a special form, which depends on a linear representation of the group and additional data...
of the representation
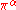 . The orthogonality relations can the be stated in two parts:
. The orthogonality relations can the be stated in two parts:1) If
 then
then
2) If
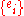 is an orthonormal basis
is an orthonormal basisOrthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of the representation space
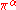 then
then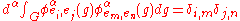
where
 is the dimension of
is the dimension of 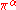 . These orthogonality relations and the fact that all of the representations have finite dimensions are consequences of the Peter-Weyl theorem
. These orthogonality relations and the fact that all of the representations have finite dimensions are consequences of the Peter-Weyl theoremAn Example 
An example of an r = 3 parameter group is the matrix group SO(3) consisting of all 3 x 3 orthogonal matrices with unit determinant. A possible parametrization of this group is in terms of Euler angles: 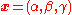 (see e.g., this article for the explicit from of an element of SO(3) in terms of Euler angles). The bounds are
(see e.g., this article for the explicit from of an element of SO(3) in terms of Euler angles). The bounds are  and
and  .
.Not only the recipe for the computation of the volume element
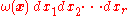 depends on the chosen parameters, but also the final result, i.e., the analytic form of the weight function (measure)
depends on the chosen parameters, but also the final result, i.e., the analytic form of the weight function (measure) 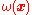 .
.For instance, the Euler angle parametrization of SO(3) gives the weight
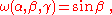 while the n, ψ parametrization gives the weight
while the n, ψ parametrization gives the weight 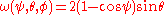
with

It can be shown that the irreducible matrix representations of compact Lie groups are finite-dimensional and can be chosen to be unitary:

With the short-hand notation
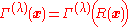
the orthogonality relations take the form
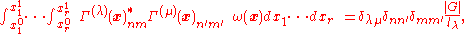
with the volume of the group:

As an example we note that the irreducible representations of SO(3) are Wigner D-matrices
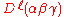 , which are of dimension
, which are of dimension  . Since
. Since
they satisfy