Quaternion algebra
Encyclopedia
In mathematics
, a quaternion algebra over a field F is a central simple algebra
A over F that has dimension 4 over F. Every quaternion algebra becomes the matrix algebra by extending scalars (=tensoring
with a field extension), i.e. for a suitable field extension
K of F,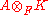
is isomorphic to the 2×2 matrix algebra
over K.
The notion of a quaternion algebra can be seen as a generalization of the Hamilton quaternions to an arbitrary base field. The Hamilton quaternions are a quaternion algebra (in the above sense) over
(the real number field), and indeed the only one over R apart from the 2×2 real matrix algebra, up to isomorphism.
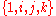, with the following multiplication rules:
where a and b are any given nonzero elements of F. A short calculation shows k2 = −ab. (The Hamilton quaternions are the case where
and a = b = −1.) When F has characteristic 2, a different explicit description in terms of a basis of 4 elements is also possible, but in any event the definition of a quaternion algebra over F as a 4-dimensional central simple algebra over F applies uniformly in all characteristics.
, particularly to quadratic form
s. They are concrete structures that generate the elements of order two in the Brauer group
of F. (For some fields, including algebraic number fields, every element of index 2 in its Brauer group is represented by a quaternion algebra. A theorem of Merkurjev says the elements of index 2 in the Brauer group of any field are represented by a tensor product of quaternion algebras.) In particular, over p-adic fields the construction of quaternion algebras can be viewed as the quadratic Hilbert symbol
of local class field theory.
that there are only two real quaternion algebras: 2×2 matrices over the reals and Hamilton's real quaternions.
In a similar way, over any local field
F there are exactly two quaternion algebras: the 2×2 matrices over F and a division algebra.
But the quaternion division algebra over a local field is usually not Hamilton's quaternions over the field. For example, over the p-adic numbers Hamilton's quaternions are a division algebra only when p is 2. For odd prime p, the p-adic Hamilton quaternions are isomorphic to the 2×2 matrices over the p-adics. To see the p-adic Hamilton quaternions are not a division algebra for odd prime p, observe that the congruence x2 + y2 = −1 mod p is solvable and therefore by Hensel's lemma
— here is where p being odd is needed — the equation
is solvable in the p-adic numbers. Therefore the quaternion
has norm 0 and hence doesn't have a multiplicative inverse.
One would like to classify the F-algebra isomorphism
classes of all quaternion algebras for a given field, F. One way to do this is to use the one-to-one correspondence between isomorphism classes of quaternion algebras over F and isomorphism classes of their norm forms.
To every quaternion algebra A, one can associate a quadratic form N (called the norm form
) on A such that
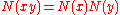
for all x and y in A. It turns out that the possible norm forms for quaternion F-algebras are exactly the Pfister 2-forms
.
.
Let
be a quaternion algebra over 
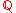and let 
be a place of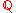 
, with completion 
(so it is either the p-adic numbers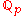
for some prime p or the real numbers 
). Define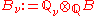 
, which is a quaternion algebra over 
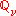. So there are two choices for
: the 2 by 2 matrices over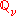 
or a division algebra.
We say that
is split (or unramified) at 
if 
is isomorphic to the 2×2 matrices over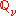 
. We say that B is non-split (or ramified) at 
if 
is the quaternion division algebra over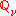 
. For example, the rational Hamilton quaternions is non-split at 2 and at 
and split at all odd primes. The rational 2 by 2 matrices are split at all places.
A quaternion algebra over the rationals which splits at
is analogous to a real quadratic field and one which is non-split at 
is analogous to an imaginary quadratic field. The analogy comes from a quadratic field having real embeddings when the minimal polynomial for a generator splits over the reals and having non-real embeddings otherwise. One illustration of the strength of this analogy concerns unit groups in an order of a rational quaternion algebra:
it is infinite if the quaternion algebra splits at
and it is finite otherwise, just as the unit group of an order in a quadratic ring is infinite in the real quadratic case and finite otherwise.
The number of places where a quaternion algebra over the rationals ramifies is always even, and this is equivalent to the quadratic reciprocity law over the rationals.
Moreover, the places where B ramifies determines B up to isomorphism as an algebra. (In other words, non-isomorphic quaternion algebras over the rationals do not share the same set of ramified places.) The product of the primes at which B ramifies is called the discriminant of B.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a quaternion algebra over a field F is a central simple algebra
Central simple algebra
In ring theory and related areas of mathematics a central simple algebra over a field K is a finite-dimensional associative algebra A, which is simple, and for which the center is exactly K...
A over F that has dimension 4 over F. Every quaternion algebra becomes the matrix algebra by extending scalars (=tensoring
Tensor product of algebras
In mathematics, the tensor product of two R-algebras is also an R-algebra. This gives us a tensor product of algebras. The special case R = Z gives us a tensor product of rings, since rings may be regarded as Z-algebras....
with a field extension), i.e. for a suitable field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
K of F,
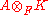is isomorphic to the 2×2 matrix algebraMatrix algebra
Matrix algebra may refer to:*Matrix theory, is the branch of mathematics that studies matrices*Matrix ring, thought of as an algebra over a field or a commutative ring...
over K.
The notion of a quaternion algebra can be seen as a generalization of the Hamilton quaternions to an arbitrary base field. The Hamilton quaternions are a quaternion algebra (in the above sense) over
(the real number field), and indeed the only one over R apart from the 2×2 real matrix algebra, up to isomorphism.Structure
Quaternion algebra here means something more general than the algebra of Hamilton quaternions. When the coefficient field F does not have characteristic 2, every quaternion algebra over F can be described as a 4-dimensional F-vector space with basis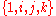, with the following multiplication rules:- i2 = a
- j2 = b
- ij = k
- ji = −k
where a and b are any given nonzero elements of F. A short calculation shows k2 = −ab. (The Hamilton quaternions are the case where
and a = b = −1.) When F has characteristic 2, a different explicit description in terms of a basis of 4 elements is also possible, but in any event the definition of a quaternion algebra over F as a 4-dimensional central simple algebra over F applies uniformly in all characteristics.Application
Quaternion algebras are applied in number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, particularly to quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s. They are concrete structures that generate the elements of order two in the Brauer group
Brauer group
In mathematics, the Brauer group of a field K is an abelian group whose elements are Morita equivalence classes of central simple algebras of finite rank over K and addition is induced by the tensor product of algebras. It arose out of attempts to classify division algebras over a field and is...
of F. (For some fields, including algebraic number fields, every element of index 2 in its Brauer group is represented by a quaternion algebra. A theorem of Merkurjev says the elements of index 2 in the Brauer group of any field are represented by a tensor product of quaternion algebras.) In particular, over p-adic fields the construction of quaternion algebras can be viewed as the quadratic Hilbert symbol
Hilbert symbol
In mathematics, given a local field K, such as the fields of reals or p-adic numbers, whose multiplicative group of non-zero elements is K×, the Hilbert symbol is an algebraic construction, extracted from reciprocity laws, and important in the formulation of local class field theory...
of local class field theory.
Classification
It is a theorem of FrobeniusFerdinand Georg Frobenius
Ferdinand Georg Frobenius was a German mathematician, best known for his contributions to the theory of differential equations and to group theory...
that there are only two real quaternion algebras: 2×2 matrices over the reals and Hamilton's real quaternions.
In a similar way, over any local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
F there are exactly two quaternion algebras: the 2×2 matrices over F and a division algebra.
But the quaternion division algebra over a local field is usually not Hamilton's quaternions over the field. For example, over the p-adic numbers Hamilton's quaternions are a division algebra only when p is 2. For odd prime p, the p-adic Hamilton quaternions are isomorphic to the 2×2 matrices over the p-adics. To see the p-adic Hamilton quaternions are not a division algebra for odd prime p, observe that the congruence x2 + y2 = −1 mod p is solvable and therefore by Hensel's lemma
Hensel's lemma
In mathematics, Hensel's lemma, also known as Hensel's lifting lemma, named after Kurt Hensel, is a result in modular arithmetic, stating that if a polynomial equation has a simple root modulo a prime number , then this root corresponds to a unique root of the same equation modulo any higher power...
— here is where p being odd is needed — the equation
- x2 + y2 = −1
is solvable in the p-adic numbers. Therefore the quaternion
- xi + yj + k
has norm 0 and hence doesn't have a multiplicative inverse.
One would like to classify the F-algebra isomorphism
Algebra homomorphism
A homomorphism between two algebras, A and B, over a field K, is a map F:A\rightarrow B such that for all k in K and x,y in A,* F = kF* F = F + F...
classes of all quaternion algebras for a given field, F. One way to do this is to use the one-to-one correspondence between isomorphism classes of quaternion algebras over F and isomorphism classes of their norm forms.
To every quaternion algebra A, one can associate a quadratic form N (called the norm form
Norm form
In mathematics, a norm form is a homogeneous form in n variables constructed from the field norm of a field extension L/K of degree n...
) on A such that
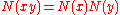
for all x and y in A. It turns out that the possible norm forms for quaternion F-algebras are exactly the Pfister 2-forms
Pfister form
In mathematics, a Pfister form is a particular kind of quadratic form over a field F , introduced by A. Pfister in 1965. A Pfister form is in 2n variables, for some natural number n , and may be written as a tensor product of quadratic forms as:\langle \langle a_1, a_2, .....
.
Quaternion algebras over the rational numbers
Quaternion algebras over the rational numbers have an arithmetic theory similar to, but more complicated than, that of quadratic extensions of.Let
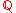be a quaternion algebra over and let be a place of 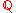, with completion (so it is either the p-adic numbers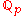 for some prime p or the real numbers ). Define 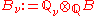, which is a quaternion algebra over 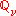. So there are two choices for: the 2 by 2 matrices over 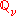or a division algebra.We say that
is split (or unramified) at if is isomorphic to the 2×2 matrices over 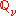. We say that B is non-split (or ramified) at if is the quaternion division algebra over 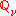. For example, the rational Hamilton quaternions is non-split at 2 and at and split at all odd primes. The rational 2 by 2 matrices are split at all places.A quaternion algebra over the rationals which splits at
is analogous to a real quadratic field and one which is non-split at is analogous to an imaginary quadratic field. The analogy comes from a quadratic field having real embeddings when the minimal polynomial for a generator splits over the reals and having non-real embeddings otherwise. One illustration of the strength of this analogy concerns unit groups in an order of a rational quaternion algebra:it is infinite if the quaternion algebra splits at
and it is finite otherwise, just as the unit group of an order in a quadratic ring is infinite in the real quadratic case and finite otherwise.The number of places where a quaternion algebra over the rationals ramifies is always even, and this is equivalent to the quadratic reciprocity law over the rationals.
Moreover, the places where B ramifies determines B up to isomorphism as an algebra. (In other words, non-isomorphic quaternion algebras over the rationals do not share the same set of ramified places.) The product of the primes at which B ramifies is called the discriminant of B.
See also
- composition algebraComposition algebraIn mathematics, a composition algebra A over a field K is a unital algebra over K together with a nondegenerate quadratic form N which satisfiesN = NN\,...
- cyclic algebra
- octonion algebraOctonion algebraIn mathematics, an octonion algebra over a field F is an algebraic structure which is an 8-dimensional composition algebra over F. In other words, it is a unital nonassociative algebra A over F with a nondegenerate quadratic form N such thatN = NNfor all x and y in A.The most well-known example of...
- Hurwitz quaternion orderHurwitz quaternion orderThe Hurwitz quaternion order is a specific order in a quaternion algebra over a suitable number field. The order is of particular importance in Riemann surface theory, in connection with surfaces with maximal symmetry, namely the Hurwitz surfaces. The Hurwitz quaternion order was studied in 1967...
- Hurwitz quaternionHurwitz quaternionIn mathematics, a Hurwitz quaternion is a quaternion whose components are either all integers or all half-integers...