
Vlasov equation
Encyclopedia
The Vlasov equation is a differential equation describing time evolution of the distribution function of plasma
consisting of charged particles with long-range (for example, Coulomb
) interaction. The equation was first suggested for description of plasma by Anatoly Vlasov
in 1938 (see also ) and later discussed by him in detail in a monograph.
approach based on the Boltzmann equation
has difficulties when applied to a description of the plasma with long-range Coulomb interaction
. He mentions the following problems arising when applying the kinetic theory based on pair collisions to plasma dynamics:
Vlasov
suggests that these difficulties originate from the long-range character of Coulomb interaction.
He starts with the collisionless Boltzmann equation (sometimes anachronistically called the Vlasov equation in this context),
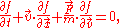
and adapted it to the case of a plasma, leading to the systems of equations shown below.
s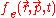 and
and 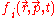 for electron
for electron
s and (positive) plasma ion
s. The distribution function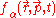 for species
for species  describes the number of particles of the species
describes the number of particles of the species  having approximately the momentum
having approximately the momentum
 near the position
near the position 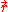 at time
at time  . Instead of the Boltzmann equation, the following system of equations was proposed for description of charged components of plasma (electrons and positive ions):
. Instead of the Boltzmann equation, the following system of equations was proposed for description of charged components of plasma (electrons and positive ions):
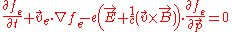
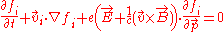

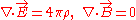
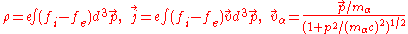
Here is the electron charge,
is the electron charge,  is the speed of light
is the speed of light
, the mass of the electron and ion respectively,
the mass of the electron and ion respectively, 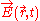 and
and 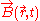 represent collective self-consistent electromagnetic field created in the point
represent collective self-consistent electromagnetic field created in the point  at time moment
at time moment  by all plasma particles. The essential difference of this system of equations from equations for particles in an external electromagnetic field is that the self-consistent electromagnetic field depends in a complex way on the distribution functions of electrons and ions
by all plasma particles. The essential difference of this system of equations from equations for particles in an external electromagnetic field is that the self-consistent electromagnetic field depends in a complex way on the distribution functions of electrons and ions 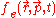 and
and 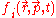 .
.
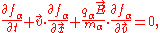
and Poisson’s equation for self-consistent electric field (in CGS units):

Here is the particle’s electric charge,
is the particle’s electric charge,  is the particle’s mass,
is the particle’s mass, 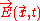 is the self-consistent electric field
is the self-consistent electric field
,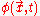 the self-consistent electric potential
the self-consistent electric potential
and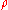 is the electric charge
is the electric charge
density.
Vlasov–Poisson equations are used to describe various phenomena in plasma, in particular Landau damping
and the distributions in a double layer
plasma, where they are necessarily strongly non-, and therefore inaccessible to fluid models.
and magnetohydrodynamics
(MHD))
one does not consider the velocity
distribution. This is achieved by replacing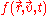 with plasma moments such as number density,
with plasma moments such as number density,  , mean velocity,
, mean velocity,  and pressure,
and pressure, 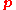
. They are named plasma moments because the nth
moment of can be found by integrating
can be found by integrating 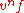 over velocity.
over velocity.
These variables are only functions of position and time, which means
that some information is lost. In multifluid theory, the different particle
species are treated as different fluids with different pressures,
densities and flow velocities. The equations governing the plasma moments are called the moment or fluid equations.
Below the two most used moment equations are presented (in SI units). Deriving the moment equations from
the Vlasov equation requires no assumptions about the distribution function.
It can be found by integration of the Vlasov equation over the entire
velocity space.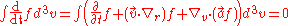
After some calculations, one ends up with .
.
The particle density , and the average velocity
, and the average velocity  , are zeroth and first order moments:
, are zeroth and first order moments: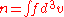
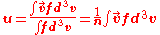
equation: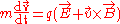
By using this equation and the Vlasov Equation, the momentum equation for each fluid
becomes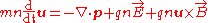 ,
,
where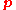 is the pressure tensor. The total time derivative
is the pressure tensor. The total time derivative
is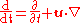 .
.
The pressure tensor is defined as the mass density times the covariance matrix
of the velocity:
Plasma (physics)
In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas may ionize its molecules or atoms , thus turning it into a plasma, which contains charged particles: positive ions and negative electrons or ions...
consisting of charged particles with long-range (for example, Coulomb
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
) interaction. The equation was first suggested for description of plasma by Anatoly Vlasov
Anatoly Vlasov
Anatoly Alexandrovich Vlasov was a Russian theoretical physicist prominent in the fields of statistical mechanics, kinetics, and especially in plasma physics.-Biography:...
in 1938 (see also ) and later discussed by him in detail in a monograph.
Difficulties of the standard kinetic approach
First, Vlasov argues that the standard kineticKinetic theory
The kinetic theory of gases describes a gas as a large number of small particles , all of which are in constant, random motion. The rapidly moving particles constantly collide with each other and with the walls of the container...
approach based on the Boltzmann equation
Boltzmann equation
The Boltzmann equation, also often known as the Boltzmann transport equation, devised by Ludwig Boltzmann, describes the statistical distribution of one particle in rarefied gas...
has difficulties when applied to a description of the plasma with long-range Coulomb interaction
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
. He mentions the following problems arising when applying the kinetic theory based on pair collisions to plasma dynamics:
- Theory of pair collisions disagree with the discovery by RayleighJohn Strutt, 3rd Baron RayleighJohn William Strutt, 3rd Baron Rayleigh, OM was an English physicist who, with William Ramsay, discovered the element argon, an achievement for which he earned the Nobel Prize for Physics in 1904...
, Irving LangmuirIrving LangmuirIrving Langmuir was an American chemist and physicist. His most noted publication was the famous 1919 article "The Arrangement of Electrons in Atoms and Molecules" in which, building on Gilbert N. Lewis's cubical atom theory and Walther Kossel's chemical bonding theory, he outlined his...
and Lewi TonksLewi TonksLewi Tonks was an American quantum physicist noted for his discovery of the Tonks-Girardeau gas.Tonks was employed by the General Electric for most of his working life, researching microwaves and ferromagnetism...
of natural vibrations in electron plasma. - Theory of pair collisions formally not applicable to Coulomb interaction due to the divergence of the kinetic terms.
- Theory of pair collisions can not explain experiments by Harrison Merrill and Harold Webb on anomalous electron scattering in gaseous plasma.
Vlasov
Anatoly Vlasov
Anatoly Alexandrovich Vlasov was a Russian theoretical physicist prominent in the fields of statistical mechanics, kinetics, and especially in plasma physics.-Biography:...
suggests that these difficulties originate from the long-range character of Coulomb interaction.
He starts with the collisionless Boltzmann equation (sometimes anachronistically called the Vlasov equation in this context),
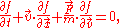
and adapted it to the case of a plasma, leading to the systems of equations shown below.
The Vlasov–Maxwell system of equations (cgs units)
Then, instead of collision-based kinetic description for interaction of charged particles in plasma, Vlasov suggests to use a self-consistent collective field created by charged plasma particles. Such description uses distribution functionDistribution function
In molecular kinetic theory in physics, a particle's distribution function is a function of seven variables, f, which gives the number of particles per unit volume in phase space. It is the number of particles per unit volume having approximately the velocity near the place and time...
s
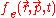 and
and 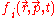 for electron
for electronElectron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s and (positive) plasma ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
s. The distribution function
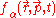 for species
for species  describes the number of particles of the species
describes the number of particles of the species  having approximately the momentum
having approximately the momentumMomentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
 near the position
near the position 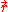 at time
at time  . Instead of the Boltzmann equation, the following system of equations was proposed for description of charged components of plasma (electrons and positive ions):
. Instead of the Boltzmann equation, the following system of equations was proposed for description of charged components of plasma (electrons and positive ions):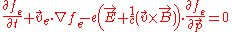
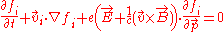

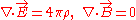
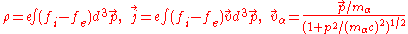
Here
 is the electron charge,
is the electron charge,  is the speed of light
is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
,
 the mass of the electron and ion respectively,
the mass of the electron and ion respectively, 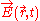 and
and 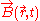 represent collective self-consistent electromagnetic field created in the point
represent collective self-consistent electromagnetic field created in the point 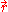 at time moment
at time moment  by all plasma particles. The essential difference of this system of equations from equations for particles in an external electromagnetic field is that the self-consistent electromagnetic field depends in a complex way on the distribution functions of electrons and ions
by all plasma particles. The essential difference of this system of equations from equations for particles in an external electromagnetic field is that the self-consistent electromagnetic field depends in a complex way on the distribution functions of electrons and ions 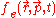 and
and 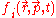 .
.The Vlasov–Poisson equation
The Vlasov–Poisson equations are an approximation of the Vlasov–Maxwell equations in the nonrelativistic zero-magnetic field limit: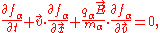
and Poisson’s equation for self-consistent electric field (in CGS units):

Here
 is the particle’s electric charge,
is the particle’s electric charge,  is the particle’s mass,
is the particle’s mass, 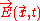 is the self-consistent electric field
is the self-consistent electric fieldElectric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
,
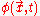 the self-consistent electric potential
the self-consistent electric potentialElectric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
and
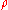 is the electric charge
is the electric chargeElectric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
density.
Vlasov–Poisson equations are used to describe various phenomena in plasma, in particular Landau damping
Landau damping
In physics, Landau damping, named after its discoverer, the eminent Soviet physicist Lev Davidovich Landau, is the effect of damping of longitudinal space charge waves in plasma or a similar environment. This phenomenon prevents an instability from developing, and creates a region of stability in...
and the distributions in a double layer
Double layer (plasma)
A double layer is a structure in a plasma and consists of two parallel layers with opposite electrical charge. The sheets of charge cause a strong electric field and a correspondingly sharp change in voltage across the double layer. Ions and electrons which enter the double layer are accelerated,...
plasma, where they are necessarily strongly non-, and therefore inaccessible to fluid models.
Moment equations
In fluid descriptions of plasmas (see plasma modelingPlasma modeling
Plasma Modeling refers to solving equations of motion that describe the state of a plasma. It is generally coupled with Maxwell's Equations for electromagnetic fields...
and magnetohydrodynamics
Magnetohydrodynamics
Magnetohydrodynamics is an academic discipline which studies the dynamics of electrically conducting fluids. Examples of such fluids include plasmas, liquid metals, and salt water or electrolytes...
(MHD))
one does not consider the velocity
distribution. This is achieved by replacing
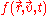 with plasma moments such as number density,
with plasma moments such as number density,  , mean velocity,
, mean velocity,  and pressure,
and pressure, 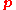
. They are named plasma moments because the nth
moment of
 can be found by integrating
can be found by integrating 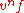 over velocity.
over velocity.These variables are only functions of position and time, which means
that some information is lost. In multifluid theory, the different particle
species are treated as different fluids with different pressures,
densities and flow velocities. The equations governing the plasma moments are called the moment or fluid equations.
Below the two most used moment equations are presented (in SI units). Deriving the moment equations from
the Vlasov equation requires no assumptions about the distribution function.
Continuity equation
The continuity equation describes how the density changes with time.It can be found by integration of the Vlasov equation over the entire
velocity space.
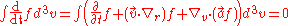
After some calculations, one ends up with
 .
.The particle density
 , and the average velocity
, and the average velocity  , are zeroth and first order moments:
, are zeroth and first order moments: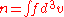
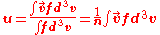
Momentum equation
The rate of change of momentum of a particle is given by the Lorentzequation:
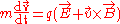
By using this equation and the Vlasov Equation, the momentum equation for each fluid
becomes
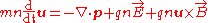 ,
,where
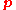 is the pressure tensor. The total time derivative
is the pressure tensor. The total time derivativeTotal derivative
In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
is
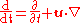 .
.The pressure tensor is defined as the mass density times the covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
of the velocity:
-
 .
.
The frozen-in approximation
As for ideal MHD, the plasma can be considered as tied to the magnetic field lines when certain conditions are fulfilled. One often say that the magnetic field lines are frozen into the plasma. The frozen-in conditions can be derived from Vlasov equation.
We introduce the scales ,
, 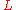 and
and  for time, distance and speed respectively. They represent magnitudes of the different parameters which give large changes in
for time, distance and speed respectively. They represent magnitudes of the different parameters which give large changes in  . By large we mean that
. By large we mean that
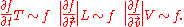
We then write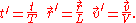
Vlasov equation can now be written
So far no approximations have been done. To be able to proceed we set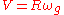 , where
, where 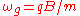 is the gyro frequency and R is the gyroradius. By dividing by
is the gyro frequency and R is the gyroradius. By dividing by 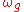 , we get
, we get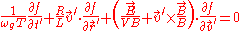
If and
and  , the two first terms will be much less than one since
, the two first terms will be much less than one since 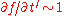 ,
,  and
and 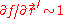 due to the definitions of
due to the definitions of  ,
, 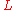 and
and  above. Since the last term is of the order of one, we can neglect the two first terms and write
above. Since the last term is of the order of one, we can neglect the two first terms and write
This equation can be decomposed into a field aligned and a perpendicular part: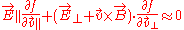
The next step is to write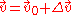 , where
, where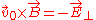
It will soon be clear why this is done. With this substitution, we get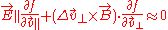
If the parallel electric field is small,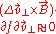
This equation means that the distribution is gyrotropic. The mean velocity of a gyrotropic distribution is zero. Hence,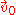 is identical with the mean velocity,
is identical with the mean velocity,  , and we have
, and we have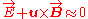
To summarize, the gyro period and the gyro radius must be much smaller than the typical times and lengths which give large changes in the distribution function. The gyro radius is often estimated by replacing with the thermal velocityThermal velocityThe thermal velocity or thermal speed is a typical velocity of the thermal motion of particles which make up a gas, liquid, etc. Thus, indirectly, thermal velocity is a measure of temperature. Technically speaking it is a measure of the width of the peak in the Maxwell-Boltzmann particle velocity...
with the thermal velocityThermal velocityThe thermal velocity or thermal speed is a typical velocity of the thermal motion of particles which make up a gas, liquid, etc. Thus, indirectly, thermal velocity is a measure of temperature. Technically speaking it is a measure of the width of the peak in the Maxwell-Boltzmann particle velocity...
or the Alfvén velocity. In the latter case is often called the inertial length.
is often called the inertial length.
The frozen-in conditions must be evaluated for each particle species separately. Because electrons have much smaller gyro period and gyro radius than ions, the frozen-in conditions will more often be satisfied.
See also
- A. A. Vlasov, Many-Particle Theory and Its Application to Plasma, Gordon and Breach, 1961.

