Vibration of Rotating Structures

Rotating structures - or more general - structures with constant but otherwise arbitrary velocity are important elements of machine

Machine

A machine manages power to accomplish a task, examples include, a mechanical system, a computing system, an electronic system, and a molecular machine. In common usage, the meaning is that of a device having parts that perform or assist in performing any type of work...

ry as rotor shafts and blades of propeller

Propeller

A propeller is a type of fan that transmits power by converting rotational motion into thrust. A pressure difference is produced between the forward and rear surfaces of the airfoil-shaped blade, and a fluid is accelerated behind the blade. Propeller dynamics can be modeled by both Bernoulli's...

s, helicopter

Helicopter

A helicopter is a type of rotorcraft in which lift and thrust are supplied by one or more engine-driven rotors. This allows the helicopter to take off and land vertically, to hover, and to fly forwards, backwards, and laterally...

s or wind turbine

Wind turbine

A wind turbine is a device that converts kinetic energy from the wind into mechanical energy. If the mechanical energy is used to produce electricity, the device may be called a wind generator or wind charger. If the mechanical energy is used to drive machinery, such as for grinding grain or...

s.

Vibrations in such structures require special attention.

Gyroscopic matrices

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

are to be added to classical matrices of mass

Mass

Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...

, damping

Damping

In physics, damping is any effect that tends to reduce the amplitude of oscillations in an oscillatory system, particularly the harmonic oscillator.In mechanics, friction is one such damping effect...

 and stiffness

Stiffness

Stiffness is the resistance of an elastic body to deformation by an applied force along a given degree of freedom when a set of loading points and boundary conditions are prescribed on the elastic body.-Calculations:...

.

The equation

Equation

An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...

 of vibration read:

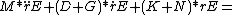
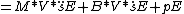
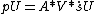
where:

M,D,K classical matrices: mass matrix, damping matrix

Damping matrix

In applied mathematics, a damping matrix is a matrix corresponding to any of certain systems of linear ordinary differential equations.A damping matrix is defined as follows...

 and stiffness matrix
G gyroscopic matrix of vibration velocity
(includes e.g. coriolis

Coriolis effect

In physics, the Coriolis effect is a deflection of moving objects when they are viewed in a rotating reference frame. In a reference frame with clockwise rotation, the deflection is to the left of the motion of the object; in one with counter-clockwise rotation, the deflection is to the right...

 elements)
N gyroscopic matrix of elastic deflection

Deflection (engineering)

In engineering, deflection is the degree to which a structural element is displaced under a load. It may refer to an angle or a distance.The deflection distance of a member under a load is directly related to the slope of the deflected shape of the member under that load and can be calculated by...

(includes e.g. centrifugal elements)
B gyroscopic matrix of small footpoint excitation
A gyroscopic matrix of the structure if it is not
vibrating
V transposition matrix (consists of distances between grid-
and foot- point)
rE small grid point deflection, components measured
relative to moving structure (non inertial)
sE small foot- or reference- point excitation movement,
components measured relativ to an inertial point
(important for connection of non rotating structures)
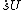(large)constant velocity of
structure foot point
pE variable external loads
pU constant load on grid points due to 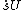, required
for stiffness corrections due to constant initial
deformations
all gyroscopic matrices depend on .
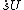Further they contain inertia terms and distances of the structure.
Details are given in the references.

These equations are directly comparable with classical equations of non rotating structures and therefore directly applicable to available solution routines. No other physics

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

 is required, all specialities of rotating masses are included in the gyroscopic matrices. Straight forward coupling with non rotating structures is possible.

For the most simple case (one grid point, D=K=0) it results a gyro

Gyroscope

A gyroscope is a device for measuring or maintaining orientation, based on the principles of angular momentum. In essence, a mechanical gyroscope is a spinning wheel or disk whose axle is free to take any orientation...

 (spinning wheel) with the eigenvalues:

0 for the deflection in direction of - and for rotation around of - the rotating axis. 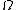the rotation speed for the other translatory deflections. 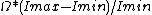the inverse of the Euler period

Frequency

Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...

 for one rotatory deflection.

The last eigenvalue depends on the studied degree of freedom. For sE=0 one gets 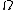from the left side of the equation of movement. For rE=0 one gets the inverse Euler period from the right side. sE=0 means fixed foot point. rE=0 allows a movement of the foot- (reference-) point. Eigenvectors describe circles, coupling 2 translatory or 2 rotatory deflections.