Univalent function
Encyclopedia
In mathematics
, in the branch of complex analysis
, a holomorphic function
on an open subset of the complex plane
is called univalent if it is one-to-one
.
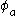of the open unit disc to itself, :
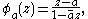where 
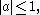is univalent.
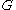and 
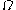are two open connected
sets in the complex plane, and
is a univalent function such that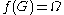
(that is, 
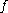is onto), then the derivative of 
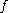is never zero, 
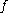is invertible, and its inverse 
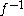is also holomorphic. More, one has by the chain rule
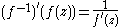
for all
in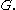 
analytic function
s, unlike for complex analytic (that is, holomorphic) functions, these statements fail to hold. For example, consider the function
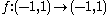
given by ƒ(x) = x3. This function is clearly one-to-one, however, its derivative is 0 at x = 0, and its inverse is not analytic, or even differentiable, on the whole interval (−1, 1).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the branch of complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
on an open subset of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
is called univalent if it is one-to-one
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
.
Examples
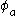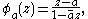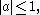Any mapping of the open unit disc to itself, : where is univalent.Basic properties
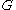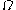One can prove that if and are two open connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
sets in the complex plane, and
is a univalent function such that
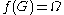(that is, 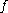is onto), then the derivative of 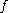is never zero, 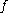is invertible, and its inverse 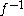is also holomorphic. More, one has by the chain ruleChain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
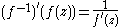
for all
in 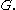Comparison with real functions
For realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s, unlike for complex analytic (that is, holomorphic) functions, these statements fail to hold. For example, consider the function
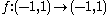
given by ƒ(x) = x3. This function is clearly one-to-one, however, its derivative is 0 at x = 0, and its inverse is not analytic, or even differentiable, on the whole interval (−1, 1).