
Toric section
Encyclopedia
A toric section is an intersection of a plane
with a torus
, just as a conic section
is the intersection of a plane
with a cone
.
s of the form
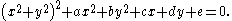
, in which the intersecting plane is parallel to the rotational symmetry axis of the torus
. They were discovered by the ancient Greek geometer Perseus
in roughly 150 BC
. Well-known examples include the hippopede
and the Cassini oval
and their relatives, such as the lemniscate of Bernoulli
.
, in which the intersection is a circle despite the lack of any of the obvious sorts of symmetry that would entail a circular cross-section.
can be created when the intersecting plane is perpendicular
or oblique
to the rotational symmetry axis.
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
with a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, just as a conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
is the intersection of a plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
with a cone
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
.
Mathematical formulae
In general, toric sections are fourth-order (quartic) plane curvePlane curve
In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
s of the form
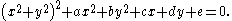
Spiric sections
A special case of a toric section is the spiric sectionSpiric section
In geometry, a spiric section, sometimes called a spiric of Perseus, is a quartic plane curve defined by equations of the form^2=dx^2+ey^2+f....
, in which the intersecting plane is parallel to the rotational symmetry axis of the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
. They were discovered by the ancient Greek geometer Perseus
Perseus (geometer)
Perseus was an ancient Greek geometer, who invented the concept of spiric sections, in analogy to the conic sections studied by Apollonius of Perga....
in roughly 150 BC
150 BC
Year 150 BC was a year of the pre-Julian Roman calendar. At the time it was known as the Year of the Consulship of Flamininus and Balbus...
. Well-known examples include the hippopede
Hippopede
In geometry, a hippopede is a plane curve determined by an equation of the form^2=cx^2+dy^2,...
and the Cassini oval
Cassini oval
A Cassini oval is a plane curve defined as the set of points in the plane such that the product of the distances to two fixed points is constant. This is related to an ellipse, for which the...
and their relatives, such as the lemniscate of Bernoulli
Lemniscate of Bernoulli
In geometry, the lemniscate of Bernoulli is a plane curve defined from two given points F1 and F2, known as foci, at distance 2a from each other as the locus of points P so that PF1·PF2 = a2. The curve has a shape similar to the numeral 8 and to the ∞ symbol. Its name is from lemniscus, which is...
.
Villarceau circles
Another special case is the Villarceau circlesVillarceau circles
In geometry, Villarceau circles are a pair of circles produced by cutting a torus diagonally through the center at the correct angle. Given an arbitrary point on a torus, four circles can be drawn through it. One is in the plane parallel to the equatorial plane of the torus. Another is...
, in which the intersection is a circle despite the lack of any of the obvious sorts of symmetry that would entail a circular cross-section.
General toric sections
More complicated figures such as an annulusAnnulus (mathematics)
In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
can be created when the intersecting plane is perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
or oblique
Oblique
Oblique may refer to:*Oblique angle, in geometry, an angle that is not a multiple of 90 degrees*Oblique angle, synonym for Dutch angle, a cinematographic technique*Oblique , by jazz vibraphonist Bobby Hutcherson...
to the rotational symmetry axis.

