
Villarceau circles
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, Villarceau circles (icon) are a pair of circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s produced by cutting a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
diagonally through the center at the correct angle. Given an arbitrary point on a torus, four circles can be drawn through it. One is in the plane (containing the point) parallel to the equatorial plane of the torus. Another is perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to it. The other two are Villarceau circles. They are named after the French astronomer
Astronomer
An astronomer is a scientist who studies celestial bodies such as planets, stars and galaxies.Historically, astronomy was more concerned with the classification and description of phenomena in the sky, while astrophysics attempted to explain these phenomena and the differences between them using...
and mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Yvon Villarceau
Yvon Villarceau
Antoine-Joseph Yvon Villarceau was a French astronomer, mathematician, and engineer.He constructed an equatorial meridian-instrument and an isochronometric regulator for the Paris Observatory.He wrote Mecanique Celeste...
(1813–1883).
Example
For example, let the torus be given implicitly as the set of points on circles of radius three around points on a circle of radius five in the xy plane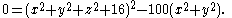
Slicing with the z = 0 plane produces two concentric
Concentric
Concentric objects share the same center, axis or origin with one inside the other. Circles, tubes, cylindrical shafts, disks, and spheres may be concentric to one another...
circles, x2 + y2 = 22 and x2 + y2 = 82. Slicing with the x = 0 plane produces two side-by-side circles, (y − 5)2 + z2 = 32 and (y + 5)2 + z2 = 32.
Two example Villarceau circles can be produced by slicing with the plane 3x = 4z. One is centered at (0, +3, 0) and the other at (0, −3, 0); both have radius five. They can be written in parametric
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
form as
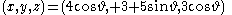
and
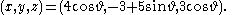
The slicing plane is chosen to be tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to the torus while passing through its center. Here it is tangent at (16⁄5, 0, 12⁄5) and at (−16⁄5, 0, −12⁄5). The angle of slicing is uniquely determined by the dimensions of the chosen torus, and rotating any one such plane around the vertical gives all of them for that torus.
Existence and equations
A proof of the circles’ existence can be constructed from the fact that the slicing plane is tangent to the torus at two points. One characterization of a torus is that it is a surface of revolutionSurface of revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
. Without loss of generality
Without loss of generality
Without loss of generality is a frequently used expression in mathematics...
, choose a coordinate system so that the axis of revolution is the z axis. Begin with a circle of radius r in the xz plane, centered at (R, 0, 0).
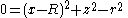
Sweeping replaces x by (x2 + y2)1/2, and clearing the square root produces a quartic equation.
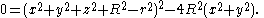
The cross-section of the swept surface in the xz plane now includes a second circle.
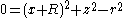
This pair of circles has two common internal tangent lines
Tangent lines to circles
In Euclidean plane geometry, tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs...
, with slope at the origin found from the right triangle with hypotenuse
Hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
R and opposite side r (which has its right angle at the point of tangency). Thus z/x equals ±r / (R2 − r2)1/2, and choosing the plus sign produces the equation of a plane bitangent to the torus.
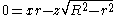
By symmetry, rotations of this plane around the z axis give all the bitangent planes through the center. (There are also horizontal planes tangent to the top and bottom of the torus, each of which gives a “double circle”, but not Villarceau circles.)
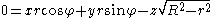
We can calculate the intersection of the plane(s) with the torus analytically, and thus show that the result is a symmetric pair of circles, one of which is a circle of radius R centered at
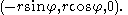
A treatment along these lines can be found in Coxeter (1969).
A more abstract — and more flexible — approach was described by Hirsch (2002), using algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
in a projective setting. In the homogeneous quartic equation for the torus,
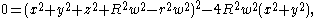
setting w to zero gives the intersection with the “plane at infinity”, and reduces the equation to
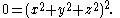
This intersection is a double point, in fact a double point counted twice. Furthermore, it is included in every bitangent plane. The two points of tangency are also double points. Thus the intersection curve, which theory says must be a quartic, contains four double points. But we also know that a quartic with more than three double points must factor (it cannot be irreducible
Irreducible (mathematics)
In mathematics, the concept of irreducibility is used in several ways.* In abstract algebra, irreducible can be an abbreviation for irreducible element; for example an irreducible polynomial....
), and by symmetry the factors must be two congruent conics
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
. Hirsch extends this argument to any surface of revolution generated by a conic, and shows that intersection with a bitangent plane must produce two conics of the same type as the generator when the intersection curve is real.
Filling space
The torus plays a central role in the Hopf fibration of the 3-sphere, S3, over the ordinary sphere, S2, which has circles, S1, as fibers. When the 3-sphere is mapped to Euclidean 3-spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
by stereographic projection
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
, the inverse image of a circle of latitude on S2 under the fiber map is a torus, and the fibers themselves are Villarceau circles. Banchoff
Thomas Banchoff
Thomas Francis Banchoff is an American mathematicianspecializing in geometry. He is a professor at Brown University, where he has taught since 1967...
(1990) has explored such a torus with computer graphics imagery. One of the unusual facts about the circles is that each links through all the others, not just in its own torus but in the collection filling all of space; Berger (1987) has a discussion and drawing.
External links
- Torus at MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
- Flat Torus in the Three-Sphere The circles of the torus (Les cercles du tore)

