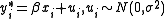Tobit model
Encyclopedia
The Tobit model is a statistical model
proposed by James Tobin
(1958) to describe the relationship between a non-negative dependent variable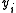 and an independent variable (or vector)
and an independent variable (or vector) 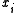 .
.
The model supposes that there is a latent (i.e. unobservable) variable
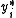 . This variable linearly depends on
. This variable linearly depends on 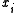 via a parameter (vector)
via a parameter (vector) 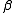 which determines the relationship between the independent variable (or vector)
which determines the relationship between the independent variable (or vector) 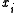 and the latent variable
and the latent variable
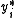 (just as in a linear model
(just as in a linear model
). In addition, there is a normally distributed error term
 to capture random influences on this relationship. The observable variable
to capture random influences on this relationship. The observable variable 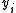 is defined to be equal to the latent variable whenever the latent variable is above zero and zero otherwise.
is defined to be equal to the latent variable whenever the latent variable is above zero and zero otherwise.
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
proposed by James Tobin
James Tobin
James Tobin was an American economist who, in his lifetime, served on the Council of Economic Advisors and the Board of Governors of the Federal Reserve System, and taught at Harvard and Yale Universities. He developed the ideas of Keynesian economics, and advocated government intervention to...
(1958) to describe the relationship between a non-negative dependent variable
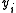 and an independent variable (or vector)
and an independent variable (or vector) 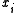 .
.The model supposes that there is a latent (i.e. unobservable) variable
Latent variable
In statistics, latent variables , are variables that are not directly observed but are rather inferred from other variables that are observed . Mathematical models that aim to explain observed variables in terms of latent variables are called latent variable models...
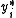 . This variable linearly depends on
. This variable linearly depends on 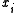 via a parameter (vector)
via a parameter (vector) 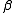 which determines the relationship between the independent variable (or vector)
which determines the relationship between the independent variable (or vector) 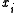 and the latent variable
and the latent variableLatent variable
In statistics, latent variables , are variables that are not directly observed but are rather inferred from other variables that are observed . Mathematical models that aim to explain observed variables in terms of latent variables are called latent variable models...
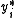 (just as in a linear model
(just as in a linear modelLinear model
In statistics, the term linear model is used in different ways according to the context. The most common occurrence is in connection with regression models and the term is often taken as synonymous with linear regression model. However the term is also used in time series analysis with a different...
). In addition, there is a normally distributed error term
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
 to capture random influences on this relationship. The observable variable
to capture random influences on this relationship. The observable variable 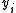 is defined to be equal to the latent variable whenever the latent variable is above zero and zero otherwise.
is defined to be equal to the latent variable whenever the latent variable is above zero and zero otherwise.-
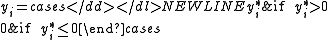
where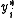 is a latent variable:
is a latent variable:
Consistency
If the relationship parameter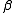 is estimated by regressing the observed
is estimated by regressing the observed 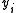 on
on  , the resulting ordinary least squaresLeast squaresThe method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
, the resulting ordinary least squaresLeast squaresThe method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
regression estimator is inconsistentConsistency (statistics)In statistics, consistency of procedures such as confidence intervals or hypothesis tests involves their behaviour as the number of items in the data-set to which they are applied increases indefinitely...
. It will yield a downwards-biased estimate of the slope coefficient and an upwards-biased estimate of the intercept. Takeshi AmemiyaTakeshi Amemiyais an economist specializing in econometrics and the economy of ancient Greece.Amemiya is the Edward Ames Edmonds Professor of Economics and a Professor of Classics at Stanford University...
(1973) has proven that the maximum likelihood estimator suggested by Tobin for this model is consistent.
Interpretation
The coefficient should not be interpreted as the effect of
coefficient should not be interpreted as the effect of  on
on 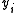 , as one would with a linear regression model; this is a common error. Instead, it should be interpreted as the combination of (1) the change in
, as one would with a linear regression model; this is a common error. Instead, it should be interpreted as the combination of (1) the change in  of those above the limit, weighted by the probability of being above the limit; and (2) the change in the probability of being above the limit, weighted by the expected value of
of those above the limit, weighted by the probability of being above the limit; and (2) the change in the probability of being above the limit, weighted by the expected value of 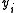 if above.
if above.
Variations of the Tobit model
Variations of the Tobit model can be produced by changing where and when censoring occurs. Amemiya (1985) classifies these variations into five categories (Tobit type I - Tobit type V), where Tobit type I stands for the first model described above. Schnedler (2005) provides a general formula to obtain consistent likelihood estimators for these and other variations of the Tobit model.
Type I
The Tobit model is a special case of a censored regression modelCensored regression modelCensored regression models commonly arise in econometrics in cases where the variable ofinterest is only observable under certain conditions. A common example is labor supply. Data are frequently available on the hours worked by employees, and a labor supply model estimates the relationship between...
, because the latent variable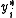 cannot always be observed while the independent variable
cannot always be observed while the independent variable 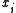 is observable. A common variation of the Tobit model is censoring at a value
is observable. A common variation of the Tobit model is censoring at a value 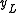 different from zero:
different from zero:
-
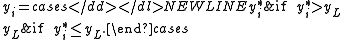
Another example is censoring of values above .
.
-
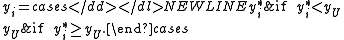
Yet another model results when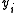 is censored from above and below at the same time.
is censored from above and below at the same time.
-

The rest of the models will be presented as being bounded from below at 0, though this can be generalized as we have done for Type I.
Type II
Type II Tobit models introduce a second latent variable.
-
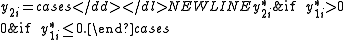
Heckman (1987) falls into the Type II Tobit. In Type I Tobit, the latent variable absorb both the process of participation and 'outcome' of interest. Type II Tobit allows the process of participation/selection and the process of 'outcome' to be independent, conditional on x.
Type III
Type III introduces a second observed dependent variable.-
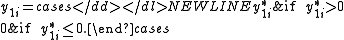
-

The HeckmanHeckman correctionThe Heckman correction is any of a number of related statistical methods developed by James Heckman in 1976 through 1979 which allow the researcher to correct for selection bias...
model falls into this type.
Type IV
Type IV introduces a third observed dependent variable and a third latent variable.-
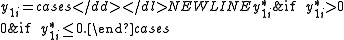
-

-
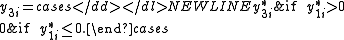
Type V
Similar to Type II, in Type V we only observe the sign of .
.
-
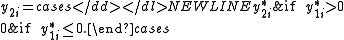
-
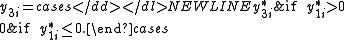
The likelihood function
Below are the likelihoodLikelihood functionIn statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
and log likelihood functions for a type I Tobit. This is a Tobit that is censored from below at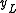 when the latent variable
when the latent variable 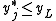 . In writing out the likelihood function, we first define an indicator function
. In writing out the likelihood function, we first define an indicator function 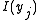 where:
where:
-
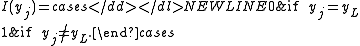
Next, we mean to be the standard normal cumulative distribution functionCumulative distribution functionIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
to be the standard normal cumulative distribution functionCumulative distribution functionIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
and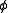 to be the standard normal probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
to be the standard normal probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
. For a data set with N observations the likelihood function for a type I Tobit is
-
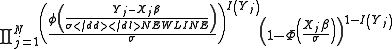
Etymology
The term “tobit” was derived from Tobin's name and by adding the suffix "-it," as for the 1964 probit modelProbit modelIn statistics, a probit model is a type of regression where the dependent variable can only take two values, for example married or not married....
by Arthur GoldbergerArthur GoldbergerArthur Stanley Goldberger was an econometrician and an economist. He worked with Nobel Prize winner Lawrence Klein on the development of the famous Klein–Goldberger macroeconomic computer model at the University of Michigan...
.
External links
-
-
-
-
-
-
-
-
-
-
-
-
-