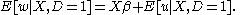Heckman correction
Encyclopedia
The Heckman correction is any of a number of related statistical methods developed by James Heckman
in 1976 through 1979 which allow the researcher to correct for selection bias
. Selection bias problems are endemic to applied econometric
problems, which make Heckman’s original technique, and subsequent refinements by both himself and others, indispensable to applied econometricians. In 2000 Heckman received the Economics Nobel Prize
for this achievement while working at the University of Chicago
.
Heckman discussed bias from using nonrandom selected samples to estimate behavioral relationships as a specification error. He suggests a two-stage estimation method to correct the bias. The correction is easy to implement and has a firm basis in statistical theory. Heckman’s correction involves a normality assumption, provides a test for sample selection bias and formula for bias corrected model.
Suppose that a researcher wants to estimate the determinants of wage offers, but has access to wage observations for only those who work. Since people who work are selected non-randomly from the population, estimating the determinants of wages from the subpopulation who work may introduce bias. The Heckman correction takes place in two stages. First, the researcher formulates a model, based on economic theory, for the probability of working. The canonical specification for this relationship is a probit
regression of the form
where D indicates employment (D = 1 if the respondent is employed and D = 0 otherwise), Z is a vector of explanatory variables,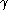
is a vector of unknown parameters, and Φ is the cumulative distribution function
of the standard normal distribution. Estimation of the model yields results that can be used to predict this probability for each individual. In the second stage, the researcher corrects for self-selection by incorporating a transformation of these predicted individual probabilities as an additional explanatory variable. The wage equation may be specified,
where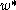
denotes an underlying wage offer, which is not observed if the respondent does not work. The conditional expectation of wages given the person works is then
Under the assumption that the error terms
are jointly normal, we have
where ρ is the correlation between unobserved determinants of propensity to work
and unobserved determinants of wage offers u, σ u is the standard deviation of 
, and 
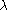is the inverse Mills ratio
evaluated at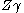
. This equation demonstrates Heckman's insight that sample selection can be viewed as a form of omitted-variables bias, as conditional on both X and on 
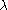it is as if the sample is randomly selected. The wage equation can be estimated by replacing 
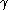with Probit estimates from the first stage, constructing the 
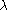term, and including it as an additional explanatory variable in linear regression
estimation of the wage equation. Since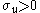
, the coefficient on 
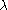can only be zero if 
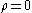, so testing the null that the coefficient on 
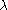is zero is equivalent to testing for sample selectivity.
Heckman's achievements have generated a large number of empirical applications in economics as well as in other social sciences. The original method has subsequently been generalized, by Heckman and by others.
James Heckman
James Joseph Heckman is an American economist and Nobel laureate. He is the Henry Schultz Distinguished Service Professor of Economics at the University of Chicago, Professor of Science and Society at University College Dublin and a Senior Research Fellow at the American Bar Foundation.Heckman...
in 1976 through 1979 which allow the researcher to correct for selection bias
Selection bias
Selection bias is a statistical bias in which there is an error in choosing the individuals or groups to take part in a scientific study. It is sometimes referred to as the selection effect. The term "selection bias" most often refers to the distortion of a statistical analysis, resulting from the...
. Selection bias problems are endemic to applied econometric
Econometrics
Econometrics has been defined as "the application of mathematics and statistical methods to economic data" and described as the branch of economics "that aims to give empirical content to economic relations." More precisely, it is "the quantitative analysis of actual economic phenomena based on...
problems, which make Heckman’s original technique, and subsequent refinements by both himself and others, indispensable to applied econometricians. In 2000 Heckman received the Economics Nobel Prize
Nobel Memorial Prize in Economic Sciences
The Nobel Memorial Prize in Economic Sciences, commonly referred to as the Nobel Prize in Economics, but officially the Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel , is an award for outstanding contributions to the field of economics, generally regarded as one of the...
for this achievement while working at the University of Chicago
University of Chicago
The University of Chicago is a private research university in Chicago, Illinois, USA. It was founded by the American Baptist Education Society with a donation from oil magnate and philanthropist John D. Rockefeller and incorporated in 1890...
.
The Method
Statistical analyses based on those non-randomly selected samples can lead to erroneous conclusions and poor policy. The Heckman correction, a two-step statistical approach, offers a means of correcting for non-randomly selected samples.Heckman discussed bias from using nonrandom selected samples to estimate behavioral relationships as a specification error. He suggests a two-stage estimation method to correct the bias. The correction is easy to implement and has a firm basis in statistical theory. Heckman’s correction involves a normality assumption, provides a test for sample selection bias and formula for bias corrected model.
Suppose that a researcher wants to estimate the determinants of wage offers, but has access to wage observations for only those who work. Since people who work are selected non-randomly from the population, estimating the determinants of wages from the subpopulation who work may introduce bias. The Heckman correction takes place in two stages. First, the researcher formulates a model, based on economic theory, for the probability of working. The canonical specification for this relationship is a probit
Probit
In probability theory and statistics, the probit function is the inverse cumulative distribution function , or quantile function associated with the standard normal distribution...
regression of the form
where D indicates employment (D = 1 if the respondent is employed and D = 0 otherwise), Z is a vector of explanatory variables,
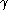is a vector of unknown parameters, and Φ is the cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of the standard normal distribution. Estimation of the model yields results that can be used to predict this probability for each individual. In the second stage, the researcher corrects for self-selection by incorporating a transformation of these predicted individual probabilities as an additional explanatory variable. The wage equation may be specified,
where
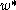denotes an underlying wage offer, which is not observed if the respondent does not work. The conditional expectation of wages given the person works is then
Under the assumption that the error terms
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
are jointly normal, we have
where ρ is the correlation between unobserved determinants of propensity to work
and unobserved determinants of wage offers u, σ u is the standard deviation of , and 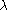is the inverse Mills ratioInverse Mills ratio
In statistics, the inverse Mills ratio, named after John P. Mills, is the ratio of the probability density function to the cumulative distribution function of a distribution....
evaluated at
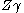. This equation demonstrates Heckman's insight that sample selection can be viewed as a form of omitted-variables bias, as conditional on both X and on 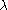it is as if the sample is randomly selected. The wage equation can be estimated by replacing 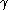with Probit estimates from the first stage, constructing the 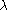term, and including it as an additional explanatory variable in linear regressionOLS
OLS can stand for:* IATA code for Nogales International Airport in Arizona* Ordinary least squares, a method used in regression analysis for estimating linear models* Ottawa Linux Symposium* Oulun Luistinseura...
estimation of the wage equation. Since
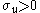, the coefficient on 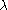can only be zero if 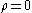, so testing the null that the coefficient on 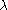is zero is equivalent to testing for sample selectivity.Heckman's achievements have generated a large number of empirical applications in economics as well as in other social sciences. The original method has subsequently been generalized, by Heckman and by others.
Disadvantages
- The two-step estimator discussed above is a limited information maximum likelihood (LIML) estimator. In asymptotic theory and in finite samples as demonstrated by Monte Carlo simulations, the full information (FIML) estimator exhibits better statistical properties. However, the FIML estimator is more computationally difficult to implement.
- The covariance matrix generated by OLS estimation of the second stage is inconsistent. Correct standard errors and other statistics can be generated from an asymptotic approximation or by resampling, such as through a bootstrap.
- The canonical model assumes the errors are jointly normal. If that assumption fails, the estimator is generally inconsistent and can provide misleading inference in small samples. Semiparametric and other robust alternatives can be used in such cases.
- The model obtains formal identification from the normality assumption when the same covariates appear in the selection equation and the equation of interest, but identification will be tenuous unless there are many observations in the tails where there is substantial nonlinearity in the Inverse Mills Ratio. Generally, an exclusion restriction is required to generate credible estimates: there must be at least one variable which appears with a non-zero coefficient in the selection equation but does not appear in the equation of interest, essentially an instrumentInstrumental variableIn statistics, econometrics, epidemiology and related disciplines, the method of instrumental variables is used to estimate causal relationships when controlled experiments are not feasible....
. If no such variable is available, it may be difficult to correct for sampling selectivity.
External links
- Encyclopedia Britannica article
- Article on Heckman-MacFadden Nobel Prize.
- Nobel prize official description.