Thermal quantum field theory
Encyclopedia
In theoretical physics
, thermal quantum field theory or finite temperature field theory (or, shorter,
thermal field theory) is a set of methods to calculate expectation values of physical observables of a quantum field theory
at finite temperature
.
In the Matsubara (imaginary-time) formalism,
the basic idea (due to Felix Bloch
) is that the expectation values of operators in a thermal ensemble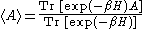
may be written as expectation values in ordinary quantum field theory
where the configuration is evolved by an imaginary time
. One can therefore switch to
a spacetime
with Euclidean signature, where the
above trace (Tr) leads to the requirement that all boson
ic and fermion
ic
fields be periodic and antiperiodic, respectively, with respect to
the Euclidean time direction with periodicity
(we are assuming natural units
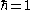). This allows
one to perform calculations with the same tools as in ordinary quantum field theory,
such as functional integrals and Feynman diagram
s, but with compact Euclidean time. Note that the definition of normal ordering has to be altered .
In momentum space, this leads to the replacement of continuous frequencies by
discrete imaginary (Matsubara) frequencies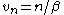
and, through the de Broglie relation, to a discretized thermal energy spectrum 
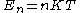. This has been shown to be a useful tool
in studying the behavior of quantum field theories at finite temperature
.
It has been generalized to theories with gauge invariance and was a central tool
in the study of a conjectured deconfining phase transition of Yang-Mills theory
.
In this Euclidean field theory, real-time observables can be retrieved
by analytic continuation
.
The alternative to the use of fictitious imaginary times is to use a real-time formalism which come in two forms. A path-ordered approach to real-time formalisms includes the Schwinger-Keldysh formalism
and more modern variants.
The latter involves replacing a straight time contour from (large negative) real
initial time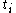
to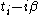 
by one that first runs to (large positive) real time 
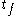and then suitably back to 
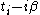. The piecewise composition
of the resulting complex time contour leads to a doubling of fields and more complicated
Feynman rules, but obviates the need of analytic continuation
s of the imaginary-time formalism. The alternative approach to real-time formalisms is an operator based approach using Bogoliubov transformation
s, known as Thermo Field Dynamics.
As well as Feynman diagrams and perturbation theory, other techniques such as dispersion relations
and the finite temperature analog of Cutkosky rules can also be used in the real time formulation
.
An alternative approach which is of interest to mathematical physics is to work with
KMS state
s.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, thermal quantum field theory or finite temperature field theory (or, shorter,
thermal field theory) is a set of methods to calculate expectation values of physical observables of a quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
at finite temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
.
In the Matsubara (imaginary-time) formalism,
the basic idea (due to Felix Bloch
Felix Bloch
Felix Bloch was a Swiss physicist, working mainly in the U.S.-Life and work:Bloch was born in Zürich, Switzerland to Jewish parents Gustav and Agnes Bloch. He was educated there and at the Eidgenössische Technische Hochschule, also in Zürich. Initially studying engineering he soon changed to physics...
) is that the expectation values of operators in a thermal ensemble
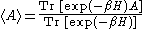
may be written as expectation values in ordinary quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
where the configuration is evolved by an imaginary time
Imaginary time
Imaginary time is a concept derived from quantum mechanics and is essential in connecting quantum mechanics with statistical mechanics.- In quantum mechanics :...
. One can therefore switch toa spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
with Euclidean signature, where the
above trace (Tr) leads to the requirement that all boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
ic and fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
ic
fields be periodic and antiperiodic, respectively, with respect to
the Euclidean time direction with periodicity
(we are assuming natural unitsNatural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
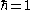). This allowsone to perform calculations with the same tools as in ordinary quantum field theory,
such as functional integrals and Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s, but with compact Euclidean time. Note that the definition of normal ordering has to be altered .
In momentum space, this leads to the replacement of continuous frequencies by
discrete imaginary (Matsubara) frequencies
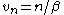and, through the de Broglie relation, to a discretized thermal energy spectrum 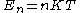. This has been shown to be a useful toolin studying the behavior of quantum field theories at finite temperature
.
It has been generalized to theories with gauge invariance and was a central tool
in the study of a conjectured deconfining phase transition of Yang-Mills theory
.
In this Euclidean field theory, real-time observables can be retrieved
by analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
.
The alternative to the use of fictitious imaginary times is to use a real-time formalism which come in two forms. A path-ordered approach to real-time formalisms includes the Schwinger-Keldysh formalism
Keldysh formalism
In condensed matter physics, the Keldysh formalism is a general framework for describing the quantum mechanical evolution of a system in a non-equilibrium state, e.g. in the presence of time varying fields . The main mathematical object in the Keldysh formalism is the non-equilibrium Green's...
and more modern variants.
The latter involves replacing a straight time contour from (large negative) real
initial time
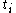to 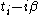by one that first runs to (large positive) real time 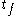and then suitably back to 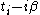. The piecewise compositionof the resulting complex time contour leads to a doubling of fields and more complicated
Feynman rules, but obviates the need of analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
s of the imaginary-time formalism. The alternative approach to real-time formalisms is an operator based approach using Bogoliubov transformation
Bogoliubov transformation
In theoretical physics, the Bogoliubov transformation, named after Nikolay Bogolyubov, is a unitary transformation from a unitary representation of some canonical commutation relation algebra or canonical anticommutation relation algebra into another unitary representation, induced by an...
s, known as Thermo Field Dynamics.
As well as Feynman diagrams and perturbation theory, other techniques such as dispersion relations
and the finite temperature analog of Cutkosky rules can also be used in the real time formulation
.
An alternative approach which is of interest to mathematical physics is to work with
KMS state
KMS state
In the statistical mechanics of quantum mechanical systems and quantum field theory, the properties of a system in thermal equilibrium can be described by a mathematical object called a Kubo-Martin-Schwinger state or, more commonly, a KMS state.-Preliminaries:...
s.