
Tau (2π)
Encyclopedia
Tau is a mathematical constant
equal to the ratio of any circle
's circumference
to its radius
, and has a value of approximately 6.28318531. This number also appears in many common formulas, often because it is the period of some very common functions — sine, cosine, , and others that involve trips around the unit circle
. However, instead of having its own symbol, it has historically been written as 2. Advocates for argue that radius is more fundamental to circles than diameter
, and therefore, that (circumference divided by radius) is more fundamental than (circumference divided by diameter). They think this makes formulas written in terms of express the mathematics more clearly than with . Tau's proponents consider radius more fundamental for the following reasons:
Opponents dispute claims that (or alternatively, 2) occurs more commonly than across mathematics in general. Rather, they say is just more common in some fields, and more common in others. They argue that tau's supporters have focused exclusively on lower-level (grade school to undergraduate) mathematics, which make up only a portion of mathematics in general. Since dividing by 2 is usually considered more complicated — both to perform and to write — than multiplying by 2, the simplicity lost replacing with the fraction in one formula is greater than the simplicity gained replacing 2 with in one formula.
Tau has become the most popular choice for the constant, but opponents argue that the letter has many other unrelated mathematical meanings. Supporters on the other hand state that precisely the fact that several meanings already coexist suggests that this is not problematic.
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
equal to the ratio of any circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
's circumference
Circumference
The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
to its radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
, and has a value of approximately 6.28318531. This number also appears in many common formulas, often because it is the period of some very common functions — sine, cosine, , and others that involve trips around the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
. However, instead of having its own symbol, it has historically been written as 2. Advocates for argue that radius is more fundamental to circles than diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
, and therefore, that (circumference divided by radius) is more fundamental than (circumference divided by diameter). They think this makes formulas written in terms of express the mathematics more clearly than with . Tau's proponents consider radius more fundamental for the following reasons:
- A circle is defined as all pointsPoint (geometry)In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
in a plane a certain distance — the radius — away from a center point. - Standard circle formulas use radius: or ,
- The unit circle — note the word unit — has a radius of 1, not a diameter of 1.
- AngleAngleIn geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s are measured in radians.
Opponents dispute claims that (or alternatively, 2) occurs more commonly than across mathematics in general. Rather, they say is just more common in some fields, and more common in others. They argue that tau's supporters have focused exclusively on lower-level (grade school to undergraduate) mathematics, which make up only a portion of mathematics in general. Since dividing by 2 is usually considered more complicated — both to perform and to write — than multiplying by 2, the simplicity lost replacing with the fraction in one formula is greater than the simplicity gained replacing 2 with in one formula.
Angles and radians
- One radian, the fundamental unit of angle measurement, is the angle a one-radius-length arc subtends on a circle. So the number of radians in a full circle equals the number of one-radius-length arcs around a circle, which is the ratio of a circle's circumference to its radius. This is the definition of .
- Since radians covers a full circle, radians covers a circle, radians covers a circle, and so on. Converting in the opposite direction, a circle has an angle measuring radians, a circle has an angle measuring radians, and so on. So the fraction does not change when converting in either direction.
- By comparison, radians covers a circle, radians covers a circle, and so on. Converting in the opposite direction, a circle has an angle measuring = radians, a circle has an angle measuring = radians, and so on. With , the fraction does change, either multiplying or dividing by 2, depending on the direction of conversion. So using instead of imposes two extra steps, first deciding whether the fraction must be multiplied or divided by 2, then actually doing the multiplication or division.
- The so-called "special angles" that need to be memorized when using
 simply become fractions of a whole circle when using
simply become fractions of a whole circle when using  , e.g.
, e.g.  ,
, 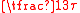 ,
, 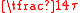 ,
, 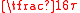 and
and  . It is easier to explain that one eighth of a circle corresponds to
. It is easier to explain that one eighth of a circle corresponds to 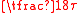 radians than to
radians than to  radians. Hartl describes the use of
radians. Hartl describes the use of  in this context as a "pedagogical disaster".
in this context as a "pedagogical disaster".
Circles, arcs and sectors
- The circle circumferenceCircumferenceThe circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
formula simplifies to
simplifies to  .
. - The circle area formula
 becomes the more complex, but more standard
becomes the more complex, but more standard 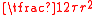 .
. - With
 , both the circumference and area formulas for a circle have forms identical to the arclength
, both the circumference and area formulas for a circle have forms identical to the arclength 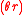 and area
and area 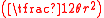 formulas for a circular sectorCircular sectorA circular sector or circle sector, is the portion of a disk enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger being the major sector. In the diagram, θ is the central angle in radians, r the radius of the circle, and L is the arc length of the...
formulas for a circular sectorCircular sectorA circular sector or circle sector, is the portion of a disk enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger being the major sector. In the diagram, θ is the central angle in radians, r the radius of the circle, and L is the arc length of the...
; with , neither formula does. A whole circle is just a circle sector with
, neither formula does. A whole circle is just a circle sector with  , so students could memorize just two formulas instead of four.
, so students could memorize just two formulas instead of four. - The base
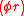 and area
and area 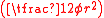 formulas for a skinny triangleSkinny triangleA skinny triangle in trigonometry is a triangle whose height is much greater than its base. The solution of such triangles can be greatly simplified by using the approximation that the sine of a small angle is equal to the angle in radians...
formulas for a skinny triangleSkinny triangleA skinny triangle in trigonometry is a triangle whose height is much greater than its base. The solution of such triangles can be greatly simplified by using the approximation that the sine of a small angle is equal to the angle in radians...
also have those forms. They can be used to derive the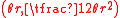 or
or  formula pairs above by cutting a sector or circle into many pizza-style slices and approximating those slices as skinny triangleSkinny triangleA skinny triangle in trigonometry is a triangle whose height is much greater than its base. The solution of such triangles can be greatly simplified by using the approximation that the sine of a small angle is equal to the angle in radians...
formula pairs above by cutting a sector or circle into many pizza-style slices and approximating those slices as skinny triangleSkinny triangleA skinny triangle in trigonometry is a triangle whose height is much greater than its base. The solution of such triangles can be greatly simplified by using the approximation that the sine of a small angle is equal to the angle in radians...
s. The sum of the triangles' vertex angles equals
equals  or
or  so the sum of their bases
so the sum of their bases  equals
equals 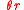 or
or  and the sum of their areas
and the sum of their areas 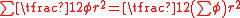 equals
equals 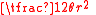 or
or 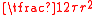
 |
 |
circumference and area of a circle. | |||
 |
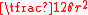 |
arclength and area of a circular sector Circular sector A circular sector or circle sector, is the portion of a disk enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger being the major sector. In the diagram, θ is the central angle in radians, r the radius of the circle, and L is the arc length of the... . |
|||
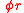 |
 |
base and area of a skinny triangle Skinny triangle A skinny triangle in trigonometry is a triangle whose height is much greater than its base. The solution of such triangles can be greatly simplified by using the approximation that the sine of a small angle is equal to the angle in radians... . |
|||
In physics there are many other examples of this pattern of two important formulas, (1) a constant times a variable, and (2) its integral which is  times the constant times the variable squared. times the constant times the variable squared. |
|||||
 |
 |
velocity and displacement after constant acceleration (starting from rest) |  |
 |
angular velocity and angular displacement after constant angular acceleration (starting from rest) |
 |
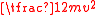 |
momentum and kinetic energy Kinetic energy The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes... |
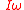 |
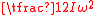 |
angular momentum and rotational energy |
 |
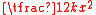 |
spring force applied and spring potential energy |  |
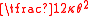 |
torque applied and torsion pendulum potential energy Torsion spring A torsion spring is a spring that works by torsion or twisting; that is, a flexible elastic object that stores mechanical energy when it is twisted. The amount of force it exerts is proportional to the amount it is twisted. There are two types... |
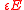 |
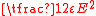 |
electric flux density and electric field energy density |  |
 |
capacitor charge and energy stored |
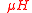 |
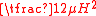 |
magnetic flux density and magnetic field energy density | 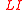 |
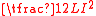 |
inductor flux and energy stored |
Straight lines and polygons
- A straight angle (or the sum of the angles in a linear pair) describes the angle on only one side of a line, which is . The total angle measure on both sides of that line is = + .
- When a transversal intersects two parallel linesParallel (geometry)Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
, the sum of the interior angles on only one side of the transversal is . The sum of the interior angles on both sides of the transversal is = + .
. The sum of the interior angles on both sides of the transversal is = + . - The sum of the exterior angles of a polygon is
 .
. - The sum of the interior angles of a triangle is
 . More generally, the sum of the interior angles of a simple n-gonSimple polygonIn geometry, a simple polygon is a closed polygonal chain of line segments in the plane which do not have points in common other than the common vertices of pairs of consecutive segments....
. More generally, the sum of the interior angles of a simple n-gonSimple polygonIn geometry, a simple polygon is a closed polygonal chain of line segments in the plane which do not have points in common other than the common vertices of pairs of consecutive segments....
is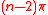 .
. - Each (additional) vertex added to a simple polygon increases its total angle sum by . The increase is always divided equally between the internal and outside angle sums. (outside angle = − internal angle and is not the same as external angle)
-
- Sum of internal angles = − Sum of outside angles = + Sum of internal angles + Sum of outside angles = n
- Area of a regular n-sided polygon inscribed in the unit circle

- Area of a regular n-sided polygon inscribed in the unit circle
- Sum of internal angles = − Sum of outside angles = + Sum of internal angles + Sum of outside angles = n
Functions based on the unit circle
- The unit circle's circumference is
 , but its area is
, but its area is  .
.  proponents argue that the unit circle's circumference is the more important quantity because it becomes the period of the ubiquitous sine, cosine, and complex exponential functions, while
proponents argue that the unit circle's circumference is the more important quantity because it becomes the period of the ubiquitous sine, cosine, and complex exponential functions, while  advocates argue that the use of
advocates argue that the use of  for the area of the unit circle is more elegant.
for the area of the unit circle is more elegant. - The periodicity of the cosine, sineSineIn mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
, and complex exponential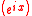 functions is instead of 2, which is simpler and arguably more intuitive.
functions is instead of 2, which is simpler and arguably more intuitive. - The nth roots of unityRoot of unityIn mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
 where k = 0,..,n-1.
where k = 0,..,n-1. - Cauchy's integral formulaCauchy's integral formulaIn mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all...

Euler's Identity
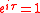 |
When Euler's Identity is written  , it provides the value of the complex exponential of the circle constant. So if tau, not pi, is used, then the name Euler's Identity could apply to the even simpler formula , it provides the value of the complex exponential of the circle constant. So if tau, not pi, is used, then the name Euler's Identity could apply to the even simpler formula 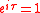 . Although . Although  shows the complex exponential is periodic with period , shows the complex exponential is periodic with period ,  does show more—that the complex exponential is antiperiodic with antiperiod (which also logically implies it is periodic with period 2 = ). does show more—that the complex exponential is antiperiodic with antiperiod (which also logically implies it is periodic with period 2 = ). |
 |
The sum of the nth roots of unity is zero 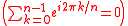 for n ≥ 2. The n = 2 case of this identity for n ≥ 2. The n = 2 case of this identity 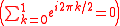 is just Euler's Identity, but with 2/2 instead of is just Euler's Identity, but with 2/2 instead of 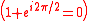 . Tau replaces 2 to produce . Tau replaces 2 to produce 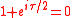 which, unlike which, unlike 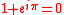 , contains the number 2. In " , contains the number 2. In " is Wrong!", Bob Palais defended this as adding "one more fundamental constant" to Euler's Identity (though he endorsed is Wrong!", Bob Palais defended this as adding "one more fundamental constant" to Euler's Identity (though he endorsed 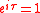 as well). as well). |
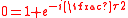 |
The sum of the complex conjugate Complex conjugate In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs... s of the nth roots of unity is also zero for n ≥ 2. Similar analysis to that above produces the identity 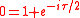 . It has all four basic arithmetic operations in "standard" order . It has all four basic arithmetic operations in "standard" order  ; the numbers ; the numbers 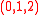 in order; and in order; and  in alphabetical order. As with the changes to Euler's Identity, these issues are not very (and some not at all) important mathematically. But many people have said they dislike tau because they are fond of Euler's Identity (as currently written with pi) for similar reasons. Therefore they may have a non-trivial effect on whether tau replaces pi. in alphabetical order. As with the changes to Euler's Identity, these issues are not very (and some not at all) important mathematically. But many people have said they dislike tau because they are fond of Euler's Identity (as currently written with pi) for similar reasons. Therefore they may have a non-trivial effect on whether tau replaces pi. |
Waves, angular frequency, and the Fourier transform
- WavenumberWavenumberIn the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
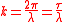
- Angular frequencyAngular frequencyIn physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
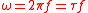
- Frequencies may be more recognisable in the (most common time-periodic) functions sin
 t, cos
t, cos 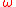 t, and
t, and  .
.
-
- For example sin (876.89
 t) is immediately recognizable as an 876.89 Hz sine wave while sin (1753.78
t) is immediately recognizable as an 876.89 Hz sine wave while sin (1753.78  t) is not.
t) is not. - For sums of harmonic terms (like Fourier series), identifying which term is the 6th harmonic is quicker and less error-prone when they're written
 instead of
instead of  .
.
- Reduced Planck constant

- Inductor impedance
 (where
(where  represents the imaginary unitImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
represents the imaginary unitImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
usually represented by )
) - Capacitor impedance
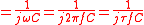
- Reduced Planck constant
- For example sin (876.89
Fourier transform, using ordinary frequency
- Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
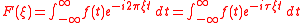
- Inverse Fourier transform
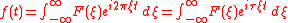
Common Fourier Transform Pairs Containing 2 = 


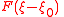
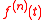
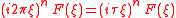


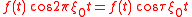
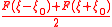
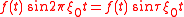

Fourier transform, using angular frequency, unitary
- Fourier transform

- Inverse Fourier transform
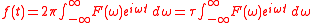
Fourier transform, using angular frequency, non-unitary
- Fourier transform
 (NO CHANGE WITH TAU)
(NO CHANGE WITH TAU) - Inverse Fourier transform

Other areas of mathematics
- Gaussian distribution
- Stirling's approximationStirling's approximationIn mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...

- 2 theorem
- The famous Feynman pointFeynman pointThe Feynman point is a sequence of six 9s that begins at the 762nd decimal place of the decimal representation of . It is named after physicist Richard Feynman, who once stated during a lecture he would like to memorize the digits of until that point, so he could recite them and quip "nine nine...
(six consecutive 9s early in the decimal digits of ) appears one digit earlier in , and is seven digits long instead of six (3.14...349999998... * 2 = 6.28...699999996...).
Distant past
- Islamic mathematicians like al-Kashi (c. 1380–1429) focused on the circle constant 6.283... although they were fully aware of the work of Archimedes focusing on the circle constant that is nowadays called
 .
. - David Gregory
- William Jones
- Leonhard EulerLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
- Paul Matthieu Hermann LaurentPaul Matthieu Hermann LaurentPaul Matthieu Hermann Laurent was a French mathematician. Despite his large body of works, Laurent series expansions for complex functions were not named after him, but after Pierre Alphonse Laurent.-External links:...
; Traité D'Algebra - Fred HoyleFred HoyleSir Fred Hoyle FRS was an English astronomer and mathematician noted primarily for his contribution to the theory of stellar nucleosynthesis and his often controversial stance on other cosmological and scientific matters—in particular his rejection of the "Big Bang" theory, a term originally...
; Astronomy, A history of man's investigation of the universe
Recent
- Joseph Lindenberg; Universally Significant Numbers
- Bob Palais; Pi Is Wrong!
- Peter Harremoës; Al-Kashi’s constant
- Michael Hartl; The Tau Manifesto
- Following the tradition of Pi DayPi DayPi Day is a holiday commemorating the mathematical constant π . Pi Day is celebrated on March 14 , since 3, 1 and 4 are the three most significant digits of π in the decimal form...
(March 14, or 3.14), "2pi day" has been celebrated on June 28 (6.28), and became more widely adopted (as "tau day") since the publication of Hartl's manifesto in 2010. It has been argued that this is a "perfect day" because 6 and 28 are the two first perfect numbers.
Choice of a symbol
Many symbols have been suggested for the proposed circle constant, including:-
 as a single symbol, by LaurentPaul Matthieu Hermann LaurentPaul Matthieu Hermann Laurent was a French mathematician. Despite his large body of works, Laurent series expansions for complex functions were not named after him, but after Pierre Alphonse Laurent.-External links:...
as a single symbol, by LaurentPaul Matthieu Hermann LaurentPaul Matthieu Hermann Laurent was a French mathematician. Despite his large body of works, Laurent series expansions for complex functions were not named after him, but after Pierre Alphonse Laurent.-External links:...
in Traité D'Algebra -
 , by Lindenberg
, by Lindenberg -
 ("pi with 3 legs"), by Palais
("pi with 3 legs"), by Palais -
 or
or  (variant pi), by Harremoës
(variant pi), by Harremoës -
 , by Hartl (to stand for turnTurn (geometry)A turn is an angle equal to a 360° or 2 radians or \tau radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot....
, by Hartl (to stand for turnTurn (geometry)A turn is an angle equal to a 360° or 2 radians or \tau radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot....
or (tornos), since radianRadianRadian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s are equivalent to one full turnTurn (geometry)A turn is an angle equal to a 360° or 2 radians or \tau radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot....
).
Tau has become the most popular choice for the constant, but opponents argue that the letter has many other unrelated mathematical meanings. Supporters on the other hand state that precisely the fact that several meanings already coexist suggests that this is not problematic.
External links
Decimal expansion of 2*Pi and related links at the On-Line Encyclopedia of Integer SequencesOn-Line Encyclopedia of Integer Sequences
The On-Line Encyclopedia of Integer Sequences , also cited simply as Sloane's, is an online database of integer sequences, created and maintained by N. J. A. Sloane, a researcher at AT&T Labs...

