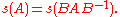Spread of a matrix
Encyclopedia
In matrix theory, the spread of a matrix describes how far apart the eigenvalues are in the complex plane
.
Suppose
is a square matrix with eigenvalues 
. Then the spread of 
is the non-negative number
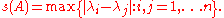
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
.
Suppose
is a square matrix with eigenvalues . Then the spread of is the non-negative number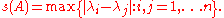Examples
- For the zero matrix and the identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
, the spread is zero. - Only
and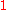 
can be eigenvalues for a projectionProjection (mathematics)Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
. A projection matrix therefore has spread
or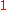 
. - All eigenvalues of an unitary matrix
lie on the unit circleUnit circleIn mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
. Hence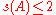
. - The spread of a matrix depends only on the spectrumSpectral theoryIn mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
of the matrix, so if
is invertible, then
