
Spearman's rank correlation coefficient
Encyclopedia
In statistics
, Spearman's rank correlation coefficient or Spearman's rho, named after Charles Spearman
and often denoted by the Greek letter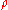
(rho) or as , is a non-parametric
, is a non-parametric
measure of statistical dependence between two variables. It assesses how well the relationship between two variables can be described using a monotonic function. If there are no repeated data values, a perfect Spearman correlation of +1 or −1 occurs when each of the variables is a perfect monotone function of the other.
variables. The n raw score
s are converted to ranks
are converted to ranks 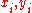 , and ρ is computed from these:
, and ρ is computed from these:
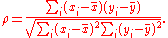
Tied values are assigned a rank equal to the average of their positions in the ascending order of the values. In the table below, notice how the rank of values that are the same is the mean of what their ranks would otherwise be:
In applications where ties are known to be absent, a simpler procedure can be used to calculate ρ. Differences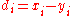 between the ranks of each observation on the two variables are calculated, and ρ is given by:
between the ranks of each observation on the two variables are calculated, and ρ is given by:

An alternative name for the Spearman rank correlation is the "grade correlation"; in this, the "rank" of an observation is replaced by the "grade". In continuous distributions, the grade of an observation is, by convention, always one half less than the rank, and hence the grade and rank correlations are the same in this case. More generally, the "grade" of an observation is proportional to an estimate of the fraction of a population less than a given value, with the half-observation adjustment at observed values. Thus this corresponds to one possible treatment of tied ranks. While unusual, the term "grade correlation" is still in use.
The Spearman correlation coefficient is often described as being "nonparametric." This can have two meanings. First, the fact that a perfect Spearman correlation results when X and Y are related by any monotonic function
can be contrasted with the Pearson correlation, which only gives a perfect value when X and Y are related by a linear function. The other sense in which the Spearman correlation is non-parametric in that its exact sampling distribution can be obtained without requiring knowledge of the joint probability distribution
of X and Y.
First, we must find the value of the term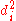 . To do so we use the following steps, reflected in the table below.
. To do so we use the following steps, reflected in the table below.
With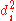 found, we can add them to find
found, we can add them to find 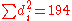 . The value of n is 10. So these values can now be substituted back into the equation,
. The value of n is 10. So these values can now be substituted back into the equation,

Which evaluates to ρ = −0.175757575...
With a P-value
= 0.6864058 (using the t distribution)
This low value shows that the correlation between IQ and hours spent watching TV is very low. In the case of ties in the original values, this formula should not be used. Instead, the Pearson correlation coefficient should be calculated on the ranks (where ties are given ranks, as described above).
, by using a permutation test. An advantage of this approach is that it automatically takes into account the number of tied data values there are in the sample, and the way they are treated in computing the rank correlation.
Another approach parallels the use of the Fisher transformation
in the case of the Pearson product-moment correlation coefficient. That is, confidence intervals and hypothesis tests relating to the population value ρ can be carried out using the Fisher transformation:
If F(r) is the Fisher transformation of r, the sample Spearman rank correlation coefficient, and n is the sample size, then

is a z-score
for r which approximately follows a standard normal distribution under the null hypothesis
of statistical independence
(ρ = 0).
One can also test for significance using

which is distributed approximately as Student's t distribution with n − 2 degrees of freedom under the null hypothesis
. A justification for this result relies on a permutation argument.
A generalization of the Spearman coefficient is useful in the situation where there are three or more conditions, a number of subjects are all observed in each of them, and it is predicted that the observations will have a particular order. For example, a number of subjects might each be given three trials at the same task, and it is predicted that performance will improve from trial to trial. A test of the significance of the trend between conditions in this situation was developed by E. B. Page and is usually referred to as Page's trend test
for ordered alternatives.
is a statistical method that gives a score to every value of two nominal variables. In this way the Pearson correlation coefficient
between them is maximized.
There exists an equivalent of this method, called grade correspondence analysis, which maximizes Spearman's rho or Kendall's tau.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, Spearman's rank correlation coefficient or Spearman's rho, named after Charles Spearman
Charles Spearman
Charles Edward Spearman, FRS was an English psychologist known for work in statistics, as a pioneer of factor analysis, and for Spearman's rank correlation coefficient...
and often denoted by the Greek letter
Rho (letter)
Rho is the 17th letter of the Greek alphabet. In the system of Greek numerals, it has a value of 100. It is derived from Semitic resh "head"...
(rho) or as
 , is a non-parametric
, is a non-parametricNon-parametric statistics
In statistics, the term non-parametric statistics has at least two different meanings:The first meaning of non-parametric covers techniques that do not rely on data belonging to any particular distribution. These include, among others:...
measure of statistical dependence between two variables. It assesses how well the relationship between two variables can be described using a monotonic function. If there are no repeated data values, a perfect Spearman correlation of +1 or −1 occurs when each of the variables is a perfect monotone function of the other.
Definition and calculation
The Spearman correlation coefficient is defined as the Pearson correlation coefficient between the rankedRanking
A ranking is a relationship between a set of items such that, for any two items, the first is either 'ranked higher than', 'ranked lower than' or 'ranked equal to' the second....
variables. The n raw score
Raw score
In statistics and data analysis, a raw score is an original datum that has not been transformed. This may include, for example, the original result obtained by a student on a test as opposed to that score after transformation to a standard score or percentile rank or the like.Often the conversion...
s
 are converted to ranks
are converted to ranks 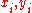 , and ρ is computed from these:
, and ρ is computed from these: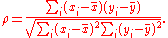
Tied values are assigned a rank equal to the average of their positions in the ascending order of the values. In the table below, notice how the rank of values that are the same is the mean of what their ranks would otherwise be:
Variable  | Position in the descending order | Rank  |
|---|---|---|
| 0.8 | 5 | 5 |
| 1.2 | 4 | 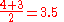 |
| 1.2 | 3 |  |
| 2.3 | 2 | 2 |
| 18 | 1 | 1 |
In applications where ties are known to be absent, a simpler procedure can be used to calculate ρ. Differences
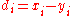 between the ranks of each observation on the two variables are calculated, and ρ is given by:
between the ranks of each observation on the two variables are calculated, and ρ is given by:
Related quantities
There are several other numerical measures that quantify the extent of statistical dependence between pairs of observations: these are discussed at correlation and dependence. The most common of these is the Pearson product moment correlation coefficient.An alternative name for the Spearman rank correlation is the "grade correlation"; in this, the "rank" of an observation is replaced by the "grade". In continuous distributions, the grade of an observation is, by convention, always one half less than the rank, and hence the grade and rank correlations are the same in this case. More generally, the "grade" of an observation is proportional to an estimate of the fraction of a population less than a given value, with the half-observation adjustment at observed values. Thus this corresponds to one possible treatment of tied ranks. While unusual, the term "grade correlation" is still in use.
Interpretation
The sign of the Spearman correlation indicates the direction of association between X (the independent variable) and Y (the dependent variable). If Y tends to increase when X increases, the Spearman correlation coefficient is positive. If Y tends to decrease when X increases, the Spearman correlation coefficient is negative. A Spearman correlation of zero indicates that there is no tendency for Y to either increase or decrease when X increases. The Spearman correlation increases in magnitude as X and Y become closer to being perfect monotone functions of each other. When X and Y are perfectly monotonically related, the Spearman correlation coefficient becomes 1. A perfect monotone increasing relationship implies that for any two pairs of data values Xi, Yi and Xj, Yj, that Xi − Xj and Yi − Yj always have the same sign. A perfect monotone decreasing relationship implies that these differences always have opposite signs.The Spearman correlation coefficient is often described as being "nonparametric." This can have two meanings. First, the fact that a perfect Spearman correlation results when X and Y are related by any monotonic function
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
can be contrasted with the Pearson correlation, which only gives a perfect value when X and Y are related by a linear function. The other sense in which the Spearman correlation is non-parametric in that its exact sampling distribution can be obtained without requiring knowledge of the joint probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of X and Y.
Example
In this example, we will use the raw data in the table below to calculate the correlation between the IQ of a person with the number of hours spent in front of TV per week.IQ,  |
Hours of TV per week,  |
| 106 | 7 |
| 86 | 0 |
| 100 | 27 |
| 101 | 50 |
| 99 | 28 |
| 103 | 29 |
| 97 | 20 |
| 113 | 12 |
| 112 | 6 |
| 110 | 17 |
First, we must find the value of the term
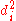 . To do so we use the following steps, reflected in the table below.
. To do so we use the following steps, reflected in the table below.
- Sort the data by the first column (
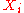 ). Create a new column
). Create a new column 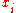 and assign it the ranked values 1,2,3,...n.
and assign it the ranked values 1,2,3,...n. - Next, sort the data by the second column (
 ). Create a fourth column
). Create a fourth column 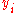 and similarly assign it the ranked values 1,2,3,...n.
and similarly assign it the ranked values 1,2,3,...n. - Create a fifth column
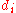 to hold the differences between the two rank columns (
to hold the differences between the two rank columns (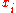 and
and 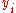 ).
). - Create one final column
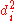 to hold the value of column
to hold the value of column 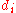 squared.
squared.
IQ, 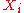 |
Hours of TV per week,  |
rank 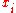 |
rank 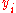 |
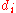 |
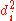 |
| 86 | 0 | 1 | 1 | 0 | 0 |
| 97 | 20 | 2 | 6 | −4 | 16 |
| 99 | 28 | 3 | 8 | −5 | 25 |
| 100 | 27 | 4 | 7 | −3 | 9 |
| 101 | 50 | 5 | 10 | −5 | 25 |
| 103 | 29 | 6 | 9 | −3 | 9 |
| 106 | 7 | 7 | 3 | 4 | 16 |
| 110 | 17 | 8 | 5 | 3 | 9 |
| 112 | 6 | 9 | 2 | 7 | 49 |
| 113 | 12 | 10 | 4 | 6 | 36 |
With
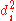 found, we can add them to find
found, we can add them to find 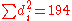 . The value of n is 10. So these values can now be substituted back into the equation,
. The value of n is 10. So these values can now be substituted back into the equation,
Which evaluates to ρ = −0.175757575...
With a P-value
P-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
= 0.6864058 (using the t distribution)
This low value shows that the correlation between IQ and hours spent watching TV is very low. In the case of ties in the original values, this formula should not be used. Instead, the Pearson correlation coefficient should be calculated on the ranks (where ties are given ranks, as described above).
Determining significance
One approach to testing whether an observed value of ρ is significantly different from zero (r will always maintain 1 ≥ r ≥ −1) is to calculate the probability that it would be greater than or equal to the observed r, given the null hypothesisNull hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
, by using a permutation test. An advantage of this approach is that it automatically takes into account the number of tied data values there are in the sample, and the way they are treated in computing the rank correlation.
Another approach parallels the use of the Fisher transformation
Fisher transformation
In statistics, hypotheses about the value of the population correlation coefficient ρ between variables X and Y can be tested using the Fisher transformation applied to the sample correlation coefficient r.-Definition:...
in the case of the Pearson product-moment correlation coefficient. That is, confidence intervals and hypothesis tests relating to the population value ρ can be carried out using the Fisher transformation:
If F(r) is the Fisher transformation of r, the sample Spearman rank correlation coefficient, and n is the sample size, then

is a z-score
Standard score
In statistics, a standard score indicates how many standard deviations an observation or datum is above or below the mean. It is a dimensionless quantity derived by subtracting the population mean from an individual raw score and then dividing the difference by the population standard deviation...
for r which approximately follows a standard normal distribution under the null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
of statistical independence
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
(ρ = 0).
One can also test for significance using

which is distributed approximately as Student's t distribution with n − 2 degrees of freedom under the null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
. A justification for this result relies on a permutation argument.
A generalization of the Spearman coefficient is useful in the situation where there are three or more conditions, a number of subjects are all observed in each of them, and it is predicted that the observations will have a particular order. For example, a number of subjects might each be given three trials at the same task, and it is predicted that performance will improve from trial to trial. A test of the significance of the trend between conditions in this situation was developed by E. B. Page and is usually referred to as Page's trend test
Page's trend test
In statistics, the Page test for multiple comparisons between ordered correlated variables is the counterpart of Spearman's rank correlation coefficient which summarizes the association of continuous variables. It is also known as Page's trend test or Page's L test...
for ordered alternatives.
Correspondence analysis based on Spearman's rho
Classic correspondence analysisCorrespondence analysis
Correspondence analysis is a multivariate statistical technique proposed by Hirschfeld and later developed by Jean-Paul Benzécri. It is conceptually similar to principal component analysis, but applies to categorical rather than continuous data...
is a statistical method that gives a score to every value of two nominal variables. In this way the Pearson correlation coefficient
Pearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
between them is maximized.
There exists an equivalent of this method, called grade correspondence analysis, which maximizes Spearman's rho or Kendall's tau.
See also
- Kendall tau rank correlation coefficientKendall tau rank correlation coefficientIn statistics, the Kendall rank correlation coefficient, commonly referred to as Kendall's tau coefficient, is a statistic used to measure the association between two measured quantities...
- Rank correlationRank correlationIn statistics, a rank correlation is the relationship between different rankings of the same set of items. A rank correlation coefficient measures the degree of similarity between two rankings, and can be used to assess its significance....
- Chebyshev's sum inequalityChebyshev's sum inequalityIn mathematics, Chebyshev's sum inequality, named after Pafnuty Chebyshev, states that ifa_1 \geq a_2 \geq \cdots \geq a_nandb_1 \geq b_2 \geq \cdots \geq b_n,then...
, rearrangement inequality (These two articles may shed light on the mathematical properties of Spearman's ρ.) - Pearson product-moment correlation coefficientPearson product-moment correlation coefficientIn statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
, a similar correlation method that measures the "linear" relationships between the raw numbers rather than between their ranks.
External links
- "Understanding Correlation vs. Copulas in Excel" by Eric Torkia, Technology Partnerz 2011
- Table of critical values of ρ for significance with small samples
- A calculator that shows the working out for Spearman's correlation
- Spearman's rank online calculator
- Chapter 3 part 1 shows the formula to be used when there are ties
- Spearman's rank correlation: Simple notes for students with an example of usage by biologists and a spreadsheet for Microsoft ExcelMicrosoft ExcelMicrosoft Excel is a proprietary commercial spreadsheet application written and distributed by Microsoft for Microsoft Windows and Mac OS X. It features calculation, graphing tools, pivot tables, and a macro programming language called Visual Basic for Applications...
for calculating it (a part of materials for a Research Methods in Biology course).


