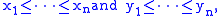Rearrangement inequality
Encyclopedia
In mathematics
, the rearrangement inequality states that

for every choice of real number
s
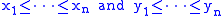
and every permutation

of x1, . . ., xn. If the numbers are different, meaning that
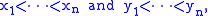
then the lower bound is attained only for the permutation which reverses the order, i.e. σ(i) = n − i + 1 for all i = 1, ..., n, and the upper bound is attained only for the identity, i.e. σ(i) = i for all i = 1, ..., n.
Note that the rearrangement inequality makes no assumptions on the signs of the real numbers.
we have
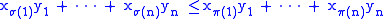
as soon as the permutation π has smaller number of inversions (i.e., such pairs of indices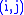 that
that  and
and  ) than the permutation
) than the permutation  .
.
Note that the identity permutation (1, 2, ..., n) has zero inversions while the permutation (n, n − 1, ..., 1) has the maximum possible number of inversions equal to n(n − 1)/2, implying the classic rearrangement inequality.
The original publication of the general rearrangement inequality claimed its correctness for all integers n ≥ 1, however for n ≥ 4 there exist counterexample
s.
, the Cauchy–Schwarz inequality
, and Chebyshev's sum inequality
.

Therefore, it suffices to prove the upper bound. Since there are only finitely many permutations, there exists at least one for which

is maximal. In case there are several permutations with this property, let σ denote one with the highest number of fixed points
.
We will now prove by contradiction
, that σ has to be the identity (then we are done). Assume that σ is not the identity. Then there exists a j in {1, ..., n − 1} such that σ(j) ≠ j and σ(i) = i for all i in {1, ..., j − 1}. Hence σ(j) > j and there exists k in {j + 1, ..., n} with σ(k) = j. Now
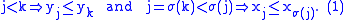
Therefore,

Expanding this product and rearranging gives
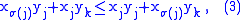
hence the permutation

which arises from σ by exchanging the values σ(j) and σ(k), has at least one additional fixed point compared to σ, namely at j, and also attains the maximum. This contradicts the choice of σ.
If
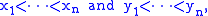
then we have strict inequalities at (1), (2), and (3), hence the maximum can only be attained by the identity, any other permutation σ cannot be optimal.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the rearrangement inequality states that

for every choice of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s
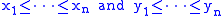
and every permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...

of x1, . . ., xn. If the numbers are different, meaning that
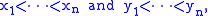
then the lower bound is attained only for the permutation which reverses the order, i.e. σ(i) = n − i + 1 for all i = 1, ..., n, and the upper bound is attained only for the identity, i.e. σ(i) = i for all i = 1, ..., n.
Note that the rearrangement inequality makes no assumptions on the signs of the real numbers.
General rearrangement inequality
For an integer n ≤ 3 and any two sets of real numberswe have
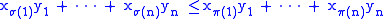
as soon as the permutation π has smaller number of inversions (i.e., such pairs of indices
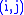 that
that  and
and  ) than the permutation
) than the permutation  .
.Note that the identity permutation (1, 2, ..., n) has zero inversions while the permutation (n, n − 1, ..., 1) has the maximum possible number of inversions equal to n(n − 1)/2, implying the classic rearrangement inequality.
The original publication of the general rearrangement inequality claimed its correctness for all integers n ≥ 1, however for n ≥ 4 there exist counterexample
Counterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
s.
Applications
Many famous inequalities can be proved by the rearrangement inequality, such as the arithmetic mean – geometric mean inequalityInequality of arithmetic and geometric means
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if...
, the Cauchy–Schwarz inequality
Cauchy–Schwarz inequality
In mathematics, the Cauchy–Schwarz inequality , is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, and other areas...
, and Chebyshev's sum inequality
Chebyshev's sum inequality
In mathematics, Chebyshev's sum inequality, named after Pafnuty Chebyshev, states that ifa_1 \geq a_2 \geq \cdots \geq a_nandb_1 \geq b_2 \geq \cdots \geq b_n,then...
.
Proof
The lower bound follows by applying the upper bound to
Therefore, it suffices to prove the upper bound. Since there are only finitely many permutations, there exists at least one for which

is maximal. In case there are several permutations with this property, let σ denote one with the highest number of fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
.
We will now prove by contradiction
Reductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
, that σ has to be the identity (then we are done). Assume that σ is not the identity. Then there exists a j in {1, ..., n − 1} such that σ(j) ≠ j and σ(i) = i for all i in {1, ..., j − 1}. Hence σ(j) > j and there exists k in {j + 1, ..., n} with σ(k) = j. Now
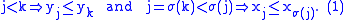
Therefore,

Expanding this product and rearranging gives
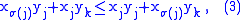
hence the permutation

which arises from σ by exchanging the values σ(j) and σ(k), has at least one additional fixed point compared to σ, namely at j, and also attains the maximum. This contradicts the choice of σ.
If
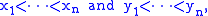
then we have strict inequalities at (1), (2), and (3), hence the maximum can only be attained by the identity, any other permutation σ cannot be optimal.