
Nilpotent Lie algebra
Encyclopedia
In mathematics
, a Lie algebra
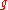 is nilpotent if the lower central series
is nilpotent if the lower central series
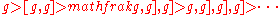
becomes zero eventually. Equivalently,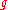 is nilpotent if
is nilpotent if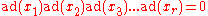
for any sequence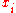 of elements of
of elements of  of sufficiently large length. (Here,
of sufficiently large length. (Here, 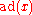 is given by
is given by  .) Consequences are that
.) Consequences are that 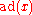 is nilpotent (as a linear map), and that the Killing form
is nilpotent (as a linear map), and that the Killing form
of a nilpotent Lie algebra is identically zero. (In comparison, a Lie algebra is semisimple if and only if its Killing form is nondegenerate.)
Every nilpotent Lie algebra is solvable; this fact gives one of the powerful ways to prove the solvability of a Lie algebra since, in practice, it is usually easier to prove the nilpotency than the solvability. The converse is not true in general. A Lie algebra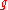 is nilpotent if and only if its quotient over an ideal containing the center of
is nilpotent if and only if its quotient over an ideal containing the center of 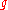 is nilpotent.
is nilpotent.
Most of classic classification results on nilpotency are concerned with finite-dimensional Lie algebras over a field of characteristic 0. Let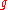 be a finite-dimensional Lie algebra.
be a finite-dimensional Lie algebra.  is nilpotent if and only if
is nilpotent if and only if 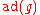 is nilpotent. Engel's theorem states that
is nilpotent. Engel's theorem states that 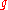 is nilpotent if and only if
is nilpotent if and only if 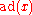 is nilpotent for every
is nilpotent for every 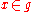 .
. 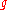 is solvable if and only if
is solvable if and only if 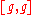 is nilpotent.
is nilpotent.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
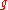 is nilpotent if the lower central series
is nilpotent if the lower central series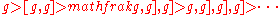
becomes zero eventually. Equivalently,
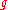 is nilpotent if
is nilpotent if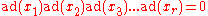
for any sequence
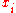 of elements of
of elements of  of sufficiently large length. (Here,
of sufficiently large length. (Here, 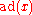 is given by
is given by  .) Consequences are that
.) Consequences are that 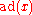 is nilpotent (as a linear map), and that the Killing form
is nilpotent (as a linear map), and that the Killing formKilling form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
of a nilpotent Lie algebra is identically zero. (In comparison, a Lie algebra is semisimple if and only if its Killing form is nondegenerate.)
Every nilpotent Lie algebra is solvable; this fact gives one of the powerful ways to prove the solvability of a Lie algebra since, in practice, it is usually easier to prove the nilpotency than the solvability. The converse is not true in general. A Lie algebra
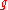 is nilpotent if and only if its quotient over an ideal containing the center of
is nilpotent if and only if its quotient over an ideal containing the center of 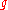 is nilpotent.
is nilpotent.Most of classic classification results on nilpotency are concerned with finite-dimensional Lie algebras over a field of characteristic 0. Let
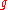 be a finite-dimensional Lie algebra.
be a finite-dimensional Lie algebra.  is nilpotent if and only if
is nilpotent if and only if 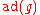 is nilpotent. Engel's theorem states that
is nilpotent. Engel's theorem states that 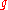 is nilpotent if and only if
is nilpotent if and only if 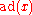 is nilpotent for every
is nilpotent for every 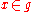 .
. 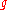 is solvable if and only if
is solvable if and only if 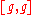 is nilpotent.
is nilpotent.Examples
- Every subalgebra and quotient of a nilpotent Lie algebra is nilpotent.
- If
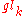 is the set of
is the set of  matrices, then the subalgebra consisting of strictly upper triangular matrices, denoted by
matrices, then the subalgebra consisting of strictly upper triangular matrices, denoted by 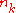 , is a nilpotent Lie algebra.
, is a nilpotent Lie algebra. - A Heisenberg algebra is nilpotent.
- A Cartan subalgebra of a Lie algebra is nilpotent and self-normalizing.

