
Uniform coloring
Encyclopedia
 111 |
 112 |
 123 |
|---|---|---|
| The hexagonal tiling has 3 uniform colorings. |
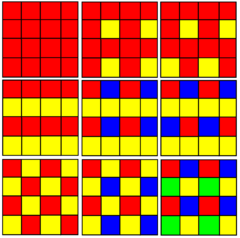
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a uniform coloring is a property of a uniform figure (uniform tiling
Uniform tiling
In geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-uniform.Uniform tilings can exist in both the Euclidean plane and hyperbolic plane...
or uniform polyhedron
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
) that is colored to be vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
. Different symmetries
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
can be expressed on the same geometric figure with the faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
following different uniform color patterns.
A uniform coloring can be specified by listing the different colors by indices around a vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
.
n-uniform figures
In addition, an n-uniform coloring is a property of a uniform figure which has n types vertex figureVertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
, that are collectively vertex transitive.

