Size functor
Encyclopedia
Given a size pair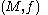 
where 
is a manifold
of dimension
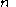and 
is an arbitrary real continuous function
defined
on it, the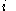
-th size functor, with 
, denoted
by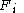
, is the functor
in
, where 
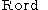is the category
of ordered real numbers, and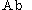
is the category
of Abelian groups, defined in the following way. For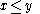
, setting 
, 
, 
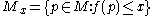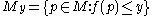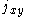equal to the inclusion from 
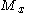into 
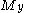, and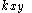 
equal to the morphism
in
from 
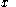to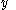 
,
In other words, the size functor studies the
process of the birth and death of homology classes as the lower level set changes.
When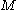
is smooth and compact and 
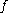is a Morse function, the functor 
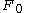can be
described by oriented trees, called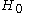
− trees.
The concept of size functor was introduced as an extension to homology theory
and category theory
of the idea of size function
. The main motivation for introducing the size functor originated by the observation that the size function
can be seen as the rank
of the image of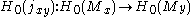
.
The concept of size functor is strictly related to the concept of persistent homology group
,
studied in persistent homology. It is worth to point out that the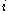
-th persistent homology group coincides with the image of the homomorphism
.
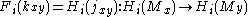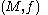where is a manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
of dimension
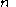and is an arbitrary real continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
defined
on it, the
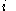-th size functor, with , denotedby
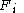, is the functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
in
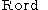, where is the categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of ordered real numbers, and
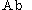is the categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of Abelian groups, defined in the following way. For
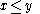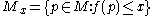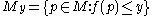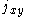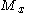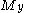, setting , , equal to the inclusion from into , and 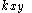equal to the morphismMorphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
in
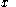from to 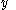,- for each
, 
-
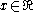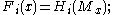
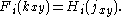
In other words, the size functor studies the
process of the birth and death of homology classes as the lower level set changes.
When
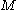is smooth and compact and 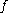is a Morse function, the functor 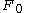can bedescribed by oriented trees, called
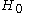− trees.The concept of size functor was introduced as an extension to homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
and category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
of the idea of size function
Size function
Size functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane xSize functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane...
. The main motivation for introducing the size functor originated by the observation that the size function
Size function
Size functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane xSize functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane...
can be seen as the rankof the image of
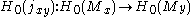.The concept of size functor is strictly related to the concept of persistent homology group
,
studied in persistent homology. It is worth to point out that the
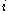-th persistent homology group coincides with the image of the homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
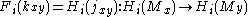.See also
- Size theory
- Size functionSize functionSize functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane xSize functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane...
- Size homotopy group
- Size pair