Singular cardinal hypothesis
Encyclopedia
In set theory
, the singular cardinals hypothesis (SCH) arose from the question of whether the least cardinal number
for which the generalized continuum hypothesis (GCH) might fail could be a singular cardinal.
According to Mitchell (1992), the singular cardinals hypothesis is:
Here, κ+ denotes the successor cardinal
of κ.
Since SCH is a consequence of GCH which is known to be consistent with ZFC
, SCH is consistent with ZFC. The negation of SCH has also been shown to be consistent with ZFC, if one assumes the existence of a sufficiently large cardinal number. In fact, by results of Moti Gitik
, ZFC + the negation of SCH is equiconsistent with ZFC + the existence of a measurable cardinal
of Mitchell order
.
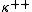Another form of the SCH is the following statement:
where cf denotes the cofinality
function. Since whenever
is a singular strong limit cardinal,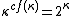 
, this formulation is equivalent (over ZFC) to the formulation given above.
Silver
proved that if κ is singular with uncountable cofinality and 2λ = λ+ for all infinite cardinals λ < κ, then 2κ = κ+. Silver's original proof used generic ultrapowers. The following important fact follows from Silver's theorem: if the singular cardinals hypothesis holds for all singular cardinals of countable cofinality, then it holds for all singular cardinals. In particular, then, if
is the least counterexample to the singular cardinals hypothesis, then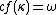 
.
The negation of the singular cardinals hypothesis is intimately related to violating the GCH at a measurable cardinal. A well-known result of Dana Scott
is that if the GCH holds below a measurable cardinal
on a set of measure one--i.e., there is normal 
-complete ultrafilter D on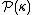 
such that 
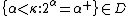, then 
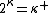. Starting with 
a supercompact cardinal, Silver was able to produce a model of set theory in which 
is measurable and in which 
. Then, by applying Prikry forcing to the measurable 
, one gets a model of set theory in which 
is a strong limit cardinal of countable cofinality and in which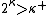 
--a violation of the SCH. Gitik
, building on work of Woodin
, was able to replace the supercompact in Silver's proof with a measurable of Mitchell order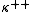
. That established an upper bound for the consistency strength of the failure of the SCH. Gitik again, using results of Inner model theory
, was able to show that a measurable of Mitchell order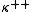
is also the lower bound for the consistency strength of the failure of SCH.
A wide variety of propositions imply SCH. As was noted above, GCH implies SCH. On the other hand, the proper forcing axiom
which implies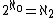
and hence is incompatible with GCH also implies SCH. Solovay
showed that large cardinals almost imply SCH--in particular, if
is strongly compact cardinal
, then the SCH holds above
. On the other hand, the non-existence of (inner models for) various large cardinals (below a measurable of Mitchell order 
) also imply SCH.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, the singular cardinals hypothesis (SCH) arose from the question of whether the least cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
for which the generalized continuum hypothesis (GCH) might fail could be a singular cardinal.
According to Mitchell (1992), the singular cardinals hypothesis is:
- If κ is any singular strong limit cardinalLimit cardinalIn mathematics, limit cardinals are certain cardinal numbers. A cardinal number λ is a weak limit cardinal if λ is neither a successor cardinal nor zero. This means that one cannot "reach" λ by repeated successor operations...
, then 2κ = κ+.
Here, κ+ denotes the successor cardinal
Successor cardinal
In the theory of cardinal numbers, we can define a successor operation similar to that in the ordinal numbers. This coincides with the ordinal successor operation for finite cardinals, but in the infinite case they diverge because every infinite ordinal and its successor have the same cardinality...
of κ.
Since SCH is a consequence of GCH which is known to be consistent with ZFC
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
, SCH is consistent with ZFC. The negation of SCH has also been shown to be consistent with ZFC, if one assumes the existence of a sufficiently large cardinal number. In fact, by results of Moti Gitik
Moti Gitik
Moti Gitik is a mathematician, working in set theory. Gitik is professor at the Tel-Aviv University. He proved the consistency of "all uncountable cardinals are singular" from the consistency of "there is a proper class of strongly compact cardinals"...
, ZFC + the negation of SCH is equiconsistent with ZFC + the existence of a measurable cardinal
of Mitchell orderMitchell order
In mathematical set theory, the Mitchell order is a well-founded preorder on the set of normal measures on a measurable cardinal κ. It is named for William Mitchell. We say that M ◅ N if M is in the ultrapower model defined by N...
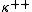.Another form of the SCH is the following statement:
- 2cf(κ) < κ implies κcf(κ) = κ+,
where cf denotes the cofinality
Cofinality
In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
function. Since whenever
is a singular strong limit cardinal, 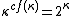, this formulation is equivalent (over ZFC) to the formulation given above.Silver
Jack Silver
Jack Howard Silver is a set theorist and logician at the University of California, Berkeley. He has made several deep contributions to set theory...
proved that if κ is singular with uncountable cofinality and 2λ = λ+ for all infinite cardinals λ < κ, then 2κ = κ+. Silver's original proof used generic ultrapowers. The following important fact follows from Silver's theorem: if the singular cardinals hypothesis holds for all singular cardinals of countable cofinality, then it holds for all singular cardinals. In particular, then, if
is the least counterexample to the singular cardinals hypothesis, then 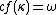.The negation of the singular cardinals hypothesis is intimately related to violating the GCH at a measurable cardinal. A well-known result of Dana Scott
Dana Scott
Dana Stewart Scott is the emeritus Hillman University Professor of Computer Science, Philosophy, and Mathematical Logic at Carnegie Mellon University; he is now retired and lives in Berkeley, California...
is that if the GCH holds below a measurable cardinal
on a set of measure one--i.e., there is normal -complete ultrafilter D on 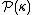such that 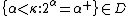, then 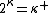. Starting with a supercompact cardinal, Silver was able to produce a model of set theory in which is measurable and in which . Then, by applying Prikry forcing to the measurable , one gets a model of set theory in which is a strong limit cardinal of countable cofinality and in which 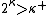--a violation of the SCH. GitikMoti Gitik
Moti Gitik is a mathematician, working in set theory. Gitik is professor at the Tel-Aviv University. He proved the consistency of "all uncountable cardinals are singular" from the consistency of "there is a proper class of strongly compact cardinals"...
, building on work of Woodin
W. Hugh Woodin
William Hugh Woodin is an American mathematician and set theorist at University of California, Berkeley. He has made many notable contributions to the theory of inner models and determinacy. A type of large cardinal, the Woodin cardinal, bears his name.-Biography:Born in Tucson, Arizona, Woodin...
, was able to replace the supercompact in Silver's proof with a measurable of Mitchell order
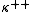. That established an upper bound for the consistency strength of the failure of the SCH. Gitik again, using results of Inner model theoryInner model theory
In set theory, inner model theory is the study of certain models of ZFC or some fragment or strengthening thereof. Ordinarily these models are transitive subsets or subclasses of the von Neumann universe V, or sometimes of a generic extension of V. Inner model theory studies the relationships of...
, was able to show that a measurable of Mitchell order
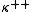is also the lower bound for the consistency strength of the failure of SCH.A wide variety of propositions imply SCH. As was noted above, GCH implies SCH. On the other hand, the proper forcing axiom
Proper Forcing Axiom
In the mathematical field of set theory, the proper forcing axiom is a significant strengthening of Martin's axiom, where forcings with the countable chain condition are replaced by proper forcings.- Statement :...
which implies
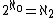and hence is incompatible with GCH also implies SCH. SolovayRobert M. Solovay
Robert Martin Solovay is an American mathematician specializing in set theory.Solovay earned his Ph.D. from the University of Chicago in 1964 under the direction of Saunders Mac Lane, with a dissertation on A Functorial Form of the Differentiable Riemann–Roch theorem...
showed that large cardinals almost imply SCH--in particular, if
is strongly compact cardinalStrongly compact cardinal
In mathematical set theory, a strongly compact cardinal is a certain kind of large cardinal number; their existence can neither be proven nor disproven from the standard axioms of set theory....
, then the SCH holds above
. On the other hand, the non-existence of (inner models for) various large cardinals (below a measurable of Mitchell order ) also imply SCH.