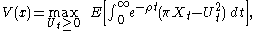Sethi model
Encyclopedia
The Sethi model was developed by Suresh P. Sethi
and describes the process of how sales evolve over time in response to advertising
. The rate of change in sales depend on three effects: response to advertising that acts positively on the unsold portion of the market, the loss due to forgetting or possibly due to competitive factors that act negatively on the sold portion of the market, and a random effect that can go either way.
Suresh Sethi published his paper "Deterministic and Stochastic Optimization of a Dynamic Advertising Model" in 1983. The Sethi model is a modification as well as a stochastic extension of the Vidale-Wolfe advertising model. The model and its competitive extensions have been used extensively in the literature. Moreover, some of these extensions have been also tested empirically.
:
Where:
 , the loss due to forgetting or possibly due to competitive factors that act negatively on the sold portion of the market via
, the loss due to forgetting or possibly due to competitive factors that act negatively on the sold portion of the market via 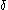 , and a random effect using a diffusion or White noise term that can go either way.
, and a random effect using a diffusion or White noise term that can go either way.
 , consider the following objective function:
, consider the following objective function:
where denotes the sales revenue corresponding to the total market, i.e., when
denotes the sales revenue corresponding to the total market, i.e., when  , and
, and 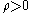 denotes the discount rate.
denotes the discount rate.
The function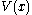 is known as the value function for this problem, and it is shown to be
is known as the value function for this problem, and it is shown to be
Suresh P. Sethi
Suresh P. Sethi is Charles & Nancy Davidson Distinguished Professor of Operations Management and Director of the Center for Intelligent Supply Networks at The University of Texas at Dallas. He has contributed significantly in the fields of manufacturing and operations management, finance and...
and describes the process of how sales evolve over time in response to advertising
Advertising
Advertising is a form of communication used to persuade an audience to take some action with respect to products, ideas, or services. Most commonly, the desired result is to drive consumer behavior with respect to a commercial offering, although political and ideological advertising is also common...
. The rate of change in sales depend on three effects: response to advertising that acts positively on the unsold portion of the market, the loss due to forgetting or possibly due to competitive factors that act negatively on the sold portion of the market, and a random effect that can go either way.
Suresh Sethi published his paper "Deterministic and Stochastic Optimization of a Dynamic Advertising Model" in 1983. The Sethi model is a modification as well as a stochastic extension of the Vidale-Wolfe advertising model. The model and its competitive extensions have been used extensively in the literature. Moreover, some of these extensions have been also tested empirically.
Model
The Sethi advertising model or simply the Sethi model provides a sales-advertising dynamics in the form of the following stochastic differential equationStochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
:
-
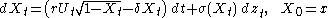 .
.
Where:
-
 is the market share at time
is the market share at time 
-
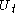 is the rate of advertising at time
is the rate of advertising at time 
-
 is the coefficient of the effectiveness of advertising
is the coefficient of the effectiveness of advertising -
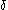 is the decay constant
is the decay constant -
 is the diffusion coefficient
is the diffusion coefficient -
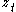 is the Wiener processWiener processIn mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
is the Wiener processWiener processIn mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
(Standard Brownian motionBrownian motionBrownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
);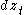 is known as White noiseWhite noiseWhite noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
is known as White noiseWhite noiseWhite noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
.
Explanation
The rate of change in sales depend on three effects: response to advertising that acts positively on the unsold portion of the market via , the loss due to forgetting or possibly due to competitive factors that act negatively on the sold portion of the market via
, the loss due to forgetting or possibly due to competitive factors that act negatively on the sold portion of the market via 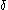 , and a random effect using a diffusion or White noise term that can go either way.
, and a random effect using a diffusion or White noise term that can go either way.- The coefficient
 is the coefficient of the effectiveness of advertising innovation.
is the coefficient of the effectiveness of advertising innovation. - The coefficient
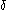 is the decay constant.
is the decay constant. - The square-root term brings in the so-called word-of-mouth effect at least at low sales levels.
- The diffusion term
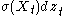 brings in the random effect.
brings in the random effect.
Example of an optimal advertising problem
Subject to the Sethi model above with the initial marke share , consider the following objective function:
, consider the following objective function:where
 denotes the sales revenue corresponding to the total market, i.e., when
denotes the sales revenue corresponding to the total market, i.e., when  , and
, and 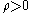 denotes the discount rate.
denotes the discount rate.The function
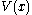 is known as the value function for this problem, and it is shown to be
is known as the value function for this problem, and it is shown to be-
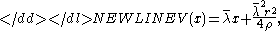
where
-

The optimal controlOptimal controlOptimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
for this problem is
-
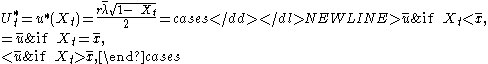
where
-
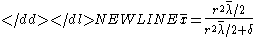
and
-

Extensions of the Sethi model
- Competitive extensions-Nash differential games
- Empirical testing of the Sethi model and extensions
- Stackelberg differential games
- The Sethi durable goods model
See also
- Bass diffusion modelBass diffusion modelrightThe Bass diffusion model was developed by Frank Bass and describes the process of how new products get adopted as an interaction between users and potential users. It has been described as one of the most famous empirical generalisations in marketing, along with the Dirichlet model of repeat...
- differential gameDifferential gameIn game theory, differential games are a group of problems related to the modeling and analysis of conflict in the context of a dynamical system. The problem usually consists of two actors, a pursuer and an evader, with conflicting goals...
s - Stochastic differential equationStochastic differential equationA stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
- Diffusion of innovationsDiffusion of innovationsDiffusion of Innovations is a theory that seeks to explain how, why, and at what rate new ideas and technology spread through cultures. Everett Rogers, a professor of rural sociology, popularized the theory in his 1962 book Diffusion of Innovations...
- Stackleberg competition
- Nash equilibriumNash equilibriumIn game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
-
-
-
-