The Bass diffusion model was developed by Frank Bass

Frank Bass

Frank M. Bass was an American academic in the field of marketing research, and is considered to be among the founders of marketing science. He was the creator of the Bass diffusion model that describes the adoption of new products and technologies by first-time buyers...

 and describes the process of how new products get adopted as an interaction between users and potential users. It has been described as one of the most famous empirical generalisations in marketing, along with the Dirichlet model of repeat buying and brand choice. The model is widely used in forecasting

Forecasting

Forecasting is the process of making statements about events whose actual outcomes have not yet been observed. A commonplace example might be estimation for some variable of interest at some specified future date. Prediction is a similar, but more general term...

, especially product forecasting

Product forecasting

Product forecasting is the science of predicting the degree of success a new product will enjoy in the marketplace. To do this, the forecasting model must take into account such things as product awareness, distribution, price, fulfilling unmeet needs and competitive alternatives.-Bass model:Bass...

 and technology forecasting

Technology forecasting

Technology forecasting attempts to predict the future characteristics of useful technological machines, procedures or techniques.-Important aspects:...

. Mathematically, the basic Bass diffusion is a Riccati equation

Riccati equation

In mathematics, a Riccati equation is any ordinary differential equation that is quadratic in the unknown function. In other words, it is an equation of the form y' = q_0 + q_1 \, y + q_2 \, y^2...

 with constant coefficients.

Frank Bass published his paper "A new product growth model for consumer durables" in 1969. Prior to this, Everett Rogers

Everett Rogers

Everett M. Rogers was a communication scholar, sociologist, writer, and teacher. He is best known for originating the diffusion of innovations theory and for introducing the term early adopter....

 published Diffusion of Innovations, a highly influential work that described the different stages of product adoption. Bass contributed some mathematical ideas to the concept.

This model has been widely influential in marketing and management science. In 2004 it was selected as one of the ten most frequently cited papers in the 50-year history of Management Science. It was ranked number five, and the only marketing paper in the list. It was subsequently reprinted in the December 2004 issue of Management Science.

Model formulation

Where:

• is the rate of change of the installed base fraction
• is the installed base fraction
• is the coefficient of innovation
• is the coefficient of imitation

Sales is the rate of change of installed base (i.e. adoption) multiplied by the ultimate market potential :


The time of peak sales

Explanation

The coefficient p is called the coefficient of innovation, external influence or advertising effect. The coefficient q is called the coefficient of imitation, internal influence or word-of-mouth effect.

Typical values of p and q when time t is measured in years:

• The average value of p has been found to be 0.03, and is often less than 0.01
• The average value of q has been found to be 0.38, with a typical range between 0.3 and 0.5

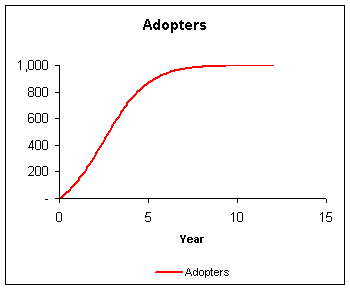
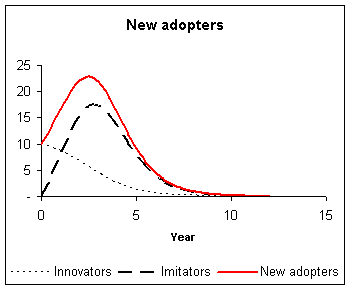
Generalised Bass model (with pricing)

Bass found that his model fit the data for almost all product introductions, despite a wide range of managerial decision variable, e.g. pricing and advertising. This means that decision variable can shift the Bass curve in time, but that the shape of the curve is always similar.

Although many extensions of the model have been proposed, only one of these reduces to the Bass model under ordinary circumstances. This model was developed in 1994 by Frank Bass, Trichy Krishnan and Dipak Jain:


where is a function of percentage change in price and other variables

Successive generations

Technology products succeed one another in generations. Norton and Bass extended the model in 1987 for sales of products with continuous repeat purchasing. The formulation for three generations is as follows:

where

• 
• is the incremental number of ultimate adopters of the ith generation product
• is the average (continuous) repeat buying rate among adopters of the ith generation product
• is the time since the introduction of the ith generation product
• 

It has been found that the p and q terms are generally the same between successive generations.

Relationship with other s-curves

There are two special cases of the Bass diffusion model.

• The first special case occurs when q=0, when the model reduces to the Exponential distribution
  Exponential distribution
  In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
  
  .
• The second special case reduces to the logistic distribution, when p=0.

The Bass model is a special case of the Gamma/shifted Gompertz distribution (G/SG).

Use in online social networks
The rapid, recent (as of early 2007) growth in online social networks (and other virtual communities) has led to an increased use of the Bass diffusion model. The Bass diffusion model is used to estimate the size and growth rate of these social networks.

External links

• Frank M. Bass Official Website