Quadratic differential
Encyclopedia
In mathematics
, a quadratic differential on a Riemann surface
is a section of the symmetric square of the holomorphic cotangent bundle
.
If the section is holomorphic, then the quadratic differential
is said to be holomorphic. The vector space of holomorphic quadratic differentials on a Riemann surface
has a natural interpretation as the cotangent space to the Riemann moduli space or Teichmueller space.
in the complex plane
may be written as
where 
is the complex variable and
is a complex valued function on 
.
Such a `local' quadratic differential is holomorphic if and only if
is holomorphic.
Given a chart
for a general Riemann surface 
and a quadratic differential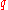
on 
, the pull-back
defines a quadratic differential on a domain in the complex plane.
is an abelian differential on a Riemann surface,
then
is a quadratic differential.
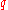determines a Riemannian metric 
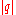on
the complement of its zeroes. If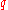
is defined on a domain in the complex plane
and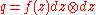
, then the associated Riemannian metric is
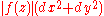where 
.
Since
is holomorphic, the curvature
of this metric is zero. Thus,
a holomorphic quadratic differential defines a flat metric on the complement of the
set of
such that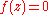 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a quadratic differential on a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
is a section of the symmetric square of the holomorphic cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
.
If the section is holomorphic, then the quadratic differential
is said to be holomorphic. The vector space of holomorphic quadratic differentials on a Riemann surface
has a natural interpretation as the cotangent space to the Riemann moduli space or Teichmueller space.
Local form
Each quadratic differential on a domain in the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
may be written as
where is the complex variable and is a complex valued function on .Such a `local' quadratic differential is holomorphic if and only if
is holomorphic.Given a chart
for a general Riemann surface and a quadratic differential
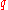on , the pull-back defines a quadratic differential on a domain in the complex plane.Relation to abelian differentials
If is an abelian differential on a Riemann surface,then
is a quadratic differential. Singular Euclidean structure
A holomorphic quadratic differential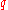 determines a Riemannian metric 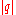onthe complement of its zeroes. If
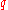is defined on a domain in the complex planeand
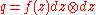, then the associated Riemannian metric is 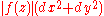where .Since
is holomorphic, the curvatureCurvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of this metric is zero. Thus,
a holomorphic quadratic differential defines a flat metric on the complement of the
set of
such that 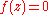.