
Sequential space
Encyclopedia
In topology
and related fields of mathematics
, a sequential space is a topological space
that satisfies a very weak axiom of countability
. Sequential spaces are the most general class of spaces for which sequence
s suffice to determine the topology.
Every sequential space has countable tightness.
The complement
of a sequentially open set is a sequentially closed set, and vice-versa. Every open subset of X is sequentially open and every closed set is sequentially closed. The converses are not generally true.
A sequential space is a space X satisfying one of the following equivalent conditions:
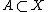 of a space
of a space 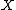 , the sequential closure
, the sequential closure 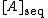 is the set
is the set
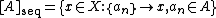
that is, the set of all points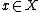 for which there is a sequence in
for which there is a sequence in 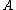 that converges to
that converges to  . The map
. The map
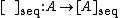
is called the sequential closure operator. It shares some properties with ordinary closure, in that the empty set is sequentially closed:
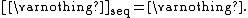
Every closed set is sequentially closed:
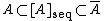
for all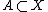 ; here
; here 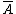 denotes the ordinary closure of the set
denotes the ordinary closure of the set 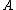 . Sequential closure commutes with union:
. Sequential closure commutes with union:
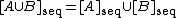
for all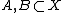 . However, unlike ordinary closure, the sequential closure operator is not in general idempotent; that is, one may have that
. However, unlike ordinary closure, the sequential closure operator is not in general idempotent; that is, one may have that
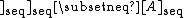
even when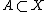 is a subset of a sequential space
is a subset of a sequential space 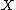 .
.
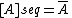
for all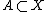 . A space is a Fréchet–Urysohn space if and only if every subspace is a sequential space. Every first-countable space
. A space is a Fréchet–Urysohn space if and only if every subspace is a sequential space. Every first-countable space
is a Fréchet–Urysohn space.
The space is named after Maurice Fréchet and Pavel Urysohn.
can be specified completely by the knowledge of its convergent sequences, and then he abstracted properties of first countable spaces that allowed this to be true.
is sequential, hence each second countable, metric space
, and discrete space
is sequential. Further examples are furnished by applying the categorical properties listed below. For example, every CW-complex is sequential, as it can be considered as a quotient of a metric space.
There are sequential spaces that are not first countable. (One example is to take the real line R and identify
the set Z of integers to a point.)
An example of a space that is not sequential is the cocountable topology
on an uncountable set. Every convergent sequence in such a space is eventually constant, hence every set is sequentially open. But the cocountable topology is not discrete
. In fact, one could say that the cocountable topology on an uncountable set is "sequentially discrete".
The final equivalent condition shows that the class of sequential spaces consists precisely of those spaces whose topological structure is determined by convergent sequences in the space.
The category Seq is not closed under the following operations in Top:
Since they are closed under topological sums and quotients, the sequential spaces form a coreflective subcategory of the category of topological spaces
. In fact, they are the coreflective hull of metrizable spaces (i.e., the smallest class of topological spaces closed under sums and quotients and containing the metrizable spaces).
The subcategory Seq is a cartesian closed category
with respect to its own product (not that of Top). The exponential object
s are equipped with the (convergent sequence)-open topology. P.I. Booth and A. Tillotson have shown that Seq is the smallest cartesian closed subcategory of Top containing the underlying topological spaces of all metric space
s, CW-complexes, and differentiable manifold
s and that is closed under colimits, quotients, and other "certain reasonable identities" that Norman Steenrod
described as "convenient".
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and related fields of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a sequential space is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
that satisfies a very weak axiom of countability
Axiom of countability
In mathematics, an axiom of countability is a property of certain mathematical objects that requires the existence of a countable set with certain properties, while without it such sets might not exist....
. Sequential spaces are the most general class of spaces for which sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s suffice to determine the topology.
Every sequential space has countable tightness.
Definitions
Let X be a topological space.- A subset U of X is sequentially open if each sequence (xn) in X converging to a point of U is eventually in U (i.e. there exists N such that xn is in U for all n ≥ N.)
- A subset F of X is sequentially closed if, whenever (xn) is a sequence in F converging to x, then x must also be in F.
The complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of a sequentially open set is a sequentially closed set, and vice-versa. Every open subset of X is sequentially open and every closed set is sequentially closed. The converses are not generally true.
A sequential space is a space X satisfying one of the following equivalent conditions:
- Every sequentially open subset of X is open.
- Every sequentially closed subset of X is closed.
Sequential closure
Given a subset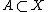 of a space
of a space 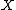 , the sequential closure
, the sequential closure 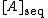 is the set
is the set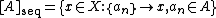
that is, the set of all points
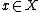 for which there is a sequence in
for which there is a sequence in 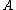 that converges to
that converges to  . The map
. The map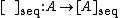
is called the sequential closure operator. It shares some properties with ordinary closure, in that the empty set is sequentially closed:
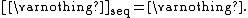
Every closed set is sequentially closed:
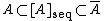
for all
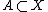 ; here
; here 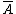 denotes the ordinary closure of the set
denotes the ordinary closure of the set 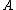 . Sequential closure commutes with union:
. Sequential closure commutes with union: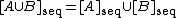
for all
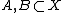 . However, unlike ordinary closure, the sequential closure operator is not in general idempotent; that is, one may have that
. However, unlike ordinary closure, the sequential closure operator is not in general idempotent; that is, one may have that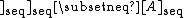
even when
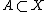 is a subset of a sequential space
is a subset of a sequential space 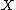 .
.Fréchet–Urysohn space
Topological spaces for which sequential closure is the same as ordinary closure are known as Fréchet–Urysohn spaces. That is, a Fréchet–Urysohn space has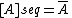
for all
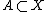 . A space is a Fréchet–Urysohn space if and only if every subspace is a sequential space. Every first-countable space
. A space is a Fréchet–Urysohn space if and only if every subspace is a sequential space. Every first-countable spaceFirst-countable space
In topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis...
is a Fréchet–Urysohn space.
The space is named after Maurice Fréchet and Pavel Urysohn.
History
Although spaces satisfying such properties had implicitly been studied for several years, the first formal definition is originally due to S. P. Franklin in 1965, who was investigating the question of "what are the classes of topological spaces that can be specified completely by the knowledge of their convergent sequences?" Franklin arrived at the definition above by noting that every first-countable spaceFirst-countable space
In topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis...
can be specified completely by the knowledge of its convergent sequences, and then he abstracted properties of first countable spaces that allowed this to be true.
Examples
Every first-countable spaceFirst-countable space
In topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis...
is sequential, hence each second countable, metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, and discrete space
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
is sequential. Further examples are furnished by applying the categorical properties listed below. For example, every CW-complex is sequential, as it can be considered as a quotient of a metric space.
There are sequential spaces that are not first countable. (One example is to take the real line R and identify
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
the set Z of integers to a point.)
An example of a space that is not sequential is the cocountable topology
Cocountable topology
The cocountable topology or countable complement topology on any set X consists of the empty set and all cocountable subsets of X, that is all sets whose complement in X is countable...
on an uncountable set. Every convergent sequence in such a space is eventually constant, hence every set is sequentially open. But the cocountable topology is not discrete
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
. In fact, one could say that the cocountable topology on an uncountable set is "sequentially discrete".
Equivalent conditions
Many conditions have been shown to be equivalent to X being sequential. Here are a few:- X is the quotient of a first countable space.
- X is the quotient of a metric space.
- For every topological space Y and every map f : X → Y, we have that f is continuous if and only if for every sequence of points (xn) in X converging to x, we have (f(xn)) converging to f(x).
The final equivalent condition shows that the class of sequential spaces consists precisely of those spaces whose topological structure is determined by convergent sequences in the space.
Categorical properties
The full subcategory Seq of all sequential spaces is closed under the following operations in Top:- Quotients
- Continuous closed or open images
- Sums
- Inductive limits
- Open and closed subspaces
The category Seq is not closed under the following operations in Top:
- Continuous images
- Subspaces
- Products
Since they are closed under topological sums and quotients, the sequential spaces form a coreflective subcategory of the category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
. In fact, they are the coreflective hull of metrizable spaces (i.e., the smallest class of topological spaces closed under sums and quotients and containing the metrizable spaces).
The subcategory Seq is a cartesian closed category
Cartesian closed category
In category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
with respect to its own product (not that of Top). The exponential object
Exponential object
In mathematics, specifically in category theory, an exponential object is the categorical equivalent of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories...
s are equipped with the (convergent sequence)-open topology. P.I. Booth and A. Tillotson have shown that Seq is the smallest cartesian closed subcategory of Top containing the underlying topological spaces of all metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s, CW-complexes, and differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
s and that is closed under colimits, quotients, and other "certain reasonable identities" that Norman Steenrod
Norman Steenrod
Norman Earl Steenrod was a preeminent mathematician most widely known for his contributions to the field of algebraic topology.-Life:...
described as "convenient".

