
Sequential probability ratio test
Encyclopedia
The sequential probability ratio test (SPRT) is a specific sequential hypothesis test
, developed by Abraham Wald
. Neyman and Pearson's 1933 result inspired Wald to reformulate it as a sequential analysis problem. The Neyman-Pearson lemma, by contrast, offers a rule of thumb
for when all the data is collected (and its likelihood ratio known).
While originally developed for use in quality control
studies in the realm of manufacturing, SPRT has been formulated for use in the computerized testing of human examinees as a termination criterion.
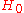 and
and 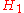 for the null hypothesis
for the null hypothesis
and alternative hypothesis respectively. They must be specified as follows:
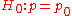
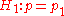
The next step is calculate the cumulative sum of the log-likelihood ratio, , as new data arrive:
, as new data arrive:

The stopping rule
is a simple thresholding scheme:
where a and b ( ) depend on the desired type I and type II errors
) depend on the desired type I and type II errors
, and
and 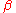 . They may be chosen as follows:
. They may be chosen as follows:
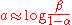 and
and 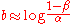
In other words, and
and 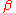 must be decided beforehand in order to set the thresholds appropriately. The numerical value will depend on the application. The reason for using approximation signs is that, in the discrete case, the signal may cross the threshold between samples. Thus, depending on the penalty of making an error and the sampling frequency, one might set the thresholds more aggressively. Of course, the exact bounds may be used in the continuous case.
must be decided beforehand in order to set the thresholds appropriately. The numerical value will depend on the application. The reason for using approximation signs is that, in the discrete case, the signal may cross the threshold between samples. Thus, depending on the penalty of making an error and the sampling frequency, one might set the thresholds more aggressively. Of course, the exact bounds may be used in the continuous case.
. Let us consider the exponential distribution
:

The hypotheses are simply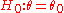 and
and 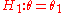 , with
, with  . Then the log-likelihood function (LLF) for one sample is
. Then the log-likelihood function (LLF) for one sample is
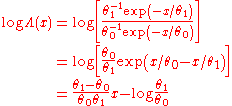
The cumulative sum of the LLFs for all x is
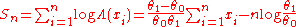
Accordingly, the stopping rule
is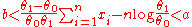
After re-arranging we finally find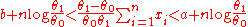
The thresholds are simply two parallel lines
with slope
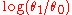 . Sampling should stop when the sum of the samples makes an excursion outside the continue-sampling region.
. Sampling should stop when the sum of the samples makes an excursion outside the continue-sampling region.
(CCT). The two parameters are p1 and p2 are specified by determining a cutscore (threshold) for examinees on the proportion correct metric, and selecting a point above and below that cutscore. For instance, suppose the cutscore is set at 70% for a test. We could select p1 = 0.65 and p2 = 0.75 . The test then evaluates the likelihood that an examinee's true score on that metric is equal to one of those two points. If the examinee is determined to be at 75%, they pass, and they fail if they are determined to be at 65%.
These points are not specified completely arbitrarily. A cutscore should always be set with a legally defensible method, such as a modified Angoff procedure. Again, the indifference region represents the region of scores that the test designer is OK with going either way (pass or fail). The upper parameter p2 is conceptually the highest level that the test designer is willing to accept for a Fail (because everyone below it has a good chance of failing), and the lower parameter p1 is the lowest level that the test designer is willing to accept for a pass (because everyone above it has a decent chance of passing). While this definition may seem to be a relatively small burden, consider the high-stakes case of a licensing test
for medical doctors: at just what point should we consider somebody to be at one of these two levels?
While the SPRT was first applied to testing in the days of classical test theory
, as is applied in the previous paragraph , Reckase (1983) suggested that item response theory
be used to determine the p1 and p2 parameters. The cutscore and indifference region are defined on the latent ability (theta) metric, and translated onto the proportion metric for computation. Research on CCT since then has applied this methodology for several reasons:
Sequential analysis
In statistics, sequential analysis or sequential hypothesis testing is statistical analysis where the sample size is not fixed in advance. Instead data are evaluated as they are collected, and further sampling is stopped in accordance with a pre-defined stopping rule as soon as significant results...
, developed by Abraham Wald
Abraham Wald
- See also :* Sequential probability ratio test * Wald distribution* Wald–Wolfowitz runs test...
. Neyman and Pearson's 1933 result inspired Wald to reformulate it as a sequential analysis problem. The Neyman-Pearson lemma, by contrast, offers a rule of thumb
Rule of thumb
A rule of thumb is a principle with broad application that is not intended to be strictly accurate or reliable for every situation. It is an easily learned and easily applied procedure for approximately calculating or recalling some value, or for making some determination...
for when all the data is collected (and its likelihood ratio known).
While originally developed for use in quality control
Quality control
Quality control, or QC for short, is a process by which entities review the quality of all factors involved in production. This approach places an emphasis on three aspects:...
studies in the realm of manufacturing, SPRT has been formulated for use in the computerized testing of human examinees as a termination criterion.
Theory
As in classical hypothesis testing, SPRT starts with a pair of hypotheses, say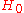 and
and 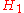 for the null hypothesis
for the null hypothesisNull hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
and alternative hypothesis respectively. They must be specified as follows:
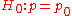
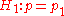
The next step is calculate the cumulative sum of the log-likelihood ratio,
 , as new data arrive:
, as new data arrive:
The stopping rule
Stopping rule
In probability theory, in particular in the study of stochastic processes, a stopping time is a specific type of “random time”....
is a simple thresholding scheme:
-
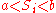 : continue monitoring (critical inequality)
: continue monitoring (critical inequality) -
 : Accept
: Accept 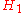
-
 : Accept
: Accept 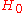
where a and b (
 ) depend on the desired type I and type II errors
) depend on the desired type I and type II errorsType I and type II errors
In statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or...
,
 and
and 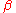 . They may be chosen as follows:
. They may be chosen as follows: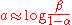 and
and 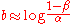
In other words,
 and
and 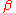 must be decided beforehand in order to set the thresholds appropriately. The numerical value will depend on the application. The reason for using approximation signs is that, in the discrete case, the signal may cross the threshold between samples. Thus, depending on the penalty of making an error and the sampling frequency, one might set the thresholds more aggressively. Of course, the exact bounds may be used in the continuous case.
must be decided beforehand in order to set the thresholds appropriately. The numerical value will depend on the application. The reason for using approximation signs is that, in the discrete case, the signal may cross the threshold between samples. Thus, depending on the penalty of making an error and the sampling frequency, one might set the thresholds more aggressively. Of course, the exact bounds may be used in the continuous case.Example
A textbook example is parameter estimation of a probability distribution functionProbability distribution function
Depending upon which text is consulted, a probability distribution function is any of:* a probability distribution function,* a cumulative distribution function,* a probability mass function, or* a probability density function....
. Let us consider the exponential distribution
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
:

The hypotheses are simply
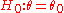 and
and 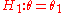 , with
, with  . Then the log-likelihood function (LLF) for one sample is
. Then the log-likelihood function (LLF) for one sample is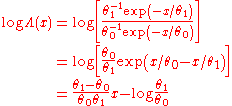
The cumulative sum of the LLFs for all x is
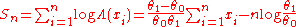
Accordingly, the stopping rule
Stopping rule
In probability theory, in particular in the study of stochastic processes, a stopping time is a specific type of “random time”....
is
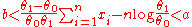
After re-arranging we finally find
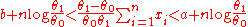
The thresholds are simply two parallel lines
Parallel lines
Parallel Lines may refer to:*Parallel , two straight lines that never touch* Parallel Lines, an album by Blondie*Driver: Parallel Lines, a video game...
with slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
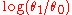 . Sampling should stop when the sum of the samples makes an excursion outside the continue-sampling region.
. Sampling should stop when the sum of the samples makes an excursion outside the continue-sampling region.Manufacturing
The test is done on the proportion metric, and tests that a variable p is equal to one of two desired points, p1 or p2. The region between these two points is known as the indifference region (IR). For example, suppose you are performing a quality control study on a factory lot of widgets. Management would like the lot to have 3% or less defective widgets, but 1% or less is the ideal lot that would pass with flying colors. In this example, p1 = 0.01 and p2 = 0.03 and the region between them is the IR because management considers these lots to be marginal and is OK with them being classified either way. Widgets would be sampled one at a time from the lot (sequential analysis) until the test determines, within an acceptable error level, that the lot is ideal or should be rejected.Testing of human examinees
The SPRT is currently the predominant method of classifying examinees in a variable-length computerized classification testComputerized classification test
A computerized classification test refers to, as its name would suggest, a test that is administered by computer for the purpose of classifying examinees. The most common CCT is a mastery test where the test classifies examinees as "Pass" or "Fail," but the term also includes tests that classify...
(CCT). The two parameters are p1 and p2 are specified by determining a cutscore (threshold) for examinees on the proportion correct metric, and selecting a point above and below that cutscore. For instance, suppose the cutscore is set at 70% for a test. We could select p1 = 0.65 and p2 = 0.75 . The test then evaluates the likelihood that an examinee's true score on that metric is equal to one of those two points. If the examinee is determined to be at 75%, they pass, and they fail if they are determined to be at 65%.
These points are not specified completely arbitrarily. A cutscore should always be set with a legally defensible method, such as a modified Angoff procedure. Again, the indifference region represents the region of scores that the test designer is OK with going either way (pass or fail). The upper parameter p2 is conceptually the highest level that the test designer is willing to accept for a Fail (because everyone below it has a good chance of failing), and the lower parameter p1 is the lowest level that the test designer is willing to accept for a pass (because everyone above it has a decent chance of passing). While this definition may seem to be a relatively small burden, consider the high-stakes case of a licensing test
High-stakes testing
A high-stakes test is a test with important consequences for the test taker. Passing has important benefits, such as a high school diploma, a scholarship, or a license to practice a profession...
for medical doctors: at just what point should we consider somebody to be at one of these two levels?
While the SPRT was first applied to testing in the days of classical test theory
Classical test theory
Classical test theory is a body of related psychometric theory that predict outcomes of psychological testing such as the difficulty of items or the ability of test-takers. Generally speaking, the aim of classical test theory is to understand and improve the reliability of psychological...
, as is applied in the previous paragraph , Reckase (1983) suggested that item response theory
Item response theory
In psychometrics, item response theory also known as latent trait theory, strong true score theory, or modern mental test theory, is a paradigm for the design, analysis, and scoring of tests, questionnaires, and similar instruments measuring abilities, attitudes, or other variables. It is based...
be used to determine the p1 and p2 parameters. The cutscore and indifference region are defined on the latent ability (theta) metric, and translated onto the proportion metric for computation. Research on CCT since then has applied this methodology for several reasons:
- Large item banks tend to be calibrated with IRT
- This allows more accurate specification of the parameters
- By using the item response function for each item, the parameters are easily allowed to vary between items.
See also
- CUSUMCUSUMIn statistical quality control, the CUSUM is a sequential analysis technique due to E. S. Page of the University of Cambridge. It is typically used for monitoring change detection...
- Computerized classification testComputerized classification testA computerized classification test refers to, as its name would suggest, a test that is administered by computer for the purpose of classifying examinees. The most common CCT is a mastery test where the test classifies examinees as "Pass" or "Fail," but the term also includes tests that classify...
- Wald testWald testThe Wald test is a parametric statistical test named after Abraham Wald with a great variety of uses. Whenever a relationship within or between data items can be expressed as a statistical model with parameters to be estimated from a sample, the Wald test can be used to test the true value of the...
- Likelihood-ratio testLikelihood-ratio testIn statistics, a likelihood ratio test is a statistical test used to compare the fit of two models, one of which is a special case of the other . The test is based on the likelihood ratio, which expresses how many times more likely the data are under one model than the other...

