In probability theory

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

, in particular in the study of stochastic process

Stochastic process

In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...

es, a stopping time (also Markov time) is a specific type of “random time”.

The theory of stopping rules and stopping times can be analysed in probability

Probability

Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...

 and statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, notably in the optional stopping theorem

Optional stopping theorem

In probability theory, the optional stopping theorem says that, under certain conditions, the expected value of a martingale at a stopping time is equal to its initial value...

. Also, stopping times are frequently applied in mathematical proofs- to “tame the continuum of time”, as Chung put it in his book (1982).

Definition

A stopping time with respect to a sequence of random variable

Random variable

In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...

s X₁, X₂, ... is a random variable with the property that for each t, the occurrence or non-occurrence of the event  = t depends only on the values of X₁, X₂, ..., X_t. In some cases, the definition specifies that Pr( < ∞) = 1, or that be almost surely

Almost surely

In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...

 finite, although in other cases this requirement is omitted.

Another, more general definition may be given in terms of a filtration: Let 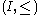be an ordered index set

Index set

In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...

 (often 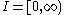or a compact subset thereof), and let 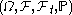be a filtered probability space, i.e. a probability space

Probability space

In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...

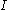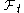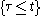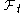 equipped with a filtration. Then a random variable is called a stopping time if for all in . Often, to avoid confusion, we call it a -stopping time and explicitly specify the filtration. Speaking concretely, for to be a stopping time, it should be possible to decide whether or not has occurred on the basis of the knowledge of , i.e., event is -measurable.

Stopping times occur in decision theory

Decision theory

Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...

, in which a stopping rule is characterized as a mechanism for deciding whether to continue or stop a process on the basis of the present position and past events, and which will almost always

Almost Always

"Almost Always" is a popular song. It was recorded by Joni James in 1953. The recording was released by MGM as catalog number 11470. The song was only on the Billboard magazine charts for one week, reaching #18 on May 9, 1953. The flip side was "Is It Any Wonder?"...

 lead to a decision to stop at some time.

Examples

To illustrate some examples of random times that are stopping rules and some that are not, consider a gambler playing roulette

Roulette

Roulette is a casino game named after a French diminutive for little wheel. In the game, players may choose to place bets on either a single number or a range of numbers, the colors red or black, or whether the number is odd or even....

 with a typical house edge, starting with $100:

• Playing one, and only one, game corresponds to the stopping time  = 1, and is a stopping rule.
• Playing until he either runs out of money or has played 500 games is a stopping rule.
• Playing until he is the maximum amount ahead he will ever be is not a stopping rule and does not provide a stopping time, as it requires information about the future as well as the present and past.
• Playing until he doubles his money (borrowing if necessary if he goes into debt) is not a stopping rule, as there is a positive probability
  Probability
  Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
  
   that he will never double his money. (Here it is assumed that there are limits that prevent the employment of a martingale system
  Martingale (betting system)
  Originally, martingale referred to a class of betting strategies popular in 18th century France. The simplest of these strategies was designed for a game in which the gambler wins his stake if a coin comes up heads and loses it if the coin comes up tails...
  
  , or a variant thereof, such as each bet being triple the size of the last. Such limits could include betting limits but not limits to borrowing.)
• Playing until he either doubles his money or runs out of money is a stopping rule, even though there is potentially no limit to the number of games he plays, since the probability that he stops in a finite time is 1.

Localization

Stopping times are frequently used to generalize certain properties of stochastic processes to situations in which the required property is satisfied in only a local sense. First, if X is a process and is a stopping time, then X is used to denote the process X stopped at time .
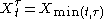
Then, X is said to locally satisfy some property P if there exists a sequence of stopping times _n, which increases to infinity and for which the processes satisfy property P. Common examples, with time index set I = [0,∞), are as follows;

• (Local martingale) A process X is a local martingale
  Local martingale
  In mathematics, a local martingale is a type of stochastic process, satisfying the localized version of the martingale property. Every martingale is a local martingale; every bounded local martingale is a martingale; however, in general a local martingale is not a martingale, because its...
  
   if it is càdlàg
  Càdlàg
  In mathematics, a càdlàg , RCLL , or corlol function is a function defined on the real numbers that is everywhere right-continuous and has left limits everywhere...
  
    and there exists a sequence of stopping times _n increasing to infinity, such that 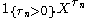is a martingale
  Martingale (probability theory)
  In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
  
   for each n.
• (Locally integrable) A non-negative and increasing process X is locally integrable if there exists a sequence of stopping times _n increasing to infinity, such that for each n.

Types of stopping times

Stopping times, with time index set I = [0,∞), are often divided into one of several types depending on whether it is possible to predict when they are about to occur.

A stopping time is predictable if it is equal to the limit of an increasing sequence of stopping times _n satisfying _n < whenever > 0. The sequence _n is said to announce , and predictable stopping times are sometimes known as announceable.
Examples of predictable stopping times are hitting time

Hitting time

In the study of stochastic processes in mathematics, a hitting time is a particular instance of a stopping time, the first time at which a given process "hits" a given subset of the state space...

s of continuous and adapted

Adapted process

In the study of stochastic processes, an adapted process is one that cannot "see into the future". An informal interpretation is that X is adapted if and only if, for every realisation and every n, Xn is known at time n...

 processes. If is the first time at which a continuous and real valued process X is equal to some value a, then it is announced by the sequence _n, where _n is the first time at which X is within a distance of 1/n of a.

Accessible stopping times are those that can be covered by a sequence of predictable times. That is, stopping time is accessible if, P(=_n for some n) = 1, where _n are predictable times.

A stopping time is totally inaccessible if it can never be announced by an increasing sequence of stopping times. Equivalently, P( = σ < ∞) = 0 for every predictable time σ. Examples of totally inaccessible stopping times include the jump times of Poisson process

Poisson process

A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...

es.

Every stopping time can be uniquely decomposed into an accessible and totally inaccessible time. That is, there exists a unique accessible stopping time σ and totally inaccessible time υ such that = σ whenever σ < ∞, = υ whenever υ < ∞, and = ∞ whenever σ = υ = ∞.
Note that in the statement of this decomposition result, stopping times do not have to be almost surely finite, and can equal ∞.

See also

• Optimal stopping
  Optimal stopping
  In mathematics, the theory of optimal stopping is concerned with the problem of choosing a time to take a particular action, in order to maximise an expected reward or minimise an expected cost. Optimal stopping problems can be found in areas of statistics, economics, and mathematical finance...
  
  
• Odds algorithm
  Odds algorithm
  The odds-algorithm is a mathematical method for computing optimalstrategies for a class of problems that belong to the domain of optimal stopping problems. Their solution follows from the odds-strategy, and the importance of the...
  
  
• Secretary problem
  Secretary problem
  The secretary problem is one of many names for a famous problem of theoptimal stopping theory.The problem has been studied extensively in the fields ofapplied probability, statistics, and decision theory...
  
  
• Hitting time
  Hitting time
  In the study of stochastic processes in mathematics, a hitting time is a particular instance of a stopping time, the first time at which a given process "hits" a given subset of the state space...
  
  
• Stopped process
  Stopped process
  In mathematics, a stopped process is a stochastic process that is forced to assume the same value after a prescribed time.-Definition:Let* be a probability space;...
  
  
• Disorder problem
  Disorder problem
  In the study of stochastic processes in mathematics, a disorder problem has been formulated by Kolmogorov. Specifically, the problem is use ongoing observations on a stochastic process to decide whether or not to raise an alarm that the probabilistic properties of the process have changed.An...
  
  
• Parking problem
• Quick detection

Further reading

• Thomas S. Ferguson. “Who solved the secretary problem?”, Stat. Sci. vol. 4, 282–296, (1989).
• An introduction to stopping times.
• F. Thomas Bruss, “Sum the odds to one and stop”, Annals of Probability, Vol. 4, 1384–1391,(2000)