
Rolle's theorem
Encyclopedia
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
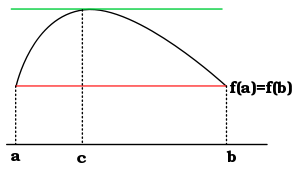
, Rolle's theorem essentially states that a differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
which attains equal values at two distinct points must have a point
Stationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
somewhere between them where the first derivative (the slope of the tangent line to the graph of the function) is zero.
Standard version of the theorem
If a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued function ƒ is continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on a closed interval [a, b], differentiable
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
on the open interval (a, b), and ƒ(a) = ƒ(b), then there exists a c in the open interval (a, b) such that

This version of Rolle's theorem is used to prove the mean value theorem
Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
, of which Rolle's theorem is indeed a special case. It is also the basis for the proof of the Taylor's theorem
Taylor's theorem
In calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
.
History
The first known formal proof was offered by Michel RolleMichel Rolle
Michel Rolle was a French mathematician. He is best known for Rolle's theorem , and he deserves to be known as the co-inventor in Europe of Gaussian elimination .-Life:...
in 1691, which used the methods of differential calculus.
The name "Rolle's theorem" was first used by Moritz Wilhelm Drobisch
Moritz Wilhelm Drobisch
Moritz Wilhelm Drobisch was a German mathematician, logician, psychologist and philosopher. His brother was the composer Karl Ludwig Drobisch .-Life:...
of Germany in 1834 and by Giusto Bellavitis
Giusto Bellavitis
Giusto Bellavitis was an Italian mathematician. He is known for his contributions to algebraic geometry.-Awards:* Fellow of the Istituto Veneto in 1840* Fellow of the Società Italiana dei Quaranta in 1850...
of Italy in 1846.
First example
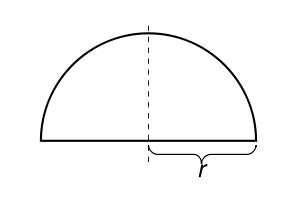
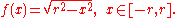
Its graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
is the upper semicircle
Semicircle
In mathematics , a semicircle is a two-dimensional geometric shape that forms half of a circle. Being half of a circle's 360°, the arc of a semicircle always measures 180° or a half turn...
centered at the origin. This function is continuous on the closed interval [−r,r] and differentiable in the open interval (−r,r), but not differentiable at the endpoints −r and r. Since f(−r) = f(r), Rolle's theorem applies, and indeed, there is a point where the derivative of f is zero. Note that the theorem applies even when the function cannot be differentiated at the endpoints because it only requires the function to be differentiable in the open interval.
Second example

Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
function

Then f(−1) = f(1), but there is no c between −1 and 1 for which the derivative is zero. This is because that function, although continuous, is not differentiable at x = 0. Note that the derivative of f changes its sign at x = 0, but without attaining the value 0. The theorem cannot be applied to this function, clearly, because it does not satisfy the condition that the function must be differentiable for every x in the open interval.
Generalization
The second example illustrates the following generalization of Rolle's theorem:Consider a real-valued, continuous function f on a closed interval [a,b] with f(a) = f(b). If for every x in the open interval (a,b) the right-hand limit

and the left-hand limit

exist in the extended real line [−∞,∞], then there is some number c in the open interval (a,b) such that one of the two limits

is ≥ 0 and the other one is ≤ 0 (in the extended real line). If the right- and left-hand limit agree for every x, then they agree in particular for c, hence the derivative of f exists at c and is equal to zero.
Remarks
- If f is convex or concave, then the right- and left-hand derivatives exist at every inner point, hence the above limits exist and are real numbers.
- This generalized version of the theorem is sufficient to prove convexityConvex functionIn mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
when the one-sided derivatives are monotonically increasing:
Proof of the generalized version
Since the proof for the standard version of Rolle's theorem and the generalization are very similar, we prove the generalization.The idea of the proof is to argue that if f(a) = f(b), then f must attain either a maximum
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
or a minimum somewhere between a and b, say at c, and the function must change from increasing to decreasing (or the other way around) at c. In particular, if the derivative exists, it must be zero at c.
By assumption, f is continuous on [a,b], and by the extreme value theorem
Extreme value theorem
In calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
attains both its maximum and its minimum in [a,b]. If these are both attained at the endpoints of [a,b], then f is constant
Constant function
In mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
on [a,b] and so the derivative of f is zero at every point in (a,b).
Suppose then that the maximum is obtained at an interior point c of (a,b) (the argument for the minimum is very similar, just consider −f ). We shall examine the above right- and left-hand limits separately.
For a real h such that c + h is in [a,b], the value f(c + h) is smaller or equal to f(c) because f attains its maximum at c. Therefore, for every h > 0,
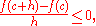
hence
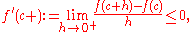
where the limit exists by assumption, it may be minus infinity.
Similarly, for every h < 0, the inequality turns around because the denominator is now negative and we get

hence
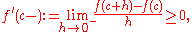
where the limit might be plus infinity.
Finally, when the above right- and left-hand limits agree (in particular when f is differentiable), then the derivative of f at c must be zero.
Generalization to higher derivatives
We can also generalize Rolle's theorem by requiring that f has more points with equal values and greater regularity. Specifically, suppose that- the function f is n − 1 times continuously differentiable on the closed interval [a,b] and the nth derivative exists on the open interval (a,b), and
- there are n intervals given by a1 < b1 ≤ a2 < b2 ≤ . . .≤ an < bn in [a,b] such that f(ak) = f(bk) for every k from 1 to n.
Then there is a number c in (a,b) such that the nth derivative of f at c is zero.
Of course, the requirements concerning the nth derivative of f can be weakened as in the generalization above, giving the corresponding (possibly weaker) assertions for the right- and left-hand limits defined above with f (n−1) in place of f.
Proof
The proof uses mathematical inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. For n = 1 is simply the standard version of Rolle's theorem. As induction hypothesis, assume the generalization is true for n − 1. We want to prove it for n > 1. By the standard version of Rolle's theorem, for every integer k from 1 to n, there exists a ck in the open interval (ak,bk) such that f
Generalizations to other fields
Rolle's theorem is a property of differentiable functions over the real numbers, which are an ordered fieldOrdered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
. As such, it does not generalize to other fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, but the following corollary does: if a real polynomial splits (has all its roots) over the real numbers, then its derivative does as well – one may call this property of a field Rolle's property. More general fields do not always have a notion of differentiable function, but they do have a notion of polynomials, which can be symbolically differentiated. Similarly, more general fields may not have an order, but one has a notion of a root of a polynomial lying in a field.
Thus Rolle's theorem shows that the real numbers have Rolle's property, and any algebraically closed field such as the complex numbers has Rolle's property, but conversely the rational numbers do not – for example,
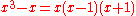 splits over the rationals, but its derivative
splits over the rationals, but its derivative 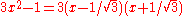 does not. The question of which fields satisfy Rolle's property was raised in . For finite field
does not. The question of which fields satisfy Rolle's property was raised in . For finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s, the answer is that only
 and
and 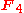 have Rolle's property; this was first proven via technical means in , and a simple proof is given in .
have Rolle's property; this was first proven via technical means in , and a simple proof is given in .For a complex version, see Voorhoeve index
Voorhoeve index
Rolle's theorem states that if f is a continuously differentiable real-valued function on the real line, and f = f = 0, where a < b, then its derivative f ' must have a zero strictly between a and b...
.
External links
- Rolle's and Mean Value Theorems at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...


