
Productive set
Encyclopedia
In computability theory
, productive sets and creative sets are types of sets of natural number
s that have important applications in mathematical logic
. They are a standard topic in mathematical logic textbooks such as Soare (1987) and Rogers (1987).
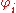 is an acceptable numbering of the computable function
is an acceptable numbering of the computable function
s and Wi the corresponding numbering of the recursively enumerable sets.
A set A of natural numbers is called productive if there exists a partial
computable function so that for all
so that for all 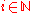 , if
, if  then
then  The function
The function  is called the productive function for
is called the productive function for 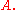
A set A of natural numbers is called creative if A is recursively enumerable and its complement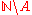 is productive. Not every productive set has a recursively enumerable complement, however, as illustrated below.
is productive. Not every productive set has a recursively enumerable complement, however, as illustrated below.
The archetypal creative set is , the set representing the halting problem
, the set representing the halting problem
. Its complement is productive with productive function f(i) = i. To see this, assume
is productive with productive function f(i) = i. To see this, assume 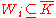 . If i were in
. If i were in  then
then 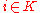 and thus
and thus 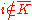 . This would mean
. This would mean 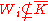 , so we can conclude
, so we can conclude 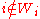 , which means
, which means 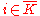 .
.
Any productive set has a productive function that is injective
and total.
The following theorems, due to Myhill (1955), show that in a sense all creative sets are like and all productive sets are like
and all productive sets are like  (see Soare (1987) and Rogers (1987)).
(see Soare (1987) and Rogers (1987)).
Theorem. Let P be a set of natural numbers. The following are equivalent:
Theorem. Let C be a set of natural numbers. The following are equivalent:
is always a recursively enumerable set
. If the system is suitably complex, like first-order arithmetic, then the set T of Gödel number
s of true sentences in the system will be a productive set, which means that whenever W is a recursively enumerable set of true sentences, there is at least one true sentence that is not in W. This can be used to give a rigorous proof of Gödel's first incompleteness theorem, because no recursively enumerable set is productive. The complement of the set T will not be recursively enumerable, and thus T is an example of a productive set whose complement is not creative.
Recursion theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, productive sets and creative sets are types of sets of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s that have important applications in mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
. They are a standard topic in mathematical logic textbooks such as Soare (1987) and Rogers (1987).
Definition and example
For the remainder of this article, assume that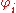 is an acceptable numbering of the computable function
is an acceptable numbering of the computable functionComputable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
s and Wi the corresponding numbering of the recursively enumerable sets.
A set A of natural numbers is called productive if there exists a partial
Partial function
In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...
computable function
 so that for all
so that for all 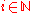 , if
, if  then
then  The function
The function  is called the productive function for
is called the productive function for 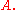
A set A of natural numbers is called creative if A is recursively enumerable and its complement
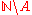 is productive. Not every productive set has a recursively enumerable complement, however, as illustrated below.
is productive. Not every productive set has a recursively enumerable complement, however, as illustrated below. The archetypal creative set is
 , the set representing the halting problem
, the set representing the halting problemHalting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
. Its complement
 is productive with productive function f(i) = i. To see this, assume
is productive with productive function f(i) = i. To see this, assume 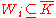 . If i were in
. If i were in  then
then 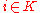 and thus
and thus 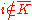 . This would mean
. This would mean 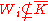 , so we can conclude
, so we can conclude 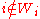 , which means
, which means 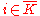 .
.Properties
No productive set A can be recursively enumerable, because whenever A contains every number in an r.e. set Wi it contains other numbers, and moreover there is an effective procedure to produce an example of such a number from the index i. Similarly, no creative set can be decidable, because this would imply that its complement, a productive set, is recursively enumerable.Any productive set has a productive function that is injective
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
and total.
The following theorems, due to Myhill (1955), show that in a sense all creative sets are like
 and all productive sets are like
and all productive sets are like  (see Soare (1987) and Rogers (1987)).
(see Soare (1987) and Rogers (1987)).Theorem. Let P be a set of natural numbers. The following are equivalent:
- P is productive.
 is 1-reducibleMany-one reductionIn computability theory and computational complexity theory, a many-one reduction is a reduction which converts instances of one decision problem into instances of a second decision problem. Reductions are thus used to measure the relative computational difficulty of two problems.Many-one...
is 1-reducibleMany-one reductionIn computability theory and computational complexity theory, a many-one reduction is a reduction which converts instances of one decision problem into instances of a second decision problem. Reductions are thus used to measure the relative computational difficulty of two problems.Many-one...
to P. is m-reducibleMany-one reductionIn computability theory and computational complexity theory, a many-one reduction is a reduction which converts instances of one decision problem into instances of a second decision problem. Reductions are thus used to measure the relative computational difficulty of two problems.Many-one...
is m-reducibleMany-one reductionIn computability theory and computational complexity theory, a many-one reduction is a reduction which converts instances of one decision problem into instances of a second decision problem. Reductions are thus used to measure the relative computational difficulty of two problems.Many-one...
to P.
Theorem. Let C be a set of natural numbers. The following are equivalent:
- C is creative.
- C is 1-completeMany-one reductionIn computability theory and computational complexity theory, a many-one reduction is a reduction which converts instances of one decision problem into instances of a second decision problem. Reductions are thus used to measure the relative computational difficulty of two problems.Many-one...
- C is recursively isomorphic to K, that is, there is a total computable bijection f on the natural numbers such that f(C) = K.
Applications in mathematical logic
The set of all provable sentences in an effective axiomatic systemAxiomatic system
In mathematics, an axiomatic system is any set of axioms from which some or all axioms can be used in conjunction to logically derive theorems. A mathematical theory consists of an axiomatic system and all its derived theorems...
is always a recursively enumerable set
Recursively enumerable set
In computability theory, traditionally called recursion theory, a set S of natural numbers is called recursively enumerable, computably enumerable, semidecidable, provable or Turing-recognizable if:...
. If the system is suitably complex, like first-order arithmetic, then the set T of Gödel number
Gödel number
In mathematical logic, a Gödel numbering is a function that assigns to each symbol and well-formed formula of some formal language a unique natural number, called its Gödel number. The concept was famously used by Kurt Gödel for the proof of his incompleteness theorems...
s of true sentences in the system will be a productive set, which means that whenever W is a recursively enumerable set of true sentences, there is at least one true sentence that is not in W. This can be used to give a rigorous proof of Gödel's first incompleteness theorem, because no recursively enumerable set is productive. The complement of the set T will not be recursively enumerable, and thus T is an example of a productive set whose complement is not creative.

