
Raychaudhuri equation
Encyclopedia
In general relativity
, the Raychaudhuri equation, or Landau-Raychaudhuri equation, is a fundamental result describing the motion of nearby bits of matter.
The equation is important as a fundamental lemma for the Penrose-Hawking singularity theorems
and for the study of exact solutions in general relativity
, but has independent interest, since it offers a simple and general validation of our intuitive expectation that gravitation
should be a universal attractive force between any two bits of mass-energy in general relativity, as it is in Newton's theory of gravitation.
The equation was discovered independently by Amal Kumar Raychaudhuri
and Lev Landau
.
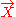 (which can be interpreted as a family or congruence
(which can be interpreted as a family or congruence
of nonintersecting world line
s, not necessarily geodesic
s), Raychaudhuri's equation can be written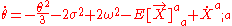
where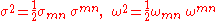
are (non-negative) quadratic invariants of the shear tensor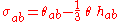
and the vorticity tensor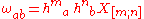
respectively. Here,
is the expansion tensor,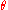 is its trace
is its trace
, called the expansion scalar, and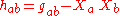
is the projection tensor onto the hyperplanes orthogonal to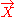 . Also, dot denotes differentiation with respect to proper time
. Also, dot denotes differentiation with respect to proper time
counted along the world lines in the congruence. Finally, the trace of the tidal tensor
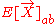 can also be written
can also be written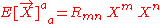
This quantity is sometimes called the Raychaudhuri scalar.
The shear tensor measures any tendency of an initially spherical ball of matter to become distorted into an ellipsoidal shape. The vorticity tensor measures any tendency of nearby world lines to twist about one another (if this happens, our small blob of matter is rotating, as happens to fluid elements in an ordinary fluid flow which exhibits nonzero vorticity).
The right hand side of Raychaudhuri's equation consists of two types of terms:
Usually one term will win out. However there are situations in which a balance can be achieved. This balance may be:
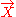 be a timelike geodesic unit vector field with vanishing vorticity, or equivalently, which is hypersurface orthogonal. For example, this situation can arise in studying the world lines of the dust particles in cosmological models which are exact dust solutions of the Einstein field equation (provided that these world lines are not twisting about one another, in which case the congruence would have nonzero vorticity).
be a timelike geodesic unit vector field with vanishing vorticity, or equivalently, which is hypersurface orthogonal. For example, this situation can arise in studying the world lines of the dust particles in cosmological models which are exact dust solutions of the Einstein field equation (provided that these world lines are not twisting about one another, in which case the congruence would have nonzero vorticity).
Then Raychaudhuri's equation becomes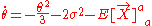
Now the right hand side is always negative, so even if the expansion scalar is initially positive (if our small ball of dust is initially increasing in volume), eventually it must become negative (our ball of dust must recollapse).
Indeed, in this situation we have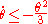
Integrating this inequality with respect to proper time gives
gives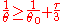
If the initial value of the expansion scalar is negative, this means that our geodesics must converge in a caustic
of the expansion scalar is negative, this means that our geodesics must converge in a caustic
(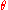 goes to minus infinity) within a proper time of at most
goes to minus infinity) within a proper time of at most 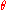 after the measurement of the initial value
after the measurement of the initial value  of the expansion scalar. This need not signal an encounter with a curvature singularity, but it does signal a breakdown in our mathematical description of the motion of the dust.
of the expansion scalar. This need not signal an encounter with a curvature singularity, but it does signal a breakdown in our mathematical description of the motion of the dust.
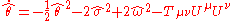 .
.
Here, the hats indicate the expansion, shear and vorticity are only with respect to the transverse directions.
When the vorticity is zero, then assuming the null energy condition, caustics will form before the affine parameter reaches .
.
is defined as the boundary of the causal past of null infinity. Such boundaries are generated by null geodesics. The affine parameter goes to infinity as we approach null infinity, and no caustics form until then. So, the expansion of the event horizon has to be nonnegative. As the expansion gives the rate of change of the logarithm of the area density, this means the event horizon area can never go down, at least classically, assuming the null energy condition.
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the Raychaudhuri equation, or Landau-Raychaudhuri equation, is a fundamental result describing the motion of nearby bits of matter.
The equation is important as a fundamental lemma for the Penrose-Hawking singularity theorems
Penrose-Hawking singularity theorems
The Penrose–Hawking singularity theorems are a set of results in general relativity which attempt to answer the question of when gravitation produces singularities.A singularity in solutions of the Einstein field equations is one of two things:...
and for the study of exact solutions in general relativity
Exact solutions in general relativity
In general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
, but has independent interest, since it offers a simple and general validation of our intuitive expectation that gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
should be a universal attractive force between any two bits of mass-energy in general relativity, as it is in Newton's theory of gravitation.
The equation was discovered independently by Amal Kumar Raychaudhuri
Amal Kumar Raychaudhuri
Amal Kumar Raychaudhuri was a leading physicist well known for his contributions to relativistic cosmology, particularly Raychaudhuri's equation, which is a key ingredient in proving the Penrose-Hawking singularity theorems of general relativity...
and Lev Landau
Lev Landau
Lev Davidovich Landau was a prominent Soviet physicist who made fundamental contributions to many areas of theoretical physics...
.
Mathematical statement
Given a timelike unit vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
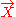 (which can be interpreted as a family or congruence
(which can be interpreted as a family or congruenceCongruence (general relativity)
In general relativity, a congruence is the set of integral curves of a vector field in a four-dimensional Lorentzian manifold which is interpreted physically as a model of spacetime...
of nonintersecting world line
World line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
s, not necessarily geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s), Raychaudhuri's equation can be written
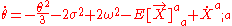
where
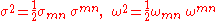
are (non-negative) quadratic invariants of the shear tensor
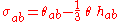
and the vorticity tensor
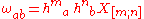
respectively. Here,

is the expansion tensor,
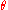 is its trace
is its traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
, called the expansion scalar, and
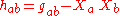
is the projection tensor onto the hyperplanes orthogonal to
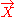 . Also, dot denotes differentiation with respect to proper time
. Also, dot denotes differentiation with respect to proper timeProper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
counted along the world lines in the congruence. Finally, the trace of the tidal tensor
Electrogravitic tensor
In general relativity, the tidal tensor or gravitoelectric tensor is one of the pieces in the Bel decomposition of the Riemann tensor. It is physically interpreted as giving the tidal stresses on small bits of a material object , or the tidal accelerations of a small cloud of test particles in a...
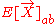 can also be written
can also be written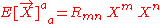
This quantity is sometimes called the Raychaudhuri scalar.
Intuitive significance
The expansion scalar measures the fractional rate at which the volume of a small ball of matter changes with respect to time as measured by a central comoving observer (and so it may take negative values). In other words, the above equation gives us the evolution equation for the expansion of the timelike congruence. If the derivative (with respect to proper time) of this quantity turns out to be negative along some world line (after a certain event), then any expansion of a small ball of matter (whose center of mass follows the world line in question) must be followed by recollapse. If not, continued expansion is possible.The shear tensor measures any tendency of an initially spherical ball of matter to become distorted into an ellipsoidal shape. The vorticity tensor measures any tendency of nearby world lines to twist about one another (if this happens, our small blob of matter is rotating, as happens to fluid elements in an ordinary fluid flow which exhibits nonzero vorticity).
The right hand side of Raychaudhuri's equation consists of two types of terms:
- terms which promote (re)-collapse
- initially nonzero expansion scalar,
- nonzero shearing,
- positive trace of the tidal tensor; this is precisely the condition guaranteed by assuming the strong energy condition, which holds for the most important types of solutions, such as physically reasonable fluid solutionFluid solutionIn general relativity, a fluid solution is an exact solution of the Einstein field equation in which the gravitational field is produced entirely by the mass, momentum, and stress density of a fluid....
s),
- terms which oppose (re)-collapse
- nonzero vorticity, corresponding to Newtonian centrifugal forceCentrifugal forceCentrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
s, - positive divergence of the acceleration vector (e.g., outward pointing acceleration due to a spherically symmetric explosion, or more prosaically, due to body forces on fluid elements in a ball of fluid held together by its own self-gravitation).
- nonzero vorticity, corresponding to Newtonian centrifugal force
Usually one term will win out. However there are situations in which a balance can be achieved. This balance may be:
- stable: in the case of hydrostatic equilibriumHydrostatic equilibriumHydrostatic equilibrium or hydrostatic balance is the condition in fluid mechanics where a volume of a fluid is at rest or at constant velocity. This occurs when compression due to gravity is balanced by a pressure gradient force...
of a ball of perfect fluid (e.g. in a model of a stellar interior), the expansion, shear, and vorticity all vanish, and a radial divergence in the acceleration vector (the necessary body forceBody forceA body force is a force that acts throughout the volume of a body, in contrast to contact forces.Gravity and electromagnetic forces are examples of body forces. Centrifugal and Coriolis forces can also be viewed as body forces.This can be put into contrast to the classical definition of surface...
on each blob of fluid being provided by the pressure of surrounding fluid) counteracts the Raychaudhuri scalar, which for a perfect fluid is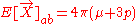 . In Newtonian gravitation, the trace of the tidal tensor is
. In Newtonian gravitation, the trace of the tidal tensor is  ; in general relativity, the tendency of pressure to oppose gravity is partially offset by this term, which under certain circumstances can become important.
; in general relativity, the tendency of pressure to oppose gravity is partially offset by this term, which under certain circumstances can become important. - unstable: for example, the world lines of the dust particles in the Gödel solutionGödel metricThe Gödel metric is an exact solution of the Einstein field equations in which the stress-energy tensor contains two terms, the first representing the matter density of a homogeneous distribution of swirling dust particles, and the second associated with a nonzero cosmological constant...
have vanishing shear, expansion, and acceleration, but constant vorticity just balancing a constant Raychuadhuri scalar due to nonzero vacuum energy ("cosmological constant").
Focusing theorem
Suppose the strong energy condition holds in some region of our spacetime, and let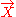 be a timelike geodesic unit vector field with vanishing vorticity, or equivalently, which is hypersurface orthogonal. For example, this situation can arise in studying the world lines of the dust particles in cosmological models which are exact dust solutions of the Einstein field equation (provided that these world lines are not twisting about one another, in which case the congruence would have nonzero vorticity).
be a timelike geodesic unit vector field with vanishing vorticity, or equivalently, which is hypersurface orthogonal. For example, this situation can arise in studying the world lines of the dust particles in cosmological models which are exact dust solutions of the Einstein field equation (provided that these world lines are not twisting about one another, in which case the congruence would have nonzero vorticity).Then Raychaudhuri's equation becomes
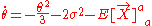
Now the right hand side is always negative, so even if the expansion scalar is initially positive (if our small ball of dust is initially increasing in volume), eventually it must become negative (our ball of dust must recollapse).
Indeed, in this situation we have
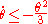
Integrating this inequality with respect to proper time
 gives
gives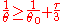
If the initial value
 of the expansion scalar is negative, this means that our geodesics must converge in a caustic
of the expansion scalar is negative, this means that our geodesics must converge in a causticCaustic (mathematics)
In differential geometry and geometric optics, a caustic is the envelope of rays either reflected or refracted by a manifold. It is related to the optical concept of caustics...
(
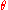 goes to minus infinity) within a proper time of at most
goes to minus infinity) within a proper time of at most 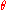 after the measurement of the initial value
after the measurement of the initial value  of the expansion scalar. This need not signal an encounter with a curvature singularity, but it does signal a breakdown in our mathematical description of the motion of the dust.
of the expansion scalar. This need not signal an encounter with a curvature singularity, but it does signal a breakdown in our mathematical description of the motion of the dust.Optical equations
There is also an optical (or null) version of Raychaudhuri's equation for null geodesic congruences.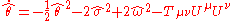 .
.Here, the hats indicate the expansion, shear and vorticity are only with respect to the transverse directions.
When the vorticity is zero, then assuming the null energy condition, caustics will form before the affine parameter reaches
 .
.Applications
The event horizonEvent horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
is defined as the boundary of the causal past of null infinity. Such boundaries are generated by null geodesics. The affine parameter goes to infinity as we approach null infinity, and no caustics form until then. So, the expansion of the event horizon has to be nonnegative. As the expansion gives the rate of change of the logarithm of the area density, this means the event horizon area can never go down, at least classically, assuming the null energy condition.
See also
- congruence (general relativity)Congruence (general relativity)In general relativity, a congruence is the set of integral curves of a vector field in a four-dimensional Lorentzian manifold which is interpreted physically as a model of spacetime...
, for a derivation of the kinematical decomposition and of Raychaudhuri's equation. - Gravitational singularityGravitational singularityA gravitational singularity or spacetime singularity is a location where the quantities that are used to measure the gravitational field become infinite in a way that does not depend on the coordinate system...
- Penrose-Hawking singularity theoremsPenrose-Hawking singularity theoremsThe Penrose–Hawking singularity theorems are a set of results in general relativity which attempt to answer the question of when gravitation produces singularities.A singularity in solutions of the Einstein field equations is one of two things:...
for an application of the focusing theorem.
External links
- The Meaning of Einstein's Field Equation by John C. Baez and Emory F. Bunn. Raychaudhuri's equation takes center stage in this well known (and highly recommended) semi-technical exposition of what Einstein's equation says.

