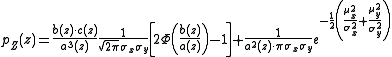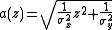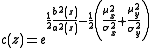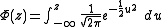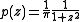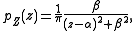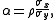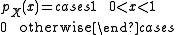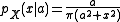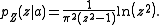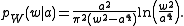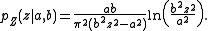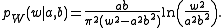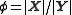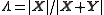Ratio distribution
Encyclopedia
A ratio distribution is a probability distribution
constructed as the distribution of the ratio
of random variable
s having two other known distributions.
Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio
is a ratio distribution.
The Cauchy distribution
is an example of a ratio distribution. The random variable associated with this distribution comes about as the ratio of two Gaussian (normal) distributed variables with zero mean.
Thus the Cauchy distribution is also called the normal ratio distribution.
A number of researchers have considered more general ratio distributions.
Two distributions often used in test-statistics, the t-distribution and the F-distribution, are also ratio distributions:
The t-distributed random variable is the ratio of a Gaussian random variable divided by an independent chi-distributed random variable (i.e., the square root of a chi-squared distribution),
while the F-distributed random variable is the ratio of two independent chi-squared distributed random variables.
Often the ratio distributions are heavy-tailed, and it may be difficult to work with such distributions and develop an associated statistical test.
A method based on the median
has been suggested as a "work-around".
Related to the ratio distribution are the product distribution
, sum distribution and difference distribution. More generally, one may talk of combinations of sums, differences, products and ratios.
Many of these distributions are described in Melvin D. Springer's book from 1979 The Algebra of Random Variables.
The algebraic rules known with ordinary numbers do not apply for the algebra of random variables.
For example, if a product is C = AB and a ratio is D=C/A it does not necessarily mean that the distributions of D and B are the same.
Indeed, a peculiar effect is seen for the Cauchy distribution
: The product and the ratio of two independent Cauchy distributions (with the same scale parameter and the location parameter set to zero) will give the same distribution.
This becomes evident when regarding the Cauchy distribution as itself a ratio distribution of two Gaussian distributions: Consider two Cauchy random variables,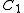
and 
each constructed from two Gaussian distributions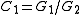 
and 
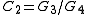then
where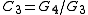
. The first term is the ratio of two Cauchy distributions while the last term is the product of two such distributions.
This is not always straightforward.
The Mellin transform
has also been suggested for derivation of ratio distributions.
It is a Cauchy distribution
.
However, when the two distributions have non-zero mean then the form for the distribution of the ratio is much more complicated.
In 1969 David Hinkley found a form for this distribution. In the absence of correlation (cor(X,Y) = 0), the probability density function
of the two normal variable X = N(μX, σX2) and Y = N(μY, σY2) ratio Z = X/Y is given by the following expression:
where
The above expression becomes even more complicated if the variables X and Y are correlated.
It can also be shown that p(z) is a standard Cauchy distribution
if μX = μY = 0, and σX = σY = 1. In such case b(z) = 0, and
If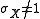
, 
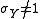or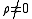 
the more general Cauchy distribution is obtained
where ρ is the correlation coefficient
between X and Y and
The complex distribution has also been expressed with Kummer's confluent hypergeometric function
or the Hermite function.
The transformation has been called the Geary–Hinkley transformation, and the approximation is good if Y is unlikely to assume negative values.
, e.g.,
the ratio distribution becomes
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
constructed as the distribution of the ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
of random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s having two other known distributions.
Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio
is a ratio distribution.
The Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
is an example of a ratio distribution. The random variable associated with this distribution comes about as the ratio of two Gaussian (normal) distributed variables with zero mean.
Thus the Cauchy distribution is also called the normal ratio distribution.
A number of researchers have considered more general ratio distributions.
Two distributions often used in test-statistics, the t-distribution and the F-distribution, are also ratio distributions:
The t-distributed random variable is the ratio of a Gaussian random variable divided by an independent chi-distributed random variable (i.e., the square root of a chi-squared distribution),
while the F-distributed random variable is the ratio of two independent chi-squared distributed random variables.
Often the ratio distributions are heavy-tailed, and it may be difficult to work with such distributions and develop an associated statistical test.
A method based on the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
has been suggested as a "work-around".
Algebra of random variables
The ratio is one type of algebra for random variables:Related to the ratio distribution are the product distribution
Product distribution
A product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions...
, sum distribution and difference distribution. More generally, one may talk of combinations of sums, differences, products and ratios.
Many of these distributions are described in Melvin D. Springer's book from 1979 The Algebra of Random Variables.
The algebraic rules known with ordinary numbers do not apply for the algebra of random variables.
For example, if a product is C = AB and a ratio is D=C/A it does not necessarily mean that the distributions of D and B are the same.
Indeed, a peculiar effect is seen for the Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
: The product and the ratio of two independent Cauchy distributions (with the same scale parameter and the location parameter set to zero) will give the same distribution.
This becomes evident when regarding the Cauchy distribution as itself a ratio distribution of two Gaussian distributions: Consider two Cauchy random variables,
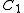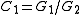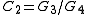and each constructed from two Gaussian distributions and then
where
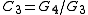. The first term is the ratio of two Cauchy distributions while the last term is the product of two such distributions.Derivation
A way of deriving the ratio distribution of Z from the joint distribution of the two other random variables, X and Y, is by integration of the following form
This is not always straightforward.
The Mellin transform
Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
has also been suggested for derivation of ratio distributions.
Gaussian ratio distribution
When X and Y are independent and have a Gaussian distribution with zero mean the form of their ratio distribution is fairly simple:It is a Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
.
However, when the two distributions have non-zero mean then the form for the distribution of the ratio is much more complicated.
In 1969 David Hinkley found a form for this distribution. In the absence of correlation (cor(X,Y) = 0), the probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of the two normal variable X = N(μX, σX2) and Y = N(μY, σY2) ratio Z = X/Y is given by the following expression:
where
The above expression becomes even more complicated if the variables X and Y are correlated.
It can also be shown that p(z) is a standard Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
if μX = μY = 0, and σX = σY = 1. In such case b(z) = 0, and
If
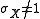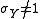, or 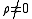the more general Cauchy distribution is obtained
where ρ is the correlation coefficient
Pearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
between X and Y and
The complex distribution has also been expressed with Kummer's confluent hypergeometric function
Confluent hypergeometric function
In mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity...
or the Hermite function.
A transformation to Gaussianity
A transformation has been suggested so that, under certain assumptions, the transformed variable T would approximately have a standard Gaussian distribution:
The transformation has been called the Geary–Hinkley transformation, and the approximation is good if Y is unlikely to assume negative values.
Uniform ratio distribution
With two independent random variables following a uniform distributionUniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
, e.g.,
the ratio distribution becomes
-
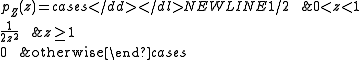
Cauchy ratio distribution
If two independent random variables, X and Y each follow a Cauchy distributionCauchy distributionThe Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
with median equal to zero and shape factor
then the ratio distribution for the random variable
is
Interestingly, this distribution does not depend on
and it should be noted that the result stated by Springer (p158 Question 4.6) is not correct.
The ratio distribution is similar to but not the same as the product distributionProduct distributionA product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions...
of the random variable
:
More generally, if two independent random variables X and Y each follow a Cauchy distributionCauchy distributionThe Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
with median equal to zero and shape factor
and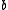 
respectively, then:
1. The ratio distribution for the random variable
is
2. The product distributionProduct distributionA product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions...
for the random variable
is
The result for the ratio distribution can be obtained from the product distribution by replacing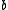
with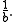 
Ratio of standard normal to standard uniform
If X has a standard normal distribution and Y has a standard uniform distribution, then Z = X / Y has a distribution known as the slash distributionSlash distributionIn probability theory, the slash distribution is the probability distribution of a standard normal variate divided by an independent standard uniform variate...
, with probability density function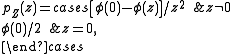
where φ(z) is the probability density function of the standard normal distribution.
Ratio distributions in multivariate analysis
Ratio distributions also appear in multivariate analysisMultivariate analysisMultivariate analysis is based on the statistical principle of multivariate statistics, which involves observation and analysis of more than one statistical variable at a time...
.
If the random matrices X and Y follow a Wishart distribution then the ratio of the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
s
is proportional to the product of independent F random variables. In the case where X and Y are from independent standardized Wishart distributions then the ratio
has a Wilks' lambda distributionWilks' lambda distributionIn statistics, Wilks' lambda distribution , is a probability distribution used in multivariate hypothesis testing, especially with regard to the likelihood-ratio test and Multivariate analysis of variance...
.
See also
- Algebra of random variablesAlgebra of random variablesIn the algebraic axiomatization of probability theory, the primary concept is not that of probability of an event, but rather that of a random variable. Probability distributions are determined by assigning an expectation to each random variable...
- Product distributionProduct distributionA product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions...
- Sum of normally distributed random variablesSum of normally distributed random variablesIn probability theory, calculation of the sum of normally distributed random variables is an instance of the arithmetic of random variables, which can be quite complex based on the probability distributions of the random variables involved and their relationships.-Independent random variables:If X...
- Slash distributionSlash distributionIn probability theory, the slash distribution is the probability distribution of a standard normal variate divided by an independent standard uniform variate...
- List of convolutions of probability distributions
-
