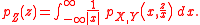A product distribution is a probability distribution

Probability distribution

In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....

 constructed as the distribution of the product

Product (business)

In general, the product is defined as a "thing produced by labor or effort" or the "result of an act or a process", and stems from the verb produce, from the Latin prōdūce ' lead or bring forth'. Since 1575, the word "product" has referred to anything produced...

 of random variable

Random variable

In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...

s having two other known distributions. Given two statistically independent random variables X and Y, the distribution of the random variable Z that is formed as the product

is a product distribution.

Algebra of random variables

The product is one type of algebra for random variables: Related to the product distribution are the ratio distribution

Ratio distribution

A ratio distribution is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions....

, sum distribution and difference distribution. More generally, one may talk of combinations of sums, differences, products and ratios.

Many of these distributions are described in Melvin D. Springer's book from 1979 The Algebra of Random Variables.

Derivation

A way of deriving the product distribution of Z from the joint distribution of the two other random variables, X and Y, is by integration of the following form

This is not always straightforward.

Special cases

The distribution of the product of two random variables which have lognormal distributions is again lognormal. This is itself a special case of a more general set of results where the logarithm of the product can be written as the sum of the logarithms. Thus, in cases where a simple result can be found in the list of convolutions of probability distributions, where the distributions to be convoluted are those of the logarithms of the components of the product, the result might be transformed to provide the distribution of the product. However this approach is only useful where the logarithms of the components of the product are in some standard families of distributions.

The distribution of the product of a random variable having a uniform distribution

Uniform distribution (continuous)

In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...

 on (0,1) with a random variable having a gamma distribution with shape parameter equal to 2, is an exponential distribution

Exponential distribution

In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...

. A more general case of this concerns the distribution of the product of a random variable having a beta distribution  with a random variable having a gamma distribution: for some cases where the parameters of the two component distributions are related in a certain way, the result is again a gamma distribution but with a changed shape parameter.

The K-distribution

K-distribution

The K-distribution is a probability distribution that arises as the consequence of a statistical or probabilistic model used in Synthetic Aperture Radar imagery...

is an example of a non-standard distribution that can be defined as a product distribution (where both components have a gamma distribution).