
Random binary tree
Encyclopedia
In computer science
and probability theory
, a random binary tree refers to a binary tree
selected at random from some probability distribution
on binary trees. Two different distributions are commonly used: binary trees formed by inserting nodes one at a time according to a random permutation
, and binary trees chosen from a uniform discrete distribution in which all distinct trees are equally likely. It is also possible to form other distributions, for instance by repeated splitting. Adding and removing nodes directly in a random binary tree will in general disrupt its random structure, but the treap
and related randomized binary search tree data structure
s use the principle of binary trees formed from a random permutation in order to maintain a balanced binary search tree dynamically as nodes are inserted and deleted.
For random trees that are not necessarily binary, see random tree
.
), one may form a binary search tree
in which each number is inserted in sequence as a leaf of the tree, without changing the structure of the previously inserted numbers. The position into which each number should be inserted is uniquely determined by a binary search in the tree formed by the previous numbers. For instance, if the three numbers (1,3,2) are inserted into a tree in that sequence, the number 1 will sit at the root of the tree, the number 3 will be placed as its right child, and the number 2 as the left child of the number 3. There are six different permutations of the numbers (1,2,3), but only five trees may be constructed from them. That is because the permutations (2,1,3) and (2,3,1) form the same tree.
of the length of the path from the root of the tree to is at most , where "" denotes the natural logarithm
function and the introduces big O notation
. For, the expected number of ancestors of is by linearity of expectation equal to the sum, over all other values in the set, of the probability that is an ancestor of . And a value is an ancestor of exactly when is the first element to be inserted from the elements in the interval . Thus, the values that are adjacent to in the sorted sequence of values have probability of being an ancestor of , the values one step away have probability , etc. Adding these probabilities for all positions in the sorted sequence gives twice a Harmonic number, leading to the bound above. A bound of this form holds also for the expected search length of a path to a fixed value that is not part of the given set.
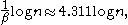
where is the unique number in the range satisfying the equation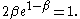
If a given set of ordered numbers is assigned numeric priorities (distinct numbers unrelated to their values), these priorities may be used to construct a Cartesian tree
for the numbers, a binary tree that has as its inorder traversal sequence the sorted sequence of the numbers and that is heap-ordered
by priorities. Although more efficient construction algorithms are known, it is helpful to think of a Cartesian tree as being constructed by inserting the given numbers into a binary search tree in priority order. Thus, by choosing the priorities either to be a set of independent random real numbers in the unit interval, or by choosing them to be a random permutation of the numbers from to (where is the number of nodes in the tree), and by maintaining the heap ordering property using tree rotation
s after any insertion or deletion of a node, it is possible to maintain a data structure that behaves like a random binary search tree. Such a data structure is known as a treap
or a randomized binary search tree.
: for these numbers of trees are
Thus, if one of these trees is selected uniformly at random, its probability is the reciprocal
of a Catalan number. Trees in this model have expected depth proportional to the square root of , rather than to the logarithm; however, the Strahler number
of a uniformly random binary tree, a more sensitive measure of the distance from a leaf in which a node has Strahler number whenever it has either a child with that number or two children with number , is with high probability logarithmic.
Due to their large heights, this model of equiprobable random trees is not generally used for binary search trees, but it has been applied to problems of modeling the parse tree
s of algebraic expressions
in compiler
design (where the above-mentioned bound on Strahler number translates into the number of registers
needed to evaluate an expression) and for modeling evolutionary trees. In some cases the analysis of random binary trees under the random permutation model can be automatically transferred to the uniform model.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
and probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a random binary tree refers to a binary tree
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
selected at random from some probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
on binary trees. Two different distributions are commonly used: binary trees formed by inserting nodes one at a time according to a random permutation
Random permutation
A random permutation is a random ordering of a set of objects, that is, a permutation-valued random variable. The use of random permutations is often fundamental to fields that use randomized algorithms such as coding theory, cryptography, and simulation...
, and binary trees chosen from a uniform discrete distribution in which all distinct trees are equally likely. It is also possible to form other distributions, for instance by repeated splitting. Adding and removing nodes directly in a random binary tree will in general disrupt its random structure, but the treap
Treap
In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys...
and related randomized binary search tree data structure
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
s use the principle of binary trees formed from a random permutation in order to maintain a balanced binary search tree dynamically as nodes are inserted and deleted.
For random trees that are not necessarily binary, see random tree
Random tree
In mathematics and computer science, a random tree is a tree or arborescence that is formed by a stochastic process. Types of random trees include:...
.
Binary trees from random permutations
For any set of numbers (or, more generally, values from some total orderTotal order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
), one may form a binary search tree
Binary search tree
In computer science, a binary search tree , which may sometimes also be called an ordered or sorted binary tree, is a node-based binary tree data structurewhich has the following properties:...
in which each number is inserted in sequence as a leaf of the tree, without changing the structure of the previously inserted numbers. The position into which each number should be inserted is uniquely determined by a binary search in the tree formed by the previous numbers. For instance, if the three numbers (1,3,2) are inserted into a tree in that sequence, the number 1 will sit at the root of the tree, the number 3 will be placed as its right child, and the number 2 as the left child of the number 3. There are six different permutations of the numbers (1,2,3), but only five trees may be constructed from them. That is because the permutations (2,1,3) and (2,3,1) form the same tree.
Expected depth of a node
For any fixed choice of a value in the given set of numbers, if one randomly permutes the numbers and forms a binary tree from them as described above, the expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the length of the path from the root of the tree to is at most , where "" denotes the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
function and the introduces big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
. For, the expected number of ancestors of is by linearity of expectation equal to the sum, over all other values in the set, of the probability that is an ancestor of . And a value is an ancestor of exactly when is the first element to be inserted from the elements in the interval . Thus, the values that are adjacent to in the sorted sequence of values have probability of being an ancestor of , the values one step away have probability , etc. Adding these probabilities for all positions in the sorted sequence gives twice a Harmonic number, leading to the bound above. A bound of this form holds also for the expected search length of a path to a fixed value that is not part of the given set.
The longest path
Although not as easy to analyze as the average path length, there has also been much research on determining the expectation (or high probability bounds) of the length of the longest path in a binary search tree generated from a random insertion order. It is now known that this length, for a tree with nodes, is almost surely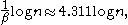
where is the unique number in the range satisfying the equation
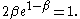
Expected number of leaves
In the random permutation model, each of the numbers from the set of numbers used to form the tree, except for the smallest and largest of the numbers, has probability of being a leaf in the tree, for it is a leaf when it inserted after its two neighbors, and any of the six permutations of these two neighbors and it are equally likely. By similar reasoning, the smallest and largest of the numbers have probability of being a leaf. Therefore, the expected number of leaves is the sum of these probabilities, which for is exactly .Treaps and randomized binary search trees
In applications of binary search tree data structures, it is rare for the values in the tree to be inserted without deletion in a random order, limiting the direct applications of random binary trees. However, algorithm designers have devised data structures that allow insertions and deletions to be performed in a binary search tree, at each step maintaining as an invariant the property that the shape of the tree is a random variable with the same distribution as a random binary search tree.If a given set of ordered numbers is assigned numeric priorities (distinct numbers unrelated to their values), these priorities may be used to construct a Cartesian tree
Cartesian tree
In computer science, a Cartesian tree is a binary tree derived from a sequence of numbers; it can be uniquely defined from the properties that it is heap-ordered and that a symmetric traversal of the tree returns the original sequence...
for the numbers, a binary tree that has as its inorder traversal sequence the sorted sequence of the numbers and that is heap-ordered
Binary heap
A binary heap is a heap data structure created using a binary tree. It can be seen as a binary tree with two additional constraints:*The shape property: the tree is a complete binary tree; that is, all levels of the tree, except possibly the last one are fully filled, and, if the last level of...
by priorities. Although more efficient construction algorithms are known, it is helpful to think of a Cartesian tree as being constructed by inserting the given numbers into a binary search tree in priority order. Thus, by choosing the priorities either to be a set of independent random real numbers in the unit interval, or by choosing them to be a random permutation of the numbers from to (where is the number of nodes in the tree), and by maintaining the heap ordering property using tree rotation
Tree rotation
A tree rotation is an operation on a binary tree that changes the structure without interfering with the order of the elements. A tree rotation moves one node up in the tree and one node down...
s after any insertion or deletion of a node, it is possible to maintain a data structure that behaves like a random binary search tree. Such a data structure is known as a treap
Treap
In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys...
or a randomized binary search tree.
Uniformly random binary trees
The number of binary trees with n nodes is a Catalan numberCatalan number
In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...
: for these numbers of trees are
- .
Thus, if one of these trees is selected uniformly at random, its probability is the reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of a Catalan number. Trees in this model have expected depth proportional to the square root of , rather than to the logarithm; however, the Strahler number
Strahler number
In mathematics, the Strahler number or Horton–Strahler number of a mathematical tree is a numerical measure of its branching complexity....
of a uniformly random binary tree, a more sensitive measure of the distance from a leaf in which a node has Strahler number whenever it has either a child with that number or two children with number , is with high probability logarithmic.
Due to their large heights, this model of equiprobable random trees is not generally used for binary search trees, but it has been applied to problems of modeling the parse tree
Parse tree
A concrete syntax tree or parse tree or parsing treeis an ordered, rooted tree that represents the syntactic structure of a string according to some formal grammar. In a parse tree, the interior nodes are labeled by non-terminals of the grammar, while the leaf nodes are labeled by terminals of the...
s of algebraic expressions
Expression (mathematics)
In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
in compiler
Compiler
A compiler is a computer program that transforms source code written in a programming language into another computer language...
design (where the above-mentioned bound on Strahler number translates into the number of registers
Register allocation
In compiler optimization, register allocation is the process of assigning a large number of target program variables onto a small number of CPU registers...
needed to evaluate an expression) and for modeling evolutionary trees. In some cases the analysis of random binary trees under the random permutation model can be automatically transferred to the uniform model.

