Treap
Encyclopedia
In computer science
, the treap and the randomized binary search tree are two closely related forms of binary search tree
data structure
s that maintain a dynamic set of ordered keys and allow binary searches among the keys. After any sequence of insertions and deletions of keys, the shape of the tree is a random variable
with the same probability distribution as a random binary tree
; in particular, with high probability its height is proportional to the logarithm
of the number of keys, so that each search, insertion, or deletion operation takes logarithmic time to perform.
and Raimund Seidel
in 1989; its name is a portmanteau
of tree and heap
.
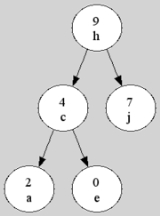
It is a Cartesian tree
in which each key is given a (randomly chosen) numeric priority. As with any binary search tree, the inorder traversal order of the nodes is the same as the sorted order of the keys. The structure of the tree is determined by the requirement that it be heap-ordered: that is, the priority number for any non-leaf node must be greater than or equal to the priority of its children. Thus, as with Cartesian trees more generally, the root node is the maximum-priority node, and its left and right subtrees are formed in the same manner from the subsequences of the sorted order to the left and right of that node.
An equivalent way of describing the treap is that it could be formed by inserting the nodes highest-priority-first into a binary search tree without doing any rebalancing. Therefore, if the priorities are independent random numbers (from a distribution over a large enough space of possible priorities to ensure that two nodes are very unlikely to have the same priority) then the shape of a treap has the same probability distribution as the shape of a random binary search tree, a search tree formed by inserting the nodes without rebalancing in a randomly chosen insertion order. Because random binary search trees are known to have logarithmic height with high probability, the same is true for treaps.
Specifically, the treap supports the following operations:
Aragon and Seidel also suggest assigning higher priorities to frequently accessed nodes, for instance by a process that, on each access, chooses a random number and replaces the priority of the node with that number if it is higher than the previous priority. This modification would cause the tree to lose its random shape; instead, frequently accessed nodes would be more likely to be near the root of the tree, causing searches for them to be faster.
Blelloch and Reid-Miller describe an application of treaps to a problem of maintaining set
s of items and performing set union, set intersection, and set difference operations, using a treap to represent each set. Naor and Nissim describe another application, for maintaining authorization certificates
in public-key cryptosystems
.
Rather than storing random priorities on each node, the randomized binary search tree stores at each node a small integer, the number of its descendants (counting itself as one); these numbers may be maintained during tree rotation operations at only a constant additional amount of time per rotation. When a key x is to be inserted into a tree that already has n nodes, the insertion algorithm chooses with probability 1/(n + 1) to place x as the new root of the tree, and otherwise it calls the insertion procedure recursively to insert x within the left or right subtree (depending on whether its key is less than or greater than the root). The numbers of descendants are used by the algorithm to calculate the necessary probabilities for the random choices at each step. Placing x at the root of a subtree may be performed either as in the treap by inserting it at a leaf and then rotating it upwards, or by an alternative algorithm described by Martínez and Roura that splits the subtree into two pieces to be used as the left and right children of the new node.
The deletion procedure for a randomized binary search tree uses the same information per node as the insertion procedure, and like the insertion procedure it makes a sequence of O(log n) random decisions in order to join the two subtrees descending from the left and right children of the deleted node into a single tree. If the left or right subtree of the node to be deleted is empty, the join operation is trivial; otherwise, the left or right child of the deleted node is selected as the new subtree root with probability proportional to its number of descendants, and the join proceeds recursively.
Although the treap and the randomized binary search tree both have the same random distribution of tree shapes after each update, the history of modifications to the trees performed by these two data structures over a sequence of insertion and deletion operations may be different. For instance, in a treap, if the three numbers 1, 2, and 3 are inserted in the order 1, 3, 2, and then the number 2 is deleted, the remaining two nodes will have the same parent-child relationship that they did prior to the insertion of the middle number. In a randomized binary search tree, the tree after the deletion is equally likely to be either of the two possible trees on its two nodes, independently of what the tree looked like prior to the insertion of the middle number.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, the treap and the randomized binary search tree are two closely related forms of binary search tree
Binary search tree
In computer science, a binary search tree , which may sometimes also be called an ordered or sorted binary tree, is a node-based binary tree data structurewhich has the following properties:...
data structure
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
s that maintain a dynamic set of ordered keys and allow binary searches among the keys. After any sequence of insertions and deletions of keys, the shape of the tree is a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with the same probability distribution as a random binary tree
Random binary tree
In computer science and probability theory, a random binary tree refers to a binary tree selected at random from some probability distribution on binary trees...
; in particular, with high probability its height is proportional to the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of the number of keys, so that each search, insertion, or deletion operation takes logarithmic time to perform.
Treap
The treap was first described by Cecilia R. AragonCecilia R. Aragon
Cecilia R. Aragon is an American computer scientist, professor, and championaerobatic pilot.In computer science, she is best known as the co-inventor of the treap data structure, a type of binary search tree that orders nodes by adding a priority as well as a key to each node...
and Raimund Seidel
Raimund Seidel
Raimund G. Seidel is a professor of computer scientist at the Universität des Saarlandes and an expert in computational geometry.Seidel was born in Graz, Austria, and studied with Hermann Maurer at the Graz University of Technology. He received his Ph.D. in 1987 from Cornell University under the...
in 1989; its name is a portmanteau
Portmanteau word
A portmanteau or portmanteau word is a blend of two words or morphemes into one new word. A portmanteau word typically combines both sounds and meanings, as in smog, coined by blending smoke and fog. More generally, it may refer to any term or phrase that combines two or more meanings...
of tree and heap
Heap (data structure)
In computer science, a heap is a specialized tree-based data structure that satisfies the heap property: if B is a child node of A, then key ≥ key. This implies that an element with the greatest key is always in the root node, and so such a heap is sometimes called a max-heap...
.
It is a Cartesian tree
Cartesian tree
In computer science, a Cartesian tree is a binary tree derived from a sequence of numbers; it can be uniquely defined from the properties that it is heap-ordered and that a symmetric traversal of the tree returns the original sequence...
in which each key is given a (randomly chosen) numeric priority. As with any binary search tree, the inorder traversal order of the nodes is the same as the sorted order of the keys. The structure of the tree is determined by the requirement that it be heap-ordered: that is, the priority number for any non-leaf node must be greater than or equal to the priority of its children. Thus, as with Cartesian trees more generally, the root node is the maximum-priority node, and its left and right subtrees are formed in the same manner from the subsequences of the sorted order to the left and right of that node.
An equivalent way of describing the treap is that it could be formed by inserting the nodes highest-priority-first into a binary search tree without doing any rebalancing. Therefore, if the priorities are independent random numbers (from a distribution over a large enough space of possible priorities to ensure that two nodes are very unlikely to have the same priority) then the shape of a treap has the same probability distribution as the shape of a random binary search tree, a search tree formed by inserting the nodes without rebalancing in a randomly chosen insertion order. Because random binary search trees are known to have logarithmic height with high probability, the same is true for treaps.
Specifically, the treap supports the following operations:
- To search for a given key value, apply a standard binary search algorithmBinary search algorithmIn computer science, a binary search or half-interval search algorithm finds the position of a specified value within a sorted array. At each stage, the algorithm compares the input key value with the key value of the middle element of the array. If the keys match, then a matching element has been...
in a binary search tree, ignoring the priorities. - To insert a new key x into the treap, generate a random priority y for x. Binary search for x in the tree, and create a new node at the leaf position where the binary search determines a node for x should exist. Then, as long as x is not the root of the tree and has a larger priority number than its parent z, perform a tree rotationTree rotationA tree rotation is an operation on a binary tree that changes the structure without interfering with the order of the elements. A tree rotation moves one node up in the tree and one node down...
that reverses the parent-child relation between x and z. - To delete a node x from the treap, if x is a leaf of the tree, simply remove it. If x has a single child z, remove x from the tree and make z be the child of the parent of x (or make z the root of the tree if x had no parent). Finally, if x has two children, swap its position in the tree with the position of its immediate successor z in the sorted order, resulting in one of the previous cases. In this final case, the swap may violate the heap-ordering property for z, so additional rotations may need to be performed to restore this property.
- To split a treap into two smaller treaps, those smaller than key x, and those larger than key x, insert x into the treap with maximum priority—larger than the priority of any node in the treap. After this insertion, x will be the root node of the treap, all values less than x will be found in the left subtreap, and all values greater than x will be found in the right subtreap. This costs as much as a single insertion into the treap.
- Merging two treaps (assumed to be the product of a former split), one can safely assume that the greatest value in the first treap is less than the smallest value in the second treap. Insert a value x, such that x is larger than this max-value in the first treap, and smaller than the min-value in the second treap, and assign it the minimum priority. After insertion it will be a leaf node, and can easily be deleted. The result is one treap merged from the two original treaps. This is effectively "undoing" a split, and costs the same.
Aragon and Seidel also suggest assigning higher priorities to frequently accessed nodes, for instance by a process that, on each access, chooses a random number and replaces the priority of the node with that number if it is higher than the previous priority. This modification would cause the tree to lose its random shape; instead, frequently accessed nodes would be more likely to be near the root of the tree, causing searches for them to be faster.
Blelloch and Reid-Miller describe an application of treaps to a problem of maintaining set
Set (computer science)
In computer science, a set is an abstract data structure that can store certain values, without any particular order, and no repeated values. It is a computer implementation of the mathematical concept of a finite set...
s of items and performing set union, set intersection, and set difference operations, using a treap to represent each set. Naor and Nissim describe another application, for maintaining authorization certificates
Public key certificate
In cryptography, a public key certificate is an electronic document which uses a digital signature to bind a public key with an identity — information such as the name of a person or an organization, their address, and so forth...
in public-key cryptosystems
Public-key cryptography
Public-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...
.
Randomized binary search tree
The randomized binary search tree, introduced by Martínez and Roura subsequently to the work of Aragon and Seidel on treaps, stores the same nodes with the same random distribution of tree shape, but maintains different information within the nodes of the tree in order to maintain its randomized structure.Rather than storing random priorities on each node, the randomized binary search tree stores at each node a small integer, the number of its descendants (counting itself as one); these numbers may be maintained during tree rotation operations at only a constant additional amount of time per rotation. When a key x is to be inserted into a tree that already has n nodes, the insertion algorithm chooses with probability 1/(n + 1) to place x as the new root of the tree, and otherwise it calls the insertion procedure recursively to insert x within the left or right subtree (depending on whether its key is less than or greater than the root). The numbers of descendants are used by the algorithm to calculate the necessary probabilities for the random choices at each step. Placing x at the root of a subtree may be performed either as in the treap by inserting it at a leaf and then rotating it upwards, or by an alternative algorithm described by Martínez and Roura that splits the subtree into two pieces to be used as the left and right children of the new node.
The deletion procedure for a randomized binary search tree uses the same information per node as the insertion procedure, and like the insertion procedure it makes a sequence of O(log n) random decisions in order to join the two subtrees descending from the left and right children of the deleted node into a single tree. If the left or right subtree of the node to be deleted is empty, the join operation is trivial; otherwise, the left or right child of the deleted node is selected as the new subtree root with probability proportional to its number of descendants, and the join proceeds recursively.
Comparison
The information stored per node in the randomized binary tree is simpler than in a treap (a small integer rather than a high-precision random number), but it makes a greater number of calls to the random number generator (O(log n) calls per insertion or deletion rather than one call per insertion) and the insertion procedure is slightly more complicated due to the need to update the numbers of descendants per node. A minor technical difference is that, in a treap, there is a small probability of a collision (two keys getting the same priority), and in both cases there will be statistical differences between a true random number generator and the pseudo-random number generator typically used on digital computers. However, in any case the differences between the theoretical model of perfect random choices used to design the algorithm and the capabilities of actual random number generators are vanishingly small.Although the treap and the randomized binary search tree both have the same random distribution of tree shapes after each update, the history of modifications to the trees performed by these two data structures over a sequence of insertion and deletion operations may be different. For instance, in a treap, if the three numbers 1, 2, and 3 are inserted in the order 1, 3, 2, and then the number 2 is deleted, the remaining two nodes will have the same parent-child relationship that they did prior to the insertion of the middle number. In a randomized binary search tree, the tree after the deletion is equally likely to be either of the two possible trees on its two nodes, independently of what the tree looked like prior to the insertion of the middle number.
External links
- Collection of treap references and info by Cecilia Aragon
- Treap Applet by Kubo Kovac
- Animated treap
- Randomized binary search trees. Lecture notes from a course by Jeff Erickson at UIUC. Despite the title, this is primarily about treaps and skip listSkip listA skip list is a data structure for storing a sorted list of items using a hierarchy of linked lists that connect increasingly sparse subsequences of the items...
s; randomized binary search trees are mentioned only briefly. - A high performance key-value store based on treap by Junyi Sun
- VB6 implementation of treaps. Visual basic 6 implementation of treaps as a COM object.
- ActionScript3 implementation of a treap

