Gyration tensor
Encyclopedia
The gyration tensor is a tensor
that describes the second moment
s of position of a collection of particle
s
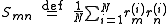
where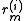
is the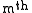 
Cartesian coordinate
of the position vector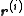
of the
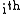particle. The origin
of the coordinate system
has been chosen such that
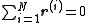
i.e. in the system of the center of mass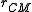
. Where
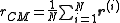
In the continuum limit,
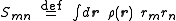
where
represents the number density of particles at position 
.
Although they have different units, the gyration tensor is related to the
moment of inertia tensor. The key difference is that the particle positions are weighted by mass
in the inertia tensor, whereas the gyration tensor depends only on the particle positions; mass plays no role in defining the gyration tensor. Thus, the gyration tensor would be proportional to the inertial tensor if all the particle masses were identical.
, a Cartesian coordinate system
can be found in which it is diagonal
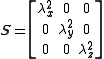
where the axes are chosen such that the diagonal elements are ordered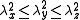
.
These diagonal elements are called the principal moments of the gyration tensor.
is the sum of the principal moments
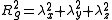
The asphericity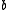
is defined by
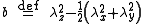
which is always non-negative and zero only when the three principal moments are equal, λx = λy = λz. This zero condition is met when the distribution of particles is spherically symmetric (hence the name asphericity) but also whenever the particle distribution is symmetric with respect to the three coordinate axes, e.g., when the particles are distributed uniformly on a cube
, tetrahedron
or other Platonic solid
.
Similarly, the acylindricity
is defined by
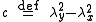
which is always non-negative and zero only when the two principal moments are equal, λx = λy.
This zero condition is met when the distribution of particles is cylindrically symmetric (hence the name, acylindricity), but also whenever the particle distribution is symmetric with respect to the two coordinate axes, e.g., when the particles are distributed uniformly on a regular prism
.
Finally, the relative shape anisotropy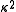
is defined
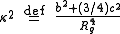
which is bounded between zero and one.
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
that describes the second moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
s of position of a collection of particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
s
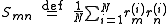
where
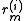is the Cartesian coordinate
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
of the position vector
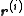of the 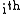particle. The originOrigin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
of the coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
has been chosen such that
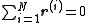
i.e. in the system of the center of mass
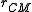. Where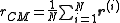In the continuum limit,
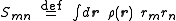
where
represents the number density of particles at position .Although they have different units, the gyration tensor is related to the
moment of inertia tensor. The key difference is that the particle positions are weighted by mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
in the inertia tensor, whereas the gyration tensor depends only on the particle positions; mass plays no role in defining the gyration tensor. Thus, the gyration tensor would be proportional to the inertial tensor if all the particle masses were identical.
Diagonalization
Since the gyration tensor is a symmetric 3x3 matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, a Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
can be found in which it is diagonal
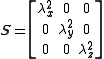
where the axes are chosen such that the diagonal elements are ordered
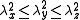.These diagonal elements are called the principal moments of the gyration tensor.
Shape descriptors
The principal moments can be combined to give several parameters that describe the distribution of particles. The squared radius of gyrationRadius of gyration
Radius of gyration or gyradius is the name of several related measures of the size of an object, a surface, or an ensemble of points. It is calculated as the root mean square distance of the objects' parts from either its center of gravity or an axis....
is the sum of the principal moments
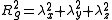
The asphericity
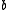is defined by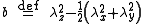which is always non-negative and zero only when the three principal moments are equal, λx = λy = λz. This zero condition is met when the distribution of particles is spherically symmetric (hence the name asphericity) but also whenever the particle distribution is symmetric with respect to the three coordinate axes, e.g., when the particles are distributed uniformly on a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
, tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
or other Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
.
Similarly, the acylindricity
is defined by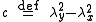which is always non-negative and zero only when the two principal moments are equal, λx = λy.
This zero condition is met when the distribution of particles is cylindrically symmetric (hence the name, acylindricity), but also whenever the particle distribution is symmetric with respect to the two coordinate axes, e.g., when the particles are distributed uniformly on a regular prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
.
Finally, the relative shape anisotropy
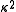is defined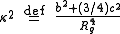which is bounded between zero and one.